En este artículo aplicaremos un algoritmo de regresión logística variando el valor de C.
Recordemos que la regresión logística es un proceso de modelado de la probabilidad de un
resultado discreto dada una variable de entrada.
La regresión logística más común nos trae como resultado un modelo binario, es decir, un modelo que puede tomar valores como verdadero o falso, sí o no, etc. La regresión logística multinomial o binomial puede modelar diversos resultados donde hay dos o más opciones posibles que se interpretan como resultados discretos.
La regresión logística se utilizó en las ciencias de la biología a principios del siglo XX. Luego se aplicó en muchas de las áreas de las ciencias sociales, como la antropología, la sociología o la psicología, donde es necesario tener en cuenta factores estadísticos.
Este tipo de regresión se utiliza cuando la variable dependiente o variable objetivo es categórica.
Algoritmo de regresión logística
#Algoritmo de regresión logística variando el valor de C
# Ejemplo 2
#preparamos los datos
data2 = ejemplo2.values
X2 = data2 [ : , 0 : 2]
y2 = data2 [ : , - 1]
#creamos el modelo
lr2= LogisticRegression() #C = 1.0 (valor por defecto)
#ajustamos con los datos disponibles
lr2.fit (x2, y2)
plot_decision_boundary (X2, y2, 0.05, lr2)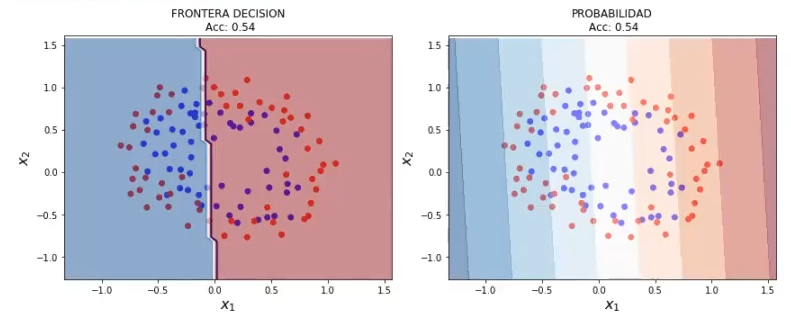
Vamos a crear un polynomialfeatures. Lo que hace esta función es generar características polinómicas, que básicamente consisten en: si tenemos x1, va a ser (x1)2 y lo va a meter como input. Si le decimos que en vez de ser grado 2 sea grado 5, va a coger (x1)2, (x1)3, (x1)4, (x1)5… y los va a meter a todos como inputs. De esta manera, lo que se consigue es que ya no obtengamos una línea recta, sino que puede ser capaz de detectar cosas más complejas.
El grado por defecto del polynomial features es 2, así que si lo vamos a dejar en ese valor, no es necesario ponerlo entre los paréntesis.
#Algoritmo de regresión logística variando el valor de C
poly = PolynomialFeatures ()
X2poly = poly.fit_transform (X2)
lr2 = LogisticRegression (C = 100000, solver = 'saga') # C = 1.0 (valor por defecto)
lr2.fit (X2poly, y2)
plot_decision_boundary_poly (X2, y2, 0.05, lr2, poly)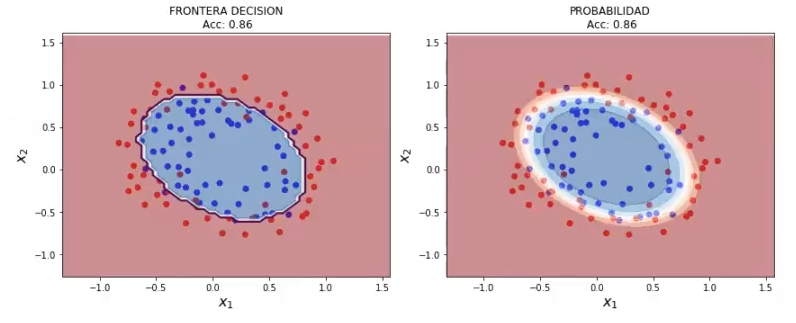
Aquí vemos cómo, con una regularización alta, en el momento en el que le metemos polynomial features, ya se pueden hacer otras cosas.
Pongamos otro valor en C, en este caso será 0.4, a ver qué pasa:
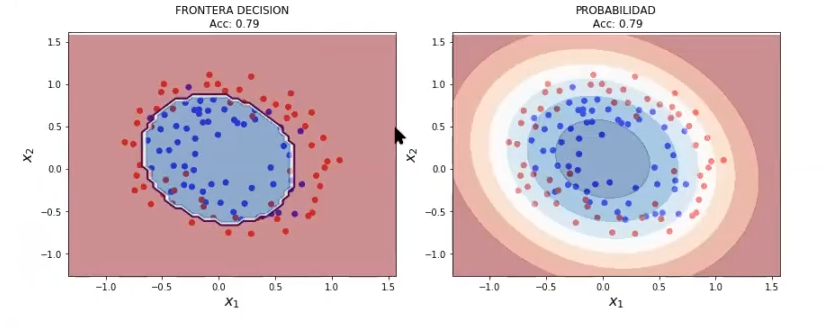
Si le ponemos regularización fuerte al algoritmo anterior, es decir, cambiamos el C por un C pequeño, de 1000 lo ponemos en 0.01, lo que va a pasar es que tenemos un modelo más simple, más sencillo de entender:
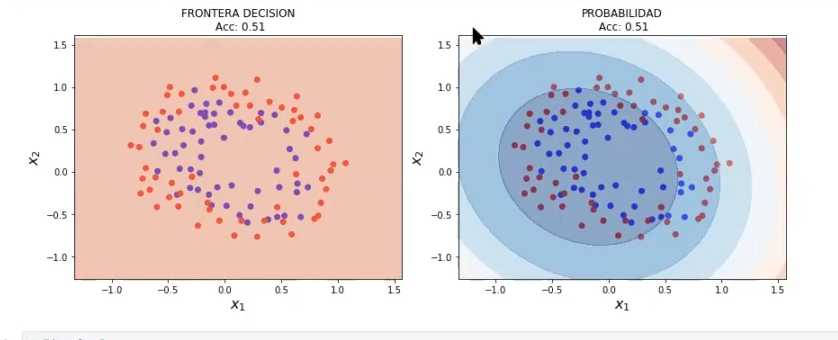
Ahora hagamos lo mismo con el ejemplo 3:
#Algoritmo de regresión logística variando el valor de C
#Ejemplo 3
#creamos el modelo
lr3= LogisticRegression() # C = 1.0 (valor por defecto)
#ajustamos con los datos disponibles
lr3.fit (X3, y3)
plot_decision_boundary (X3, y3, 0.05, lr3)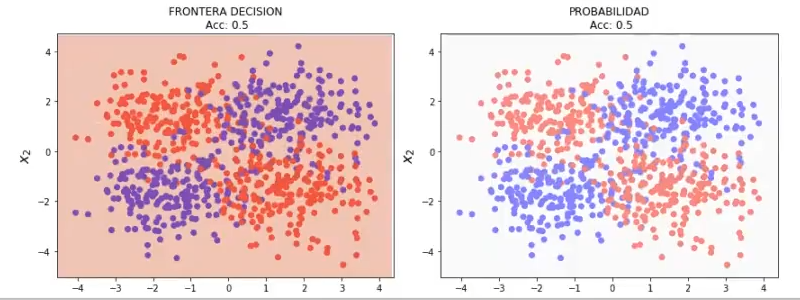
#Algoritmo de regresión logística variando el valor de C
poly3 = PolynomialFeatures (2)
X3poly = poly3.fit_transform (X3)
lr3 = LogisticRegression (C = 100000, solver = 'saga') # C = 1.0 (valor por defecto)
lr3.fit (X3poly, y3)
plot_decision_boundary_poly (X3, y3, 0.05, lr3, poly)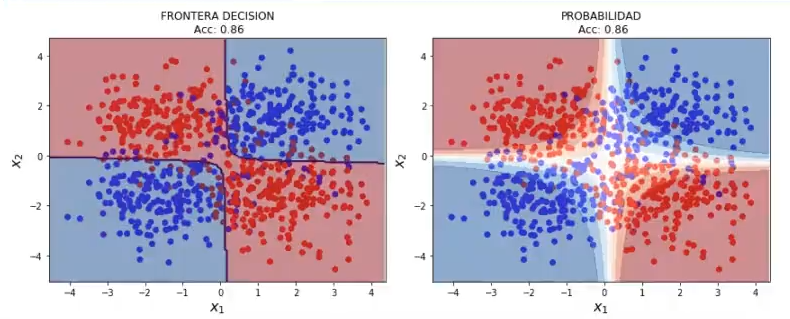
Ahora cambiemos la regularización:
#Algoritmo de regresión logística
lr3 = LogisticRegression (C = 0.00000002, solver = 'saga')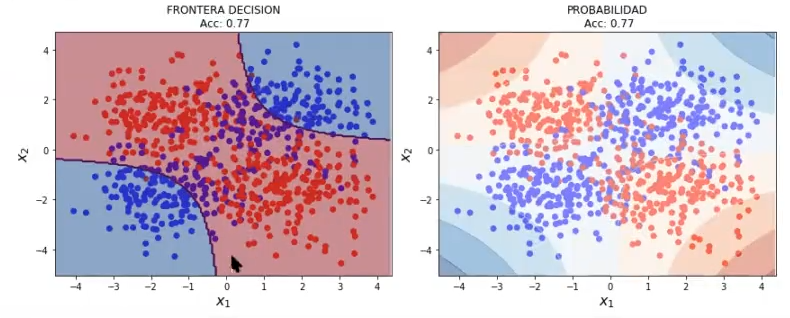
Este es un modelo muy simple. Vemos cómo es mucho menos exacto que con un modelo más regularizado.
Lo extraño de esto es que si dejamos la regularización por defecto, es decir el C = 1, no cambia prácticamente nada, se queda casi lo mismo que si le metemos una regularización prácticamente nula, muy pequeña (valores como 0.0000000000002).
Esto puede indicar que, por defecto, el algoritmo ya regulariza, y si se le quiere meter una regularización, hay que bajar bastante el valor de C para poder notarla:
#Algoritmo de regresión logística variando el valor de C
poly3 = PolynomialFeatures (2)
X3poly = poly3.fit_transform (X3)
lr3 = LogisticRegression (C = 0.0000001, solver = 'saga') # C = 1.0 (valor por defecto)
lr3.fit (X3poly, y3)
plot_decision_boundary_poly (X3, y3, 0.05, lr3, poly)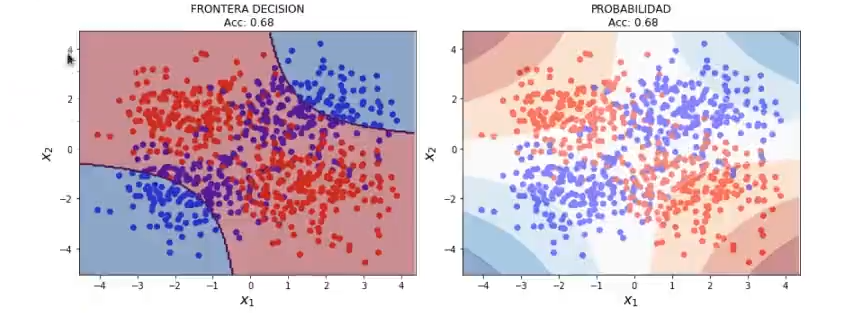
Si dejamos el grado del polynomial features en 2, el modelo no va a poder mejorar casi nada, debido a esta restricción.
Como hemos podido observar a lo largo de diferentes posts, existen muchos tipos de regresiones y otras tantas de implementarlas en diferentes ejercicios de Big Data. Si quieres seguir aprendiendo cómo usar las regresiones y entender otras temáticas relacionadas con este mundillo, te invitamos a inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que tendrás la oportunidad de adquirir toda la fundamentación teórica y práctica para incursionar en uno de los mercados laborales mejor pagados y más demandados de la actualidad. ¡Entra y solicita más información ahora!







