¿Sabes cómo ampliar una regresión lineal y para qué se usa este procedimiento?
Lo bueno de la regresión lineal y de los mínimos cuadrados es que son muy versátiles. Seguro que piensas que calcular una función lineal es un problema muy simple, teniendo en cuenta que solo estamos dibujando una línea a través de nuestro hiperplano, pero eso no es así. Las funciones lineales son la base de todo, incluso de las redes neuronales.
Ampliar una regresión lineal
Las regresiones lineales y los mínimos cuadrados son herramientas muy potentes. Recuerda que la regresión lineal se llama de este modo porque la salida es lineal:
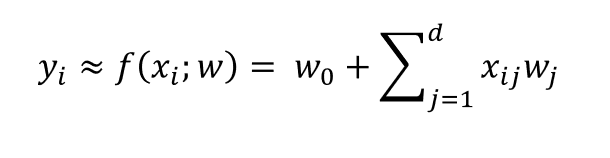
Aquí, como vemos, tenemos una relación lineal de los pesos w, no necesariamente de las entradas x. En el siguiente ejemplo, la regresión lineal va a ser algo que NO queramos utilizar, porque no va a modelar correctamente nuestros datos. ¿Qué hacemos entonces?
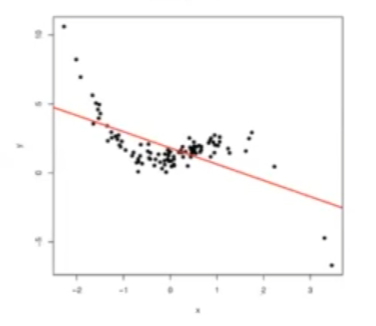
y = w0 + w1x
Si tenemos los datos de esta forma, estaríamos simplificando mucho el problema, es decir, que nuestro modelo, la hipótesis del mismo, no sería lo suficientemente compleja para poder representar bien nuestros datos. Por tanto, tenderíamos al underfitting, es decir, que nuestro modelo no aprendiese bien de los datos.
¿Cómo solucionamos esto? La solución más fácil es coger la ecuación presentada arriba y añadirle el cuadrado, es decir, el resultado de las operaciones hechas dentro de la misma, se tomará al cuadrado, pudiendo así ampliar una regresión lineal.
Ya sabemos que todas las ecuaciones polinómicas tienen la forma de x2 + x + b, donde B es un número y a x2 y x se les añade uno también.
Así pues, una forma de expresar estos datos que tienen una forma tan curiosa es extender la ecuación usando cuadrados.
Si miramos la ecuación original de la regresión lineal, tenemos la salida y, que es aproximadamente igual a la entrada x multiplicando por un peso w1, más un desplazamiento w0.
Básicamente, estamos diciendo que los datos tienen que ser modelados por una línea, pero no es lo ideal en este caso.
Podríamos decir ahora que nuestra salida y sea de la forma:
y = w0 + w1x + w2x2 + w3x3
Entonces, si miramos en la ecuación anterior, le añadimos a x2 un x3, con lo que aquí también se logró ampliar una regresión lineal y el resultado es el siguiente:
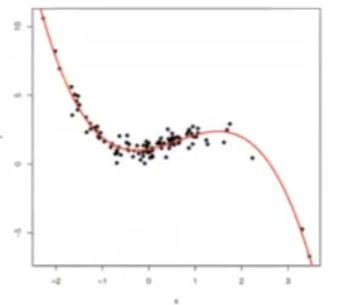
Esto es lo que se denomina regresión polinomial utilizando una función de 3 orden, con lo que ya podemos ampliar una regresión lineal. Lo mejor de todo es que se resuelve de la misma forma que la regresión lineal, usando:
XT XW’ = XT y
O lo que es lo mismo:
W’ = (XT X)-1 XT y
La única diferencia es que nuestra matriz X con un polinomio de grado p será de la forma:

Donde p será el orden de nuestro polinomio.
Nota: d = 1 indica que solo tiene una variable, por ejemplo: edad/dinero.
Influencia del grado del polinomio en nuestra regresión
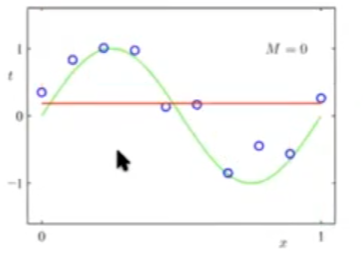
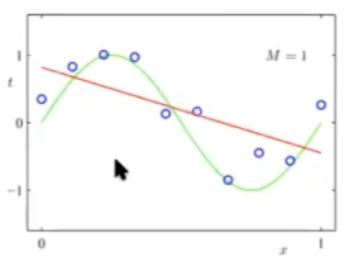
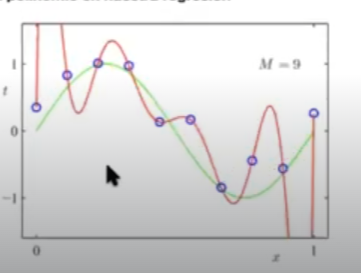
Regresión polinomial en R2 (2 dimensiones)
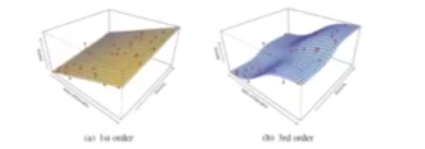
Como hemos visto, la regresión polinomial se resuelve de la misma forma que una regresión lineal, la única diferencia es que tendremos más componentes en nuestra matriz X. El número de columnas vendrá dado por:
(orden polinomio) x (dimensiones) + 1
En ese caso, para un polinomio de orden 2:
yi = w0 + w1xi1 + w2xi2 + w3x2 i1 + w4x2 i2
Para un polinomio de orden 3:
yi = w0 + w1xi1 + w2xi2 + w3x2 i1 + w4x2 i2 + w5x3 i1 + w6x3 i2
¿Quieres seguir avanzando en tu formación?
Ahora que hemos visto cómo ampliar una regresión lineal, podemos seguir aprendiendo otras cosas relacionadas con este campo. El Big Data es una de las áreas en las que más trabajos se ofertan. Para poder acceder a este tipo de opciones laborales, que son de las más prolíficas y mejor pagadas actualmente, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que adquirirás todos los conocimientos teóricos y prácticos que te acercarán al trabajo de tus sueños en pocos meses. ¡Anímate y solicita más información ahora!











