El análisis estadístico de dos variables dependientes es uno de los distintos estudios que te permiten esclarecer cómo son los datos que te encuentras trabajando a partir de un análisis conjunto, de ahí su importancia para saber cómo se comporta la población de los datos procesados.
Por esta razón, en este post, te explicamos cómo funciona el análisis estadístico de dos variables dependientes.
Análisis estadístico de dos variables dependientes
Para comprender cómo funciona el análisis estadístico de dos variables dependientes te exponemos el siguiente ejemplo:
En el que: P(B,A)=P(B|A)·P(A)=P(A,B)=P(A|B)·P(B).
En este caso la matriz de covarianza no es diagonal.
N<-10000
A<-rnorm(N,mean=0,sd=2)
B<-A+rnorm(N,mean=0,sd=2)
df<-data.frame(A,B)
print(paste("Matriz de covarianza:"))
cov(df)
library(ggplot2)
ggplot(df, aes(x=A, y=B))+geom_density2d(aes(colour=..level..)) +
stat_density2d(aes(fill=..level..,alpha=..level..),geom='polygon',colour='black') +
scale_fill_continuous(low="green",high="red") +
geom_point(alpha=0.1,size=0.1)+
theme_bw()+theme(legend.position="none")+xlim(c(-10,10))+ylim(c(-10,10))
En este análisis estadístico de dos variables dependientes, precisamente, como son dependientes, la probabilidad condicional de B respecto a A es diferente a la probabilidad de B, así:
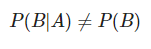
dfPartialProbs<-data.frame(B=B,var="P(B)") dfPartialProbs<-rbind(dfPartialProbs,data.frame(B=df$B[df$A>-0.5 & df$A<0.5],var="P(B|-0.5<A<0.5)")) dfPartialProbs<-rbind(dfPartialProbs,data.frame(B=df$B[df$A>3 & df$A<4],var="P(B|3<A<4)")) ggplot(dfPartialProbs, aes(x=B,color=var))+geom_density()+ theme_bw()

Dos variables independientes
A la par del análisis estadístico de dos variables dependientes, podrás encontrar el de las variables independientes, siguiendo el ejemplo: P(B,A)=P(B)·P(A).
A diferencia de las dependientes, su matriz de covarianza se parece a una matriz diagonal.
N<-10000
A<-rnorm(N,mean=0,sd=0.5)
B<-rnorm(N,mean=0,sd=1)
df<-data.frame(A,B)
print(paste("Matriz de covarianza:"))
cov(df)
library(ggplot2)
ggplot(df, aes(x=A, y=B))+geom_density2d(aes(colour=..level..)) +
stat_density2d(aes(fill=..level..,alpha=..level..),geom='polygon',colour='black') +
scale_fill_continuous(low="green",high="red") +
geom_point(alpha=0.2,size=0.1)+
theme_bw()+theme(legend.position="none")+xlim(c(-5,5))+ylim(c(-5,5))
Como son independientes, la probabilidad condicional de B respecto a A es igual a la probabilidad de B
P(B|A)=P(B)
dfPartialProbs<-data.frame(B=B,var="P(B)") dfPartialProbs<-rbind(dfPartialProbs,data.frame(B=df$B[df$A>-0.5 & df$A<0.5],var="P(B|-0.5<A<0.5)")) ggplot(dfPartialProbs, aes(x=B,color=var))+geom_density()+ theme_bw()
¿Quieres seguir aprendiendo del Big Data?
En este post, te hemos hablado sobre el análisis estadístico de dos variables dependientes, de manera que ahora podrás utilizarlo en el procesamiento de tus datos. No obstante, este es un amplio campo que requiere de muchos más estudios para tener mejores resultados.
Por este motivo, desde KeepCodging te presentamos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de alta calidad por medio de la que podrás aprender mucho más sobre este servicio y, en general, sobre los sistemas y herramientas más importantes en el mundo del Big Data.
De esta forma, de la mano de profesionales y en menos de nueve meses, te convertirás en todo un experto y podrás conocer e identificar las alternativas de gestión de datos más apropiadas para los estudios de los macrodatos. ¡No esperes más para empezar e inscríbete ahora!











