A continuación te explicaremos cómo aplicar PCA al reconocimiento facial por medio de un ejercicio con el que hemos trabajado en otros artículos del blog. Dicho ejercicio consiste en crear un algoritmo que determine si una imagen mostrada de un dataset de más de 5000 imágenes pertenece o no a la cara de George Bush.
Aplicar PCA al reconocimiento facial
Sobre la matriz de train podemos aplicarle PCA al reconocimiento facial. El resultado debería ser una matriz con 62500 autovectores de dimensión 62500. Sin embargo, dado que el número de fotos en training es de solo 947 (menor de 62500), los autovalores correspondientes a los autovectores desde 948 hasta 62500 son 0. Por ese motivo, solo habrá 947 autovectores de dimensión 62500.
Mejoras de R
Aquí estamos trabajando con matrices muy grandes y R, por defecto, es monohilo. El proceso del primer algoritmo ha tardado relativamente poco, pero para acelerar operaciones de álgebra lineal se pueden aprovechar las librerías BLAS. Las tenéis disponibles para:
- Windows.
- Linux/Mac.
- En sistemas tipo Debian basta con instalar la libreria libopenblas-dev: apt-get install libopenblas-dev.
Tenemos 62500 columnas. En una PCA la matriz de rotación era una matriz cuadrada y tenía el mismo número de filas que de columnas. Entonces, si tenemos aquí 62500, lo que vamos a tener es una matriz de 62500×62500. Eso, por supuesto, no va a ocurrir, porque tenemos solo 947 muestras. El resto de elementos, a partir de 947, se van a calcular, pero van a ser 0. Por este motivo, no nos los va a mostrar.
#Aplicar PCA al reconocimiento facial pr_pics <- prcomp (train_matrix, center = TRUE, scale. = TRUE)
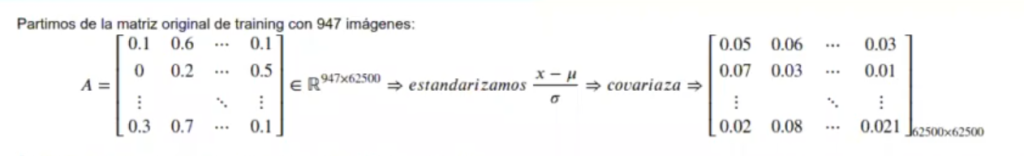
La que se muestra es la matriz de entrenamiento o training, que contiene 947 filas y 62500 columnas. ¿Qué hacemos? Estandarizamos por medio del center = TRUE y el scale = TRUE.
¡Imagina la matriz tan grande que ha tenido que calcular! 62500×62500 son muchos datos.
Calculamos los autovectores y autovalores de la matriz de covarianza.
Tendremos 62500 autovalores:
λ = [118 59.6 55.8 … 1 0.9 le – 14 0 … 0]1×62500
De los cuales solo los 947 primeros tendrán un valor superior a 0, por lo que podemos simplificarlo como:
λ = [118 59.6 55.8 … 1 0.9 le – 14]x947
Si tenemos 947 autovalores no nulos, solo necesitaremos los correspondientes 947 autovectores.
No obstante, hay que tener en cuenta que estos valores van a empezar a bajar, primero está 118, luego está 59.6 y así sucesivamente. A partir de la posición 947, aquí ya sale en 0.
De modo que, si tenemos 947 autovalores no nulos, solo necesitamos para la matriz de rotación 947 componentes principales o autovectores.
No olvides que el número de filas que tiene cada autovector sigue siendo 62500, porque en la matriz original hay 62500 columnas. Entonces, recordemos que, para poder hacer la transformación, cada columna va a tener que ir multiplicada por uno de los valores de ese autovector.
Por eso va a haber 62500 filas y solo 947 columnas. Como no hay más valores, es decir, más fotos, el resto de columnas son 0. Si tuviéramos más fotos, por ejemplo 1000, el número al final de la ecuación λ = [118 59.6 55.8 … 1 0.9 le – 14]x947 en vez de ser 947 sería 1000.

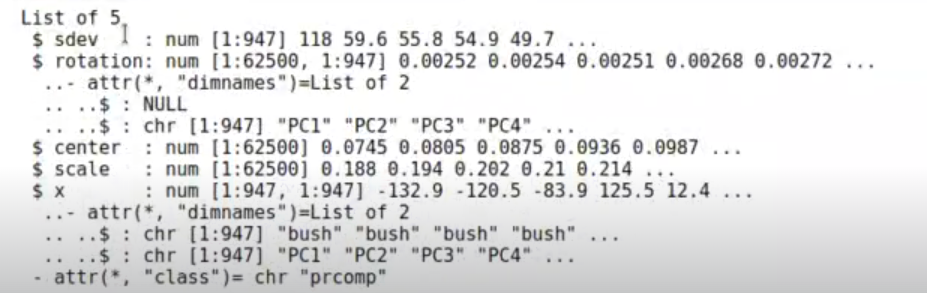
El que se muestra a continuación es el modelo que nos ha dado del prcomp. Vemos en el resultado la desviación típica. Ahí aparece todo lo que ya hemos explicado anteriormente.
Recordemos que la matriz A la tendremos que multiplicar por la matriz V, esto significa que multiplicamos filas por columnas.
#Aplicar PCA al reconocimiento facial str(pr_pics)
Tenemos, a continuación, la matriz de autovalores. Sacamos los diez primeros valores:
#Aplicar PCA al reconocimiento facial #Matriz de autovalores pr pics$sdev [1:10]

Para la matriz de autovectores, sacamos 5 filas al azar y los 10 primeros autovectores.
#Aplicar PCA al reconocimiento facial #Matriz de autovectores pr_pics$rotation [sample (1 : nrow (pr_pics$rotation), 5), 1 : 10]
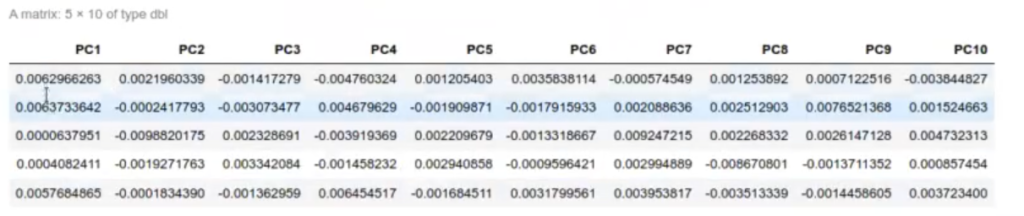
Lo más importante de todo esto es la matriz de rotación, es decir, la matriz con el valor V.
Ahora que hemos aprendido a aplicar PCA al reconocimiento facial por medio de nuestro algoritmo de Eigenfaces, quizás te interese leer nuestro artículo «Aplicar PCA al dataset de proteínas«.
Por último, debes saber que puedes seguir aprendiendo por medio del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp que tenemos para ti. Este bootcamp consiste en una formación intensiva en la que adquirirás todos los conocimientos necesarios a nivel teórico y práctico para incursionar en el mercado laboral. ¡Anímate a dar el paso que cambiará tu vida y solicita ahora más información!











