¿Sabes por qué es necesario aplicar validación cruzada en un ejercicio de sesgo-varianza? En este artículo te contaremos el motivo, pero, antes, recordemos que el compromiso sesgo-varianza es un principio que nos permite analizar el alcance de las prestaciones en tareas de aprendizaje supervisado.
Asimismo, la validación cruzada o cross validation es un método que se utiliza para estimar las métricas de rendimiento y precisión en el entrenamiento de un modelo de machine learning y para prevenir overfittings.
Aplicar validación cruzada en un ejercicio de sesgo-varianza
Para aplicar validación cruzada en un ejercicio de sesgo-varianza resolveremos un ejercicio en el que calcularemos las prestaciones de distintos modelos y conjuntos de entrenamiento y, posteriormente, su media y su varianza.
#aplicar validación cruzada en un ejercicio de sesgo-varianza
import warnings
warnings.filterwarnings ("ignore")
N=10
grado polinomio = [1, 4, 7]
Nrepeticiones = 20
#inicializamos
mse = np.zeros ((len (grado_polinomio), Nrepeticiones))
f_w = np.zeros ((Nrepeticiones, N_test, len (grado_polinomio)))
np.random.seed (0)
plt.figure (figsize = (14, 5))
for k in range (Nrepeticiones):
y=g_x + np.random.randn (N_test) * 0.2
#Obtén las muestras de un nuevo conjunto de entrenamiento
#aplicar validación cruzada en un ejercicio de sesgo-varianza
idx = np.random.randint (0, N_test, N_train)
x_i = x [idx]
y_i = y [idx]
for j, d in enumerate (grado_polinomio):
f_k, mse [j, kl, miRegresionLineal (x_i, y_i, x, y, d)
f_w [k, : , j] = f_k
ax = plt.subplot (1, 3, j + 1)
plt.plot (x_i, y_i, 'b.', alpha = 0.1)
plt.plot(x, f_k, 'g', alpha = 0.1)
for j, d in enumerate (grado_polinomio):
ax1 = plt.subplot (1, 3, j + 1)
f_k = np.mean (f_w [ : , : , j ].axis = 0)
bias = g_x - f_k
var = np.var [f_w [ : , : , j ].axis = 0)
plt.setp (ax, xticks = (), yticks = ())
plt.plot (x, g_x, 'r')
plt.plot (x, f_k, 'g', linewidth = 2)
plt.title ('Grado: %i nMSE: %.2f +/- %.2f nBIAS: %.2f VAR: %.2f' % (d,
np.mean (mse [ j, : ],
np.std [mse [ j , :]),
np.mean (bias ** 2).
np.mean (var)))
plt.ylim (-2, 2))
plt.xlim ((0, 1))
plt.show ()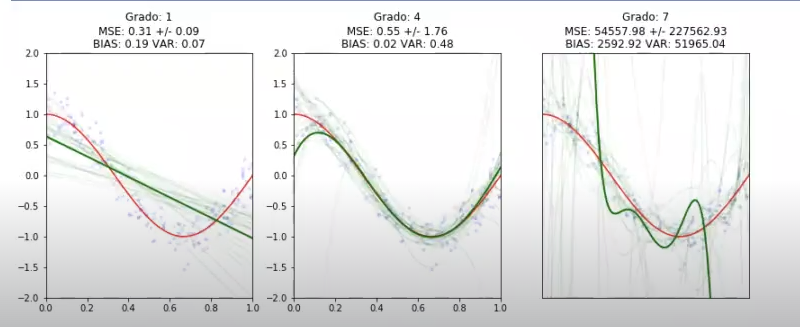
Esto lo que hace es ejecutar nuestro algoritmo un montón de veces; en este caso son 20, ya que dijimos que Nrepeticiones era igual a 20, con Grado 1, con Grado 4 y con Grado 7. En la primera gráfica, podemos observar una media de todos los valores que hay.
También vemos cómo, si hacemos la media en 20 iteraciones, el modelo que mejor se ajusta es, sin duda alguna, el modelo de Grado 4. El peor es el de Grado 7 y luego está el de Grado 1, que se queda un poco corto al tratarse de una recta.
¿Por qué es importante hacer esto de aplicar validación cruzada en un ejercicio de sesgo-varianza? Pues porque podría darse el caso de que, para determinado conjunto de instancias, el Grado 3 y el Grado 7 fueran prácticamente similares, o que incluso el Grado 7 fuera ligeramente mejor. Observemos el ejemplo siguiente:
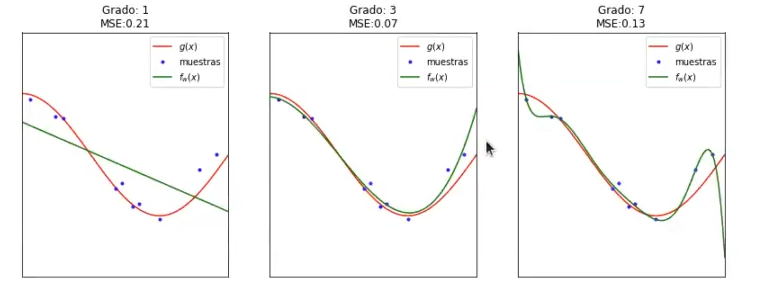
En estos últimos modelos tenemos un error cuadrático medio de 0.07 y 0.13, que no están tan lejos. Si viéramos este conjunto de entrenamiento, a lo mejor podríamos decir que el Grado 7 es el que nos sirve y es el mejor, pero si observamos las diferentes iteraciones nos damos cuenta de que no es así:
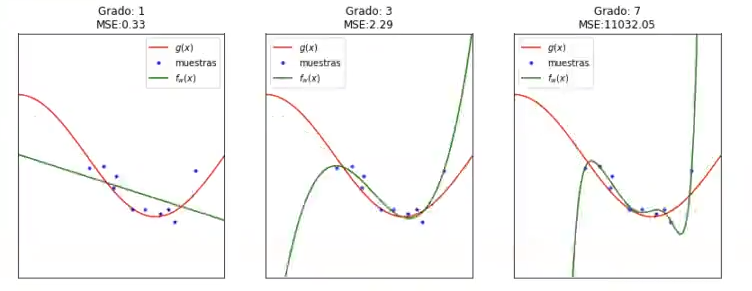
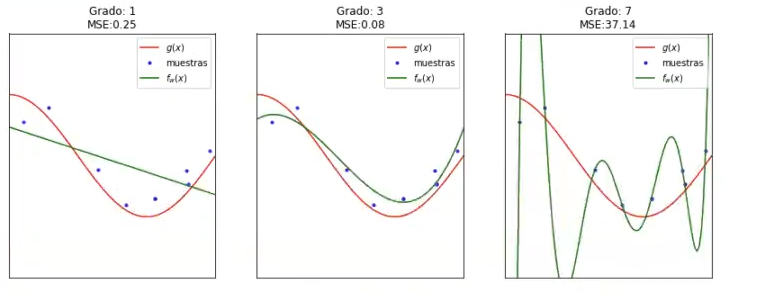
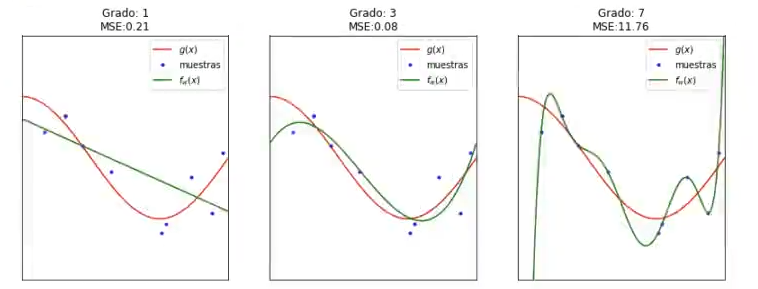
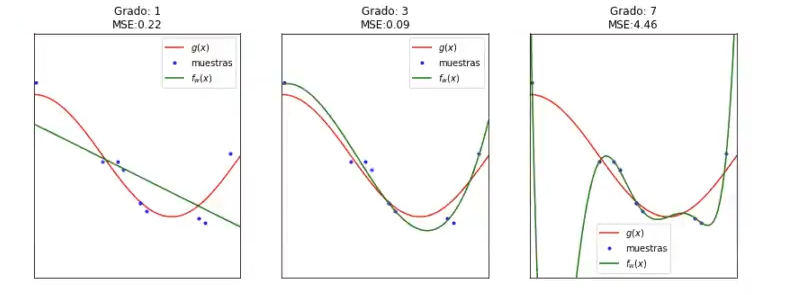
Por eso, es importante hacer algo que reduzca esa varianza, que reduzca esa dependencia de los datos de entrenamiento. Ese algo es el cross validation. Aplicar validación cruzada a un ejercicio de sesgo-varianza es la mejor opción y es precisamente lo que estamos haciendo aquí. Entrenamos con varios conjuntos de entrenamiento y calculamos una media.
En alguno de los casos queda un conjunto de datos diferente, como en el caso de la iteración 6, en la que el Grado 7 es casi igual que el Grado 3, la media va a ser que el Grado 7 es mucho peor que el Grado 3.
Así pues, hemos visto cómo de necesario es aplicar validación cruzada en un ejercicio de sesgo-varianza para poder reducir la posibilidad de algún error fatal de confusión.
Si quieres seguir aprendiendo más sobre temáticas como esta, relacionadas con el Big Data y todas sus sus áreas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que podrás adquirir todas las herramientas teóricas y prácticas y poner a prueba tus conocimientos para incursionar rápidamente en un mercado laboral lleno de oportunidades. ¡No esperes para solicitar más información y seguir forjando tu camino hacia el éxito!



