En este post te enseñaremos cómo obtener un AUC más alto separando las curvas de densidad.
En un artículo anterior habíamos realizado un ejercicio de machine learning que consistía en buscar la proyección que mejor nos permitía separar dos clases de interés: el LDA y el PCA. Para ello, habíamos buscado la forma de calcular el análisis discriminante lineal y, al final, obtuvimos una recta en la que se mostraban todos los datos en forma de puntos y su respectiva distribución, así como la gráfica de distribución en la que podíamos notar que en cierta parte se tocaban ambos lados.
Lo que queremos hacer en este caso es obtener una curva AUC más precisa.
AUC más alto separando las curvas de densidad
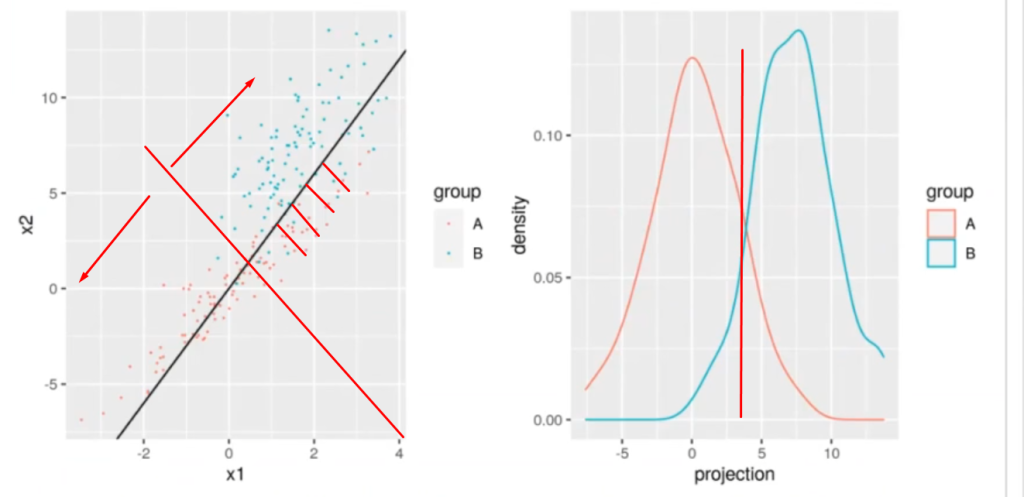
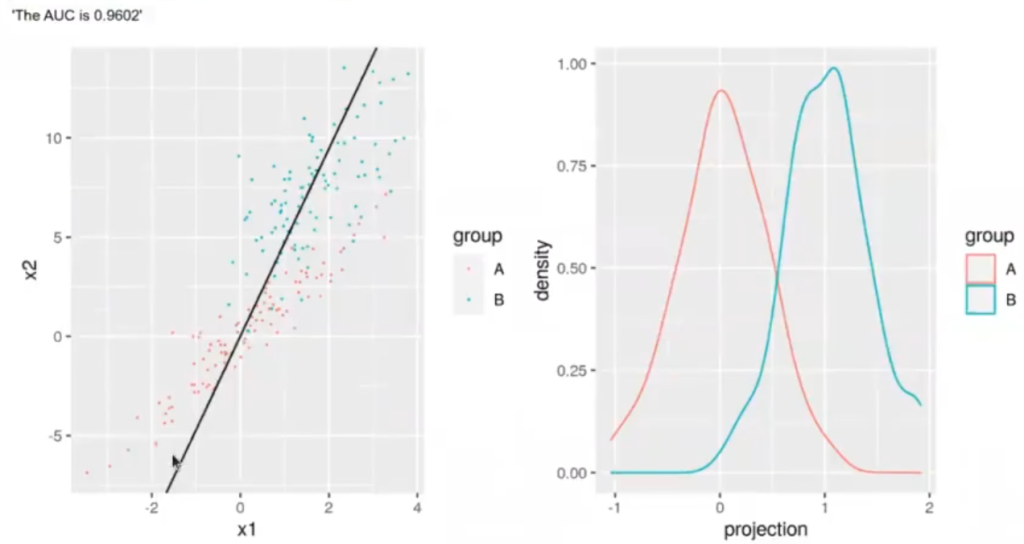
Lo que tratábamos de hacer en el ejercicio anterior era conseguir una línea recta que separara dos grupos de datos. Esta línea se ve representada en color negro en la imagen del lado izquierdo que verás un poco más abajo.
Ahora, lo que estamos buscando es una línea de proyección que nos permita separar las curvas de densidad del lado derecho, de forma que ambos picos de cada una de las curvas estén lo más separados posible.
Es muy importante aclarar que este es un ejercicio de aprendizaje supervisado, por tanto, sabemos cuáles son los puntos azules y cuáles son los puntos rojos.
El hecho de que las curvas de densidad estén más separadas entre sí nos dará un AUC más alto separando las curvas de densidad.
Consideremos que tenemos dos clases y un vector sobre el que proyectaremos las dos clases, de forma que podamos resumir el valor de cada muestra en una sola dimensión.
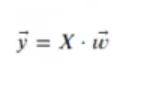
Donde:
- X son los datos que queremos clasificar: X E RNxp
- w es el vector de proyección: w E RPXL
- y son los datos proyectados: y E RNxI
Si sobre el valor de y definimos un umbral th0, de forma que si y >= th0 pertenece a una clase y si no a la otra, la elección del umbral y del vector w determinarán la calidad del carácter decisor.
Una posible idea sería seleccionar un vector w así:
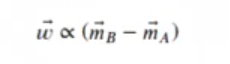
Donde:
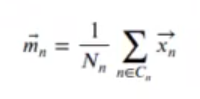
mA <- as.matrix (colMeans (subset (df, group == "A")[ , c ("x1", "x2")]))
mB <- as.matrix (colMeans (subset (df, group = "B")[ , c ("x1", "x2"))))
w <- mB - mA
w <- w / sum (w ^ 2)
w
x1 0.02896025
x2 0.13662008
#AUC más alto separando las curvas de densidad
gl <- ggplot (df, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.1) + geom_abline (slope = w [2] / w [1])
df$projection <- as.matrix (df [ , 2 : 3]) %*% w
g2 <- ggplot (df, aes (x = projection, color = group)) + geom_density ()
ggarrange (g1, g2, ncol = 2)
pr <- prediction (df$projection, df$group)
prf_auc = performance (pr, measure = "auc")
paste ("The AUC 15, [email protected] [[1]])
Aunque es una solución aparentemente buena no es el óptimo, Fisher lo que busca es el máximo del cociente:
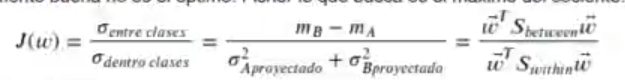
Donde Sbetween es la varianza que hay entre clases:
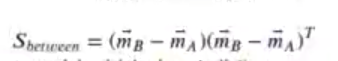
Recordemos la fórmula de la covarianza entre dos grupos x e y del módulo de estadística:
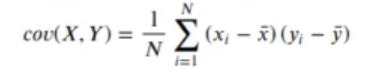
Donde Swithin es la suma de las varianzas de cada grupo:
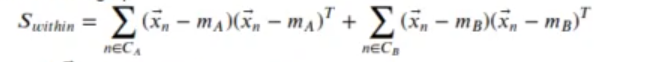
El mínimo de la función j(w) aparece para un w proporcional a:
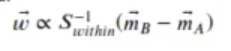
#AUC más alto separando las curvas de densidad
mA <- as.matrix (colMeans (subset (df, group == "A")[ , c ("x1", "x2")]))
mB <- as.matrix (colMeans (subset (df, group == "B")[ , c ("x1", "x2")]))
xA <- t (as.matrix (subset (df, group == "A") [ , c ("x1", "x2")]))
xB <- t (as.matrix (subset (df, group == "B") [ , c ("x1", "x2")]))
mA_rep <- matrix (rep (mA, each = ncol (xA)), ncol = ncol (xA), byrow = TRUE)
mB_rep <- matrix (rep (mB, each = ncol (xB)), ncol = ncol (xB), byrow = TRUE)
Sw <- (xA - mA_rep) % t (xA - mA_rep) + (xB - mB_rep) %*% t (xB = mB_rep)
w <- solve (Sw) %*% (mB - MA)
w <- w / sqrt (sum (w ^ 2))
w

#AUC más alto separando las curvas de densidad
gl <- ggplot (df, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.1) + geom_abline (slope = w [2] / w [1])
df$projection <- as.matrix (df [ , 2 : 3]) %*% w
g2 <- ggplot (df, aes (x = projection, color = group)) + geom_density ()
ggarrange (g1, g2, ncol = 2)
pr <- prediction (df$projection, df$group)
prf_auc = performance (pr, measure = "auc")
paste ("The AUC is", [email protected] [[1]])
The AUC is 0.9772′
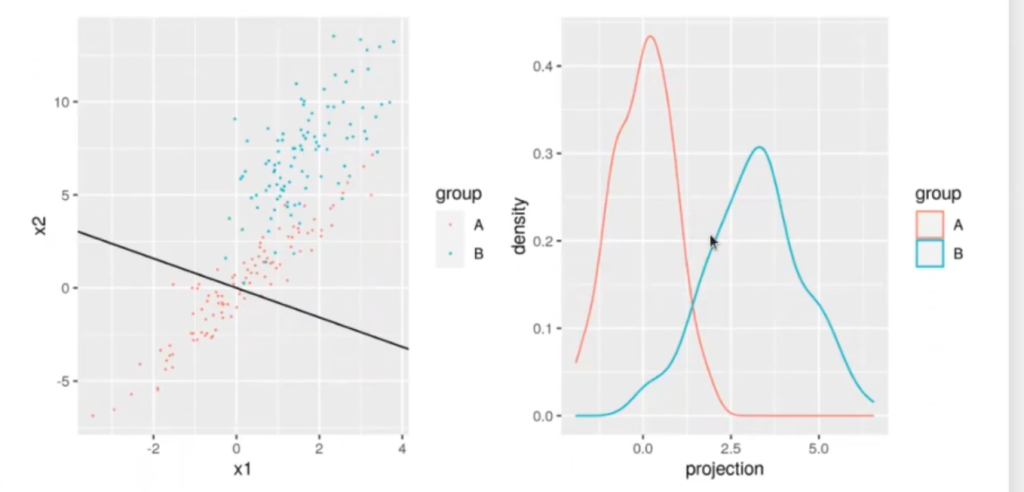
Con esto ya tenemos un clasificador y tenemos un AUC más alto separando las curvas de densidad.
¿Qué sigue?
Ahora que hemos aprendido cómo obtener un AUC más alto separando las curvas de densidad, podemos dar el siguiente paso para convertirte en un experto. Para conseguirlo tenemos nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos necesarios para incursionar en el mercado laboral en pocos meses. ¡Solicita más información!











