Probablemente ya sabrás que un sistema de ecuaciones lineales tiene la siguiente forma:
Ax B
Los autovalores y autovectores provienen de realizarse la siguiente pregunta: suponiendo que tenemos una matriz cuadrada A de n x n, ¿existe algún vector x distinto de 0 para el cual Ax es un escalar múltiplo de x? Si escribimos esta pregunta en lenguaje matemático, nos encontramos con la definición de los autovalores y autovectores:
Ax= λx
Cuando esta ecuación es válida y x no es 0, decimos que A es el Eigenvalue o autovalor de A, mientras x es su correspondiente Eigenvector o autovector.
Autovalores y autovectores: ejemplo
Veamos un ejemplo muy simple de autovalores y autovectores:
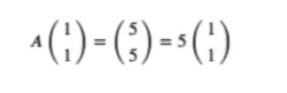
En este caso:
- λ = 5
- x = (1 / 1)
Vamos a intentar explicar con un ejemplo gráfico qué le sucede a los vectores cuando los multiplicamos por una matriz A. Consideremos que tenemos la siguiente matriz:
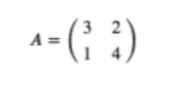
Si la multiplicamos por un vector:
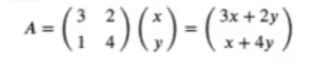
Para poder ver el efecto que hace dicha operación, vamos a considerar un cuadrado y vamos a resolver dicha ecuación para cada vértice del cuadrado por medio del patch Rectangle, es decir:
#Autovalores y autovectores
import matplotlib.pyplot as plt
plt.axes()
rectanble = plt.Rectangle ((0, 0), 1, 1)
plt.gca().add_patch (rectangle)
plt.xlim (-0.25, 1.25)
plt.ylim (-0.25, 1.25)
plt.grid()
plt.show()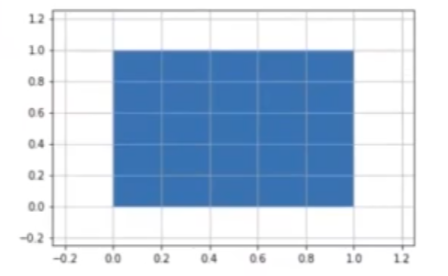
Los vértices del cuadrado son:
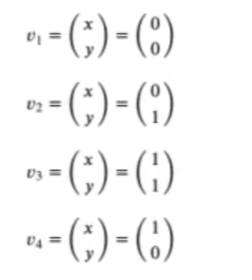
Si evaluamos la ecuación anterior en dichos puntos, obtenemos:
#Autovalores y autovectores
import numpy as np
A = np.array([[3, 2],
[1, 4]])
v1 = np.array([0, 0])
v2 = np.array([0, 1])
v3 = np.array([1, 1])
v4 = np.array([1, 0])#Autovalores y autovectores
A_v1 = np.dot(A, v1)
A_v2 = np.dot(A, v2)
A_v3 = np.dot(A, v3)
A_v4 = np.dot(A, v4)
print (A_v1)
print (A_v2)
print (A_v3)
print (A_v4)[0 0]
[2 4]
[5 5]
[3 1]
En resumen, hemos hecho estas operaciones:
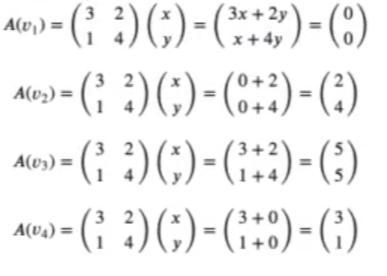
Podemos graficar esto:
#Autovalores y autovectores
from matplotlib.patches import Pölygon
pts = np.array([A_v1, A_v2, A_v3, A_v4])
p = Polygon (pts, closed = False)
ax = plt.gc ()
ax.add_patch(p)
ax.set_xlim(-0.25, 5.25)
ax.set_ylim(-0.25, 5.25)
ax.grid()
plt.show()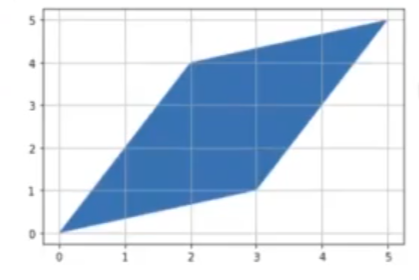
Uno de los componentes de los vectores (cuando pensamos en ellos geométricamente) es la dirección. ¿Se mantiene aquí la dirección de los vectores? Vamos a verlo:
- El punto v2 ha pasado de (0, 1) a (2, 4).
- El punto v4 ha pasado de (1.0) a (3.1).
- El punto v3 ha pasado de (1.1) a (5.5).
Vemos como el punto v3 es el único que ha mantenido su dirección; de hecho, se ha dilatado por 5. Este vector que ha mantenido su dirección se denomina autovector, y el factor de dilatación es el autovalor correspondiente.
Más arriba hemos visto la fórmula de los autovalores y los autovectores: Ax = λx. Podemos desarrollarla un poco:
Ax = λx
Moviendo un miembro al otro lado:
Ax – λx = 0
Multiplicando por I:
(A – λI) x = 0
El término (A – λI) se denomina matriz de coeficientes. Queremos obtener los resultados para cuando esta ecuación sea distinta a cero:
(A – λI) x = 0
Un escalar λ es un valor propio de la matriz A de (nxn), solo si λ satisface la ecuación característica:
det (A – λI) = 0
¿Quieres seguir aprendiendo?
Si quieres seguir aprendiendo, podrás acceder a una de las disciplinas más demandadas y con mejores sueldos de todo el mercado laboral en pocos meses con la guía del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos imprescindibles para obtener el trabajo de tus sueños. ¡Entra ya para solicitar información e impulsa tu carrera!



