En este artículo te enseñaremos cómo calcular el PCA con predict en R.
En un ejercicio anterior te hemos mostrado cómo calcular el PCA en R. Empezamos a trabajar con un dataset sobre la temperatura y el sol y normalizamos el pr_meteo, una matriz de rotación que también se puede normalizar con predict.
Eso es precisamente lo que haremos en este artículo; retomaremos este ejercicio y continuaremos para poder hacer el análisis de componentes y calcular el PCA con predict en R.
¿Cómo calcular el predict en R?
Lo primero que haremos será normalizar la matriz de rotación pr_meteo por medio del predict:
#Calcular el PCA con predict
head (predict (pr_meteo, as.matrix (df_meteo)))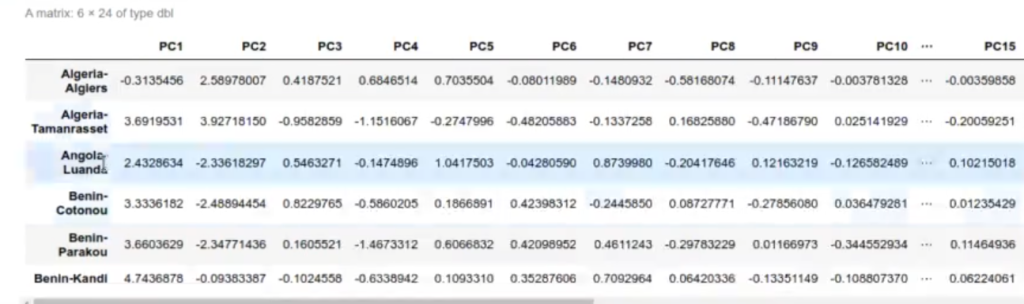
#Calcular el PCA con predict
str (pr_meteo)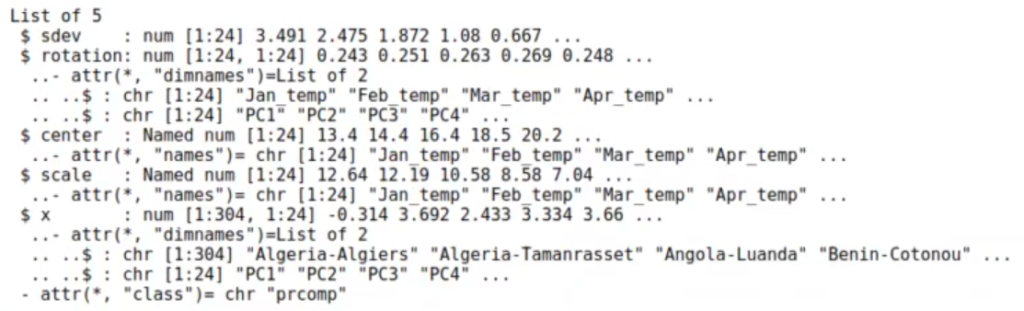
Aquí podemos observar la media y la desviación típica. En el $ center está la media y en el $ scale está la desviación típica.
Si pintamos estos valores transformados, estamos condensando toda la información que tenemos acerca de la temperatura y el sol de 12 meses. Estamos condensando 48 dimensiones (el valor de la matriz que teníamos inicialmente) en apenas 2:
#Calcular el PCA con predict
plot (pr_meteo$x [ , c (1, 2)])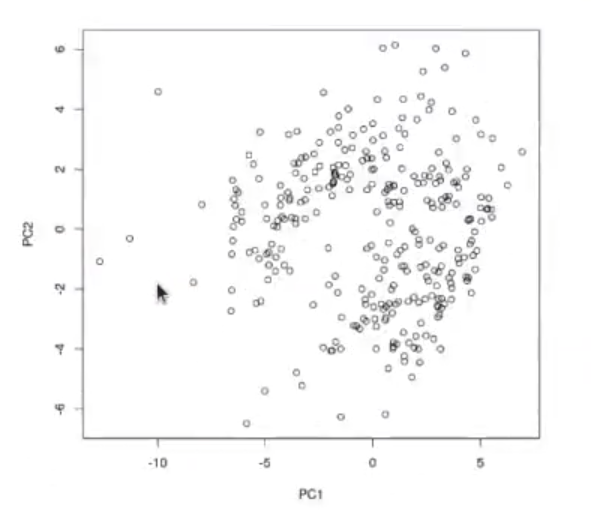
El siguiente paso es pintar ciertas ciudades, para que observemos cómo se comporta la matriz de datos:
#Calcular el PCA con predict
plot (pr_meteo$x [ , c (1, 2)])
city <- 'Spain - Barcelona'
points (pr_meteo$x [rownames (pr_meteo$x) == city, 1],
pr_meteo$x [rownames (pr_meteo$x) == city, 2],
col = 'red', pch ' * ' , cex = 3)
city <- 'Spain - Madrid'
points (pr_meteo$x [rownames (pr_meteo$x) == city, 1],
pr_meteo$x [rownames (pr_meteo$x) == city, 2],
col = 'blue', pch ' * ' , cex = 3)
city <- 'United ArabEmirates - Dubai'
points (pr_meteo$x [rownames (pr_meteo$x) == city, 1],
pr_meteo$x [rownames (pr_meteo$x) == city, 2],
col = 'green', pch ' * ' , cex = 3)
city <- 'Germany - Berlin'
points (pr_meteo$x [rownames (pr_meteo$x) == city, 1],
pr_meteo$x [rownames (pr_meteo$x) == city, 2],
col = 'brown', pch ' * ' , cex = 3)
city <- 'Colombia - Bogotá'
points (pr_meteo$x [rownames (pr_meteo$x) == city, 1],
pr_meteo$x [rownames (pr_meteo$x) == city, 2],
col = 'brown', pch ' * ' , cex = 3)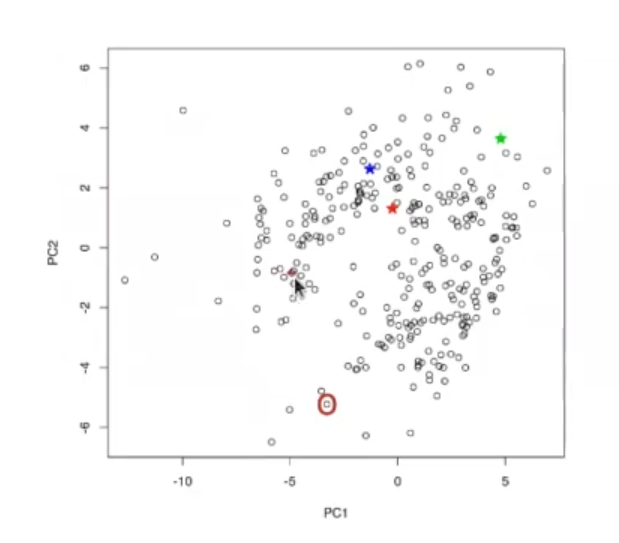
Observamos, pues, que la estrella verde corresponde a los Emiratos Árabes, el azul le pertenece a Madrid, el rojo a Barcelona y el marrón corresponde a Berlín y Bogotá.
Añadiremos la explicación de la matriz de rotación:
#Calcular el PCA con predict
pr_meteo$rotation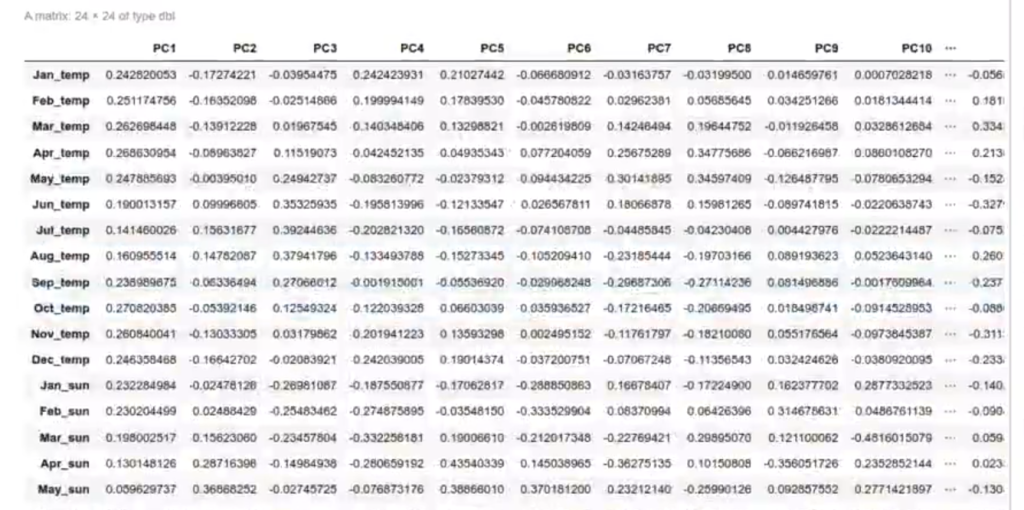
Para entender un poco mejor cómo funciona esto, tenemos la librería FactorMineR, a la que le pasaremos el dataframe. Viene por defecto en R.
#Calcular el PCA con predict
library ("FactorMineR")
#el res nos da el resultado del pca
res.pca <- PCA (df_meteo)
#Si hacemos un $eig nos da los autovalores y el porcentaje de la varianza
head (res.pca$eig)| eigenvalue | percentage of variance | cumulative percentage of variance | |
| comp 1 | 12.1855734 | 50.773223 | 50.77322 |
| comp 2 | 6.1266932 | 25.527889 | 76.30111 |
| comp 3 | 3.5048349 | 14.603479 | 90.90459 |
| comp 4 | 1.1656432 | 4.856847 | 95.76144 |
| comp 5 | 0.4452184 | 1.855077 | 97.61651 |
| comp 6 | 0.1856726 | 0.773636 | 98.39015 |
El primer autovalor nos da el 50% de la varianza, tal y como se muestra en la tabla. El siguiente nos da 25% y, entre los dos, tenemos alrededor de 75%, como podemos observar en la columna 3 de cumulative percentage of variance.
Este tipo de cálculos se usa mucho. De este modo determinamos cuántos componentes necesitamos para tener un porcentaje alto de varianza y qué componentes podemos desechar sin temor a error.
#Calcular el PCA con predict
plot (res.pca$eig [ , "eigenvalue"])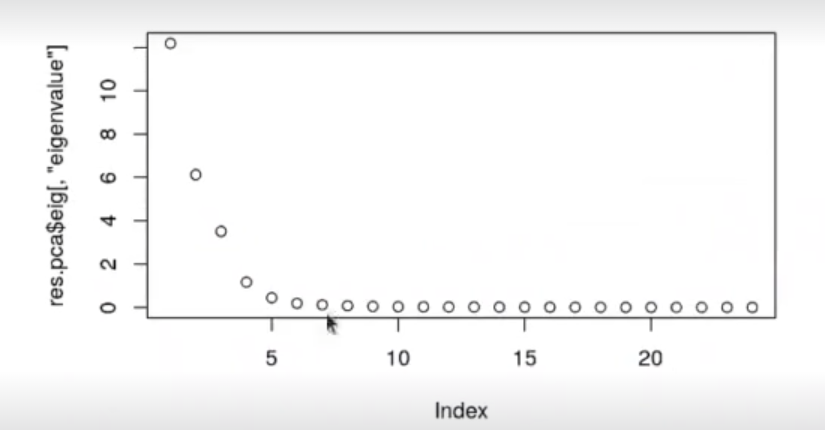
Aquí pintaremos el PCA y automáticamente el algoritmo nos coge las dos dimensiones principales, la del 50% y la del 25%.
plot (res.pca, choix = "ind", autoLab = "yes")Warning message:
«ggrepel: 290 unlabeled data points (too many overlaps). Consider increasing max.overlaps»
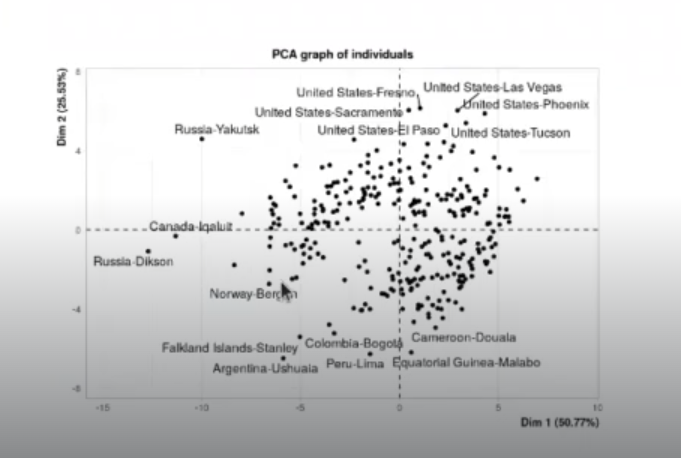
Aunque parezca que hay correlación, aún no debería haberla entre ninguna de las dos.
A continuación, tenemos la información de cómo van los autovectores en las dos dimensiones principales. Vemos cómo se representan cada una de las dimensiones originales de nuestra matriz.
plot (res.pca, choix = "var", autoLab = "yes")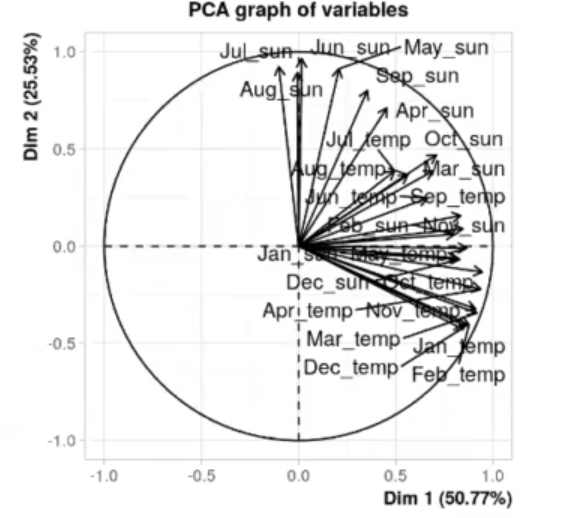
#Calcular el PCA con predict
pr_meteo$rotation [rownames (pr_meteo$rotation)
%in% c ('Jun_sun' , 'Jun_sun' , 'May_temp' , 'Oct_temp' ), 1 : 5]| PC1 | PC2 | PC3 | PC4 | PC5 | |
| May_temp | 0.247885693 | -0.00395010 | 0.24942737 | -0.08326077 | -0.02379312 |
| Oct_temp | 0.270820385 | -0.05392146 | 0.12549324 | 0.12203933 | 0.06603039 |
| Jun_sun | 0.004585101 | 0.38967807 | 0.02680110 | 0.09740561 | 0.17924080 |
| Jul_sun | -0.026135740 | 0.37319889 | 0.02867367 | 0.27506669 | 0.04415177 |
En este poste hemos visto cómo calcular el PCA con predict en R, un asunto importante cuando se trabaja con matrices y con datasets para el análisis. Si quieres seguir aprendiendo acerca de estas temáticas y otras tantas, te invitamos a seguir nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que en poco tiempo aprenderás todo lo necesario para incursionar en el mercado laboral. ¡Súmate a nuestro equipo y solicita más información!











