Calcular gradiente y matriz hessiana en R

La matriz hessiana es la generalización del concepto derivada segunda aplicada a funciones de vectores. En este artículo, te enseñaremos cómo puedes calcularla desde el lenguaje R y crear nuestra propia calculadora de matriz hessiana y la calculadora de gradientes.

Calcular matriz hessiana

Cuando hablamos de derivada primera en cálculo lineal y álgebra, hacemos alusión al gradiente. Cuando hablamos de derivada segunda, es lo que se conoce como matriz hessiana. Por eso, haremos nuestra calculadora de matriz hessiana.

Veamos:

Esto se convierte en una matriz de la siguiente forma:

La matriz Hessiana es el Jacobiano del gradiente.

Por ejemplo, sabemos que:

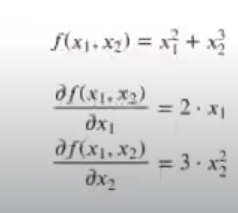
Su matriz hessiana se calcula así:

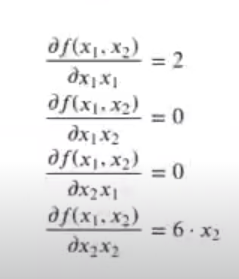
El resultado de la matriz hessiana es:

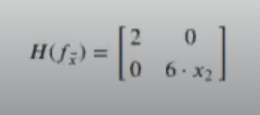
Aplicando esta fórmula, que no es más que el gradiente dividido, obtenemos otro método para calcular el mínimo de una función.

Ejemplo en R

En R podemos usar el paquete pracma, que tiene las funciones grad() y hessian() para calcular el gradiente y la matriz hessiana. Por ejemplo, vamos a calcular en R el gradiente y la matriz hessiana de f(x₁.x₂), en el punto [2,1], que sabemos que es:

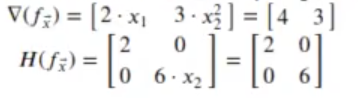
In [92]: library (pracma)
f_x1x2<-function (x) {x[1]^2+x[2]^3}
xvec <-c (2,1)
print ("El gradiente es:")
grad (f_x1x2, xvec)
print ("La matriz Hessiana es:")
hessian (f_x1x2, xvec)

[1] “El gradiente es:”
4.00000000002088
3.00000000007066

[1] “La matriz Hessiana es:”

In [ ]: library (pracma)
library (plotrix)
#my func30 <- function (x1,x2) (0.2*x1^4+x2^2}
myfunc3D <- function (x1,x2) (x1^2+3*x2^2}

myfuncVector <- function (x) { myfunc3D (x[1],x[2]) }

mygradient <- function (x, h, func){
      c((func (c (x [1] +h, x[2])) - func (x))/h,
          (func(c(x[1],x[2]+h))-func(x))/h) }

x_0 <- (-9, -9)
delta <- 0.025
delta <- 1

h < 0.001
criterio convergencia <- 0.05

x_historico <- data.frame (x=x_0 [1],y = x_0 [2])
for (i in 1:100) {
   #g <- mygradient (x_0, h, my funcVector)
     g <- inv (hessian (myfuncVector, x_0)) %*% as.matrix (grad      
       (myfuncVector, x_0), cols=1)
     x_new <- x_0 - g*delta
     if (abs(sum(g))<criterio_convergencia){
         break;
     }
     x_0 <- x new
     x_historico <- rbind (x_historico, data.frame (x = x_0 [1], y = x_0 [2])]
}
nrow (x_historico)

x1 <- seq (-10, 10, length-100)
x2 <- seq (-10, 10, length-100)
z <- oute r(x1,x2, my func3D)
image (x1,x2.z.col = terrain.colors (39))
contour (x1,x2,z, add = T)
points (x_historico$x, x_historico$y, col="black")
color scale.lines (x_historico$x,x historico$y, c(1,1,0)0, c(0,1,1), colvar=1:nrou(x_historico), lwd=3)

Problemas del método de Newton

A contninuación listamos algunos problemas para calcular la matriz hessiana.

• Calcular la matriz hessiana es costoso, computacionalmente hablando.
• Cuando la función es convexa y cuadrática, converge en un solo salto; si no es cuadrática, hacen falta más iteraciones.
• Es útil solo cuando el punto crítico cercano es un mínimo.

In [ ]: library(pracma)
library(plotrix)
myfunc30<-function (x1,x2) {sin(x1)*sin(x2)/(x1*x2)}
x <- seq(-10,10, length=100)
y <- seq(-10,10,length=100)
z <- outer(x,y,myfunc3D)
image (x,y,z,col = terrain.colors(39))
contour(x,y,z,add=T)

myfuncVector<- function(x) { myfunc30(x[1],[2]) }

x_0<- c(-2,-7)
#x 0 <- c(-5, 1)
#x 6 <- c(-5,-4)
x0<- c(0.7,2)
delta <- 0,1
criterio convergencia<-1e-1

x_historico<- data.frame(x=x_0[1],y=x_0[2])
for (i in 1:1000) {
       g <- grad(myfuncVector,x_0)
       g <- inv(hessian (myfuncVector,x_0)) %*% as.matrix(grad   
       (myfuncVector,x_0), cols=1)
       if (abs (sum(g)) <criterio_convergencia){
             break;
       }
       x_new <- x0 - g*delta
       x_historico<- rbind(x_historico,data.frame(x=x_0[1],y=x_0[2]))
}

paste("Numero pasos", nrow(x_historico))
paste("Valor alcanzado", myfuncVector(x_0))
points (x_historico$x,x_historico$y,col="black")
color.scale.lines (x_historicosx,x_historico$y, c(1,1,0),0,c(0,1,1),colvar=1:nrow(x_historico), lwd=3)

“Numero casos 34”

“Valor alcanzado 9.54876170723182e-05”

Recuerda que todas estas temáticas abordadas, sobre la calculadora de matriz hessiana, forman parte de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, donde podrás aprender todo lo relacionado con el mundo del Big Data e incursionar en poco tiempo en un amplio y prolífico mercado laboral. ¡Te esperamos!