La energía neta es la diferencia entre la energía producida por una instalación o tecnología energética y la energía requerida para desarrollarla y operarla. La energía requerida incluye la energía para producir todos los insumos, como acero, hormigón, etc. En este post, te explicamos cómo calcular producción de energía neta con R.
Calcular producción de energía neta con R
E este ejemplo sobre cómo calcular producción de energía neta con R, vamos a predecir la potencia de generación de energía neta de una central de ciclo combinado.
El conjunto de datos contiene 9568 puntos de datos recopilados de una Central de Ciclo Combinado durante 6 años (2006-2011), cuando la planta de energía se puso a funcionar con carga completa. Las características consisten en variables ambientales promedio por hora [temperatura ambiente (AT), presión ambiente (AP), humedad relativa (HR) y vacío de escape (V)] para predecir la producción de energía neta eléctrica por hora (PE) de la planta.
Las características consisten en variables ambientales promedio por hora:
- Producción de energía neta eléctrica por hora (PE) 420 26-495,76 MW.
- Temperatura (AT) en el rango de 1.81 Cy 37.11 C.
- Presión ambiental (AP) en el rango de 992.89-1033.30 milibares.
- Humedad relativa (HR) en el rango de 25.56% a 100.16%.
- Vacío de escape (V) en el rango de 25,36-81.56 cm Hg.
Los promedios se toman de varios sensores ubicados alrededor de la planta que registran las variables ambientales cada segundo. Las variables se dan sin normalización.
In [55]: powerplant-read.csv ("data/powerplant.csv)
options (repr.plot.height = 4, repr.plot.width = 5)
plot (powerplant, pch = ' . ')
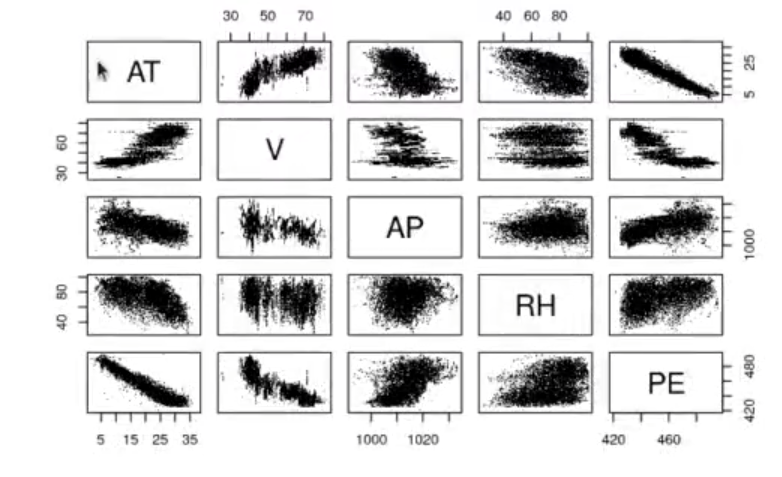
In [ ]: Library(GGally)
ggpairs (powerplant, lower_list (continuous = wrap("density", alpha = 0.8,size 0.2, color = "blue"))
#lower = list(continuous = wrap ("points", alpha-0.3, size-01, color-'blue'))Registered 53 method overwritten by ‘GGally’:
method from
+.99 ggplot2
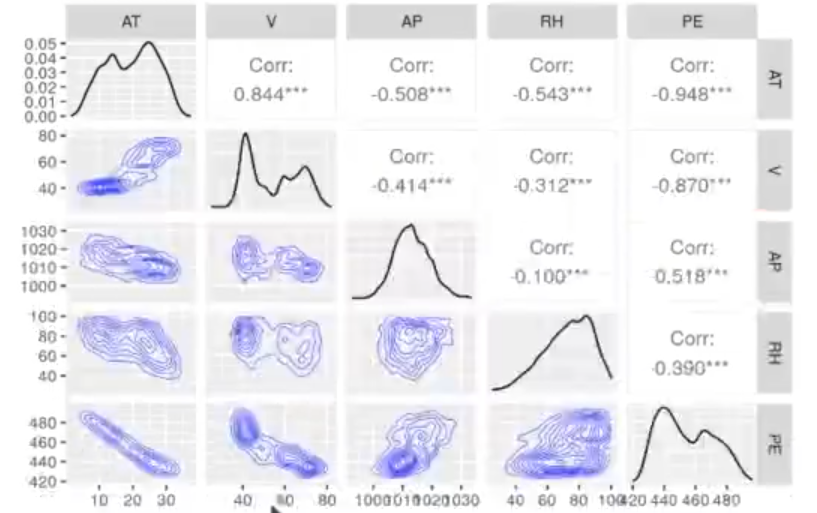
In [ ]: set.seed(12345)
idx <- sample (l:nrow (powerplant), nrow (powerplant) * 0.7)
idx
powerplant.train <- powerplant [idx,]
powerplant.test <- powerplant [-idx,]
model_powerplant <- lm (PE-., data = powerplant.train)
summary (model_powerplant)
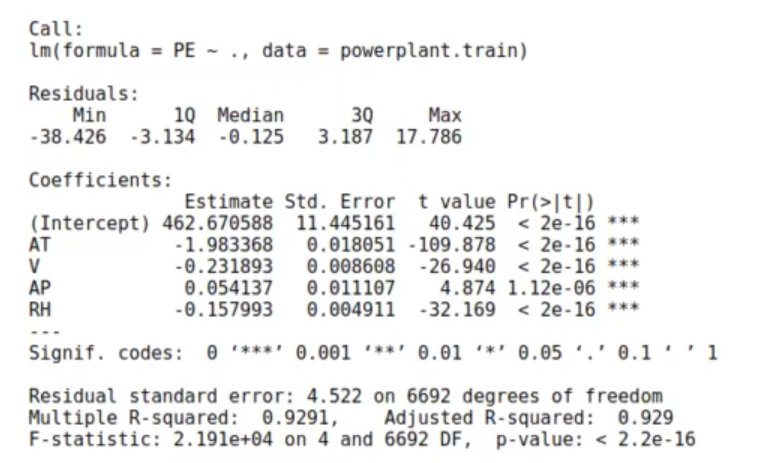
powerplant.test <-powerplant [-idx,]
In [ ]: powerplant.train$pe est <- predict (model powerplant, powerplant.train)
#plot (powerplant.train$PE, (powerplant.train$PE-powerplant.train$pe_est) ^2)
plot(powerplant.train$PE, (powerplant.trainsPE - powerplant.trainspe est))
paste ("MSE:", sqrt (mean((powerplant.train$PE - powerplant.trainspe_est)^2)))
paste("R^2:", myrsquared (powerplant.train$PE, powerplant.trainspe est))
caret :: postResample (pred = powerplant.train$pe_est, obs = powerplant.train$PE)‘MSE_ 4.52060572398258’
‘R ^2: 0.92906168865458’
RMSE: 4.52030572398258
Rsquared: 0.92906168865458
MAE: 3.6081817956587
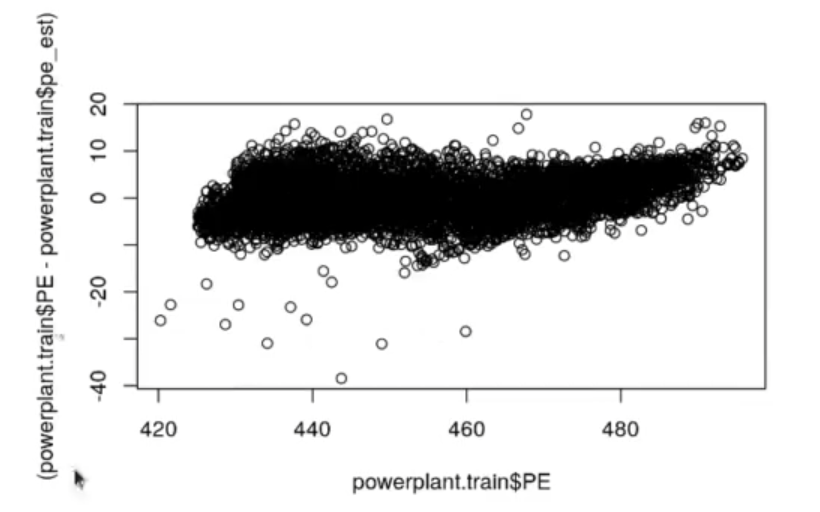
Siguiendo con el ejemplo de producción de energía neta, en la gráfica anterior observamos que la varianza de los residuos es más o menos constante a lo largo de todo el rango predicho. Es decir, no hay heterocedasticida o hay muy poca en el proceso de producción de energía neta.
En la siguiente podemos ver como los residuos siguen una distribución normal:
In [67]: hist (powerplant.train$PE - powerplant.train$pe_est, 20)
qqnorm (powerplant.train$PE - powerplant.train$pe_est)
qqline (powerplant.train$PE - powerplant.trainspe_est, col = 'orange', lwd = 2)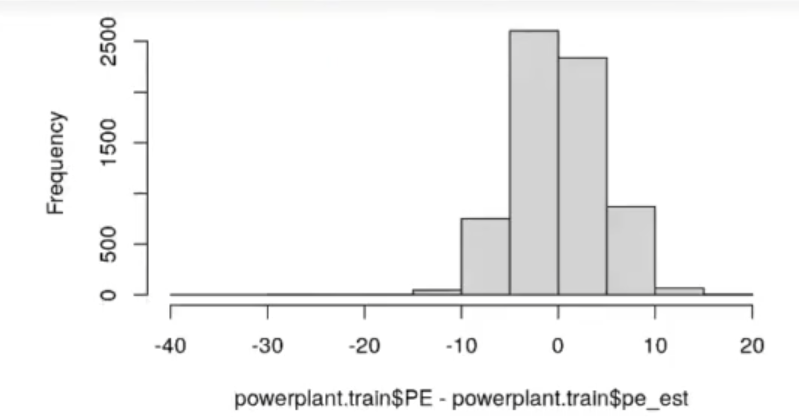
Ahora vamos a pintar los resultados:
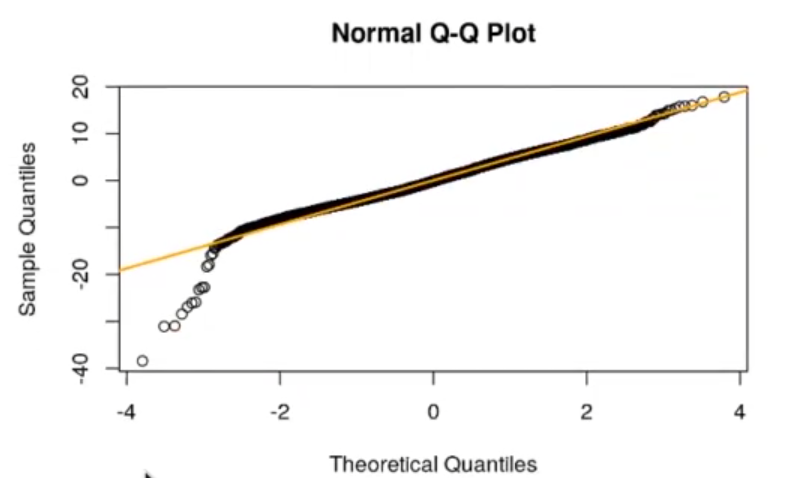
Si realizamos un test de Shapiro, son los mismos residuals que el valor real menos el predicho en los cálculos de producción de energía neta:
In [69]: shapiro.test (model_powerplant$residuals [sample (l:nrow (powerplant.train), 1800)])Shapiro-Wilk normality test
data: model_powerplant$residuals (sample (l:nrow (powerplant.train), 1000)]
W = 0.98035, p-value = 2.285e-10
In [ ]: ks.test ( (powerplant.train$PE - powerplant.train$pe_est), pnorm, 0, sd((powerplant.train$PE-powerplant.train$pe_est) ) )
Analicemos ahora el conjunto de test:
In [ ] : powerplant.test$pe_est <- predict (model_powerplant.powerplant.test)
plot (powerplant.test$PE, (powerplant.test$PE - powerplant.testspe_est) )
caret :: postResample (pred = powerplant.test$pe_est, obs = powerplant.test$PE)
hist(powerplant.test$PE - powerplant.test$pe_est, 20)
qqnorm (powerplant.test$PE - powerplant.test$pe_est)
qgline (powerplant.test$PE - powerplant.test$pe_est, col = 'orange', lwd = 2)Concluimos que, en general, todos los test tienen distribuciones gaussianas y que son resultados estables.
Ahora que ya sabes calcular producción de energía neta con R, recuerda que toda la temática abordada en este post puedes encontrarla en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Aquí podrás aprender lo necesario para incursionar en el mercado laboral de manera rápida. ¡Te esperamos!



