Ejemplo de cartera de fondo de inversión en R

En este artículo te mostraremos un ejemplo de cartera de fondo de inversión en R para minimizar la varianza.

Cartera de fondo de inversión en R

Partimos de varios fondos de inversión y queremos una cartera que nos maximice el retorno medio en un año mientras minimiza la varianza. Para ello, buscamos calcular unos coeficientes que nos digan qué porcentaje de nuestra cartera corresponde a cada fondo de inversión en R.

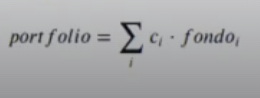
Cargamos la cartera de fondo de inversión en R con la rentabilidad a un año vista:

In [132]: funds <- read.csv ('data/fondos_inversion.csv')
funds$date <- as.Date(funds$date)

In [133]: head (funds)

	date	fondo.1	fondo.2	fondo.3	fondo.4	fondo.5	fondo.6	fondo.7	fondo.8	fondo.9	fondo.22	fondo.23	fondo.24	fondo.25
	<date>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	2015-04-17	1.242626	1.450498	1.283821	1.283720	1.521607	1.521640	1.351085	1.242052	1.213878	1.440002	1.342162	1.828762	1.348290
2	2015-04-18	1.242626	1.450498	1.283821	1.283720	1.521607	1.521640	1.351085	1.242052	1.213878	1.213878	1.342162	1.828762	1.348290
3	2015-04-19	1.242626	1.450498	1.283821	1.283720	1.521607	1.521640	1.351085	1.242052	1.213878	1.213878	1.342162	1.828762	1.348290
4	2015-04-20	1.253286	1.466606	1.265939	1.268815	1.516662	1.516696	1.351525	1.252615	1.226382	1.455206	1.326655	1.782250	1.339593
5	2015-04-21	1.259490	1.457408	1.278023	1.278035	1.536047	1.536077	1.347879	1.258899	1.231648	1.454298	1.339061	1.829459	1.348979
6	2015-04-22	1.242891	1.460447	1.269861	1.269787	1.557659	1.557659	1.344193	1.242287	1.212525	1.448107	1.335252	1.861152	1.357175

Esto lo podemos pintar así:

In [135]: library (ggplot2)
ggplot (funds, aes(x = date)) + geom_line (aes (y = fondo.1.color = "fondo1")) + geom_line (aes (y = fondo.2, color = "fondo2"))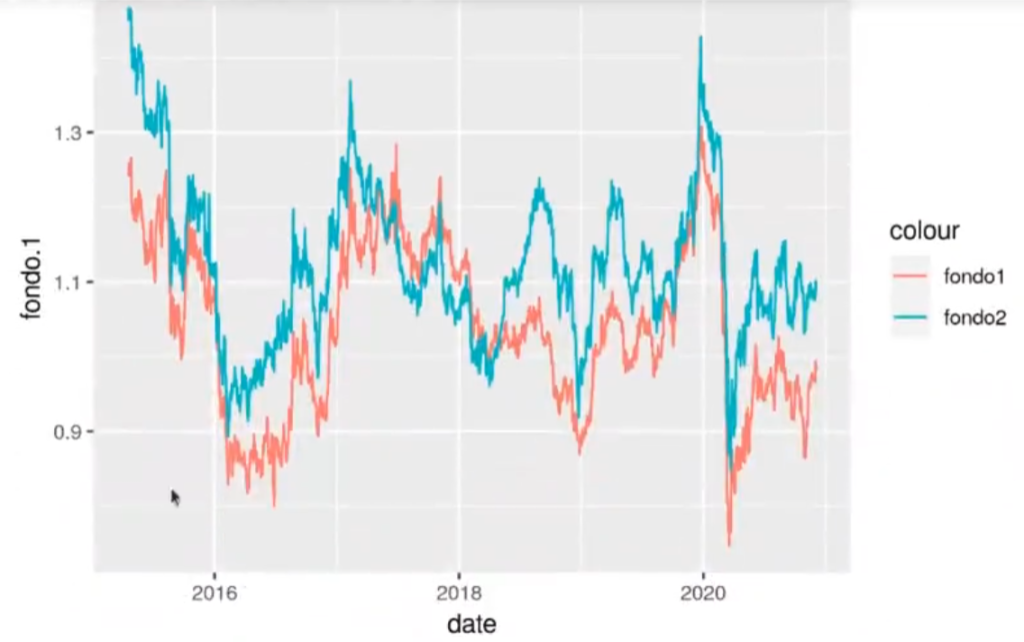

In [136] : df_subset <- funds
df_subset$date <- NULL

Queremos optimizar un retorno máximo y una varianza mínima de nuestro portafolio:

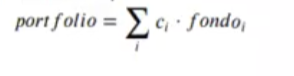
Dadas las variables:

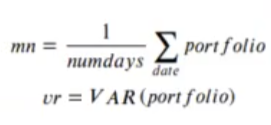
Queremos encontrar los coeficientes c₁, de forma que la siguiente función sea mínima:

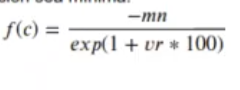
Debe cumplir las siguientes limitaciones:

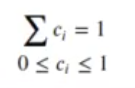
In [137]: library(pracma)
variance_importance <- 100

roi_optim <- function (coefs) {
mn <- mean (rowSums (repmat (coefs, nrow(df_subset),1) * df_subset))
vr <- var (rowSums (repmat (coefs, nrow(df_subset), 1) * df_subset)) 
return (-mn/exp (1 + variance_importance * vr))
#return (mn)
}
constrain_func <- function (coefs) {
sum(coefs)
}
In 11: x0 <- rep(1/ncol (df_subset), ncol (df_subset)) #Valor inicial de los coeficientes
lx <- rep (0, lenght (x0)) #Valor mínimo de los coeficientes
ux <- rep (1, lenght (x0)) #Valor máximo de los coeficientes
soll <- Rsolnp :: solnp (x0, fun = roi_optim, eqfun = constrain_func, eqB = 1, LB = lx, UB = ux)

In [139] : lx

0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0- 0-

In [140]: ux

1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1- 1-

In [141] : soll$pars

8.51600458131105e-08 – 2.37396166066272e-08 – 9.80498626556178e-09 – 9.79624168211611e-09 – 7.55872530855147e-08 – 3.81844795504704e-05 – 0.115153571187694 – 2.37490219608833e-08 – 3.36953190604144e-08 – 2.84152953887565e-08 – 8.55404748007717e-08 – 2.99134401863966e-08 – 3.60547670800086e-08 1.76651394740702e-08 – 2.42111850443934e-08 – 2.8458842850002e-08 – 3.00636014668393e-08 – 0.357986118890563 – 0.329013969300045 – 3.4446595251685e-08 – 3.44991721343077e-08 – 7.15215851504688e-08 – 2.6623767557937e-08 – 1.10224127479035e-06 – 2.45417759315134e-08 – 1.9613507034608e-11 – 0.197804682962264 – 155764146919459e-06 – 3.54567273528448e-08 – 3.53159129983526e-08 – 9.01675885049376e-09

In [ ]: coefs <- soll$pars
names (coefs) <- colnames (df_subset)
coefs <- round (coefs [coefs > 1e - 2], 4)
coefs <- coefs/sum (coefs)

In [ ] : coefs

Para calcular el fondo de inversión en R agregado resultante sería:

In [142]: coefs <- soll$pars
names (coefs) <- colnames (df_subset)
coefs <- round (coefs [coefs > le-2], 4)
coefs <- coefs/sum (coefs)

In [143]: coefs

fondo.10: 0 1152

fondo.15: 0.329

fondo.19: 0.358

fondo.20: 0.1978

In [144] : funds ["portfolio"] <- as.matrix (funds [names (coefs) ] ) %*% coefs

In [145] : head (funds)

In [146] : ggplot (funds, aes(x=date)) + geom_line (aes (y = portfolio, color = "minima varianza")) +
geom_line (aes (y = fondo.10, color = "fondo 10"))+
geom Line (aes (y-fondo.15.color="fondo.15"))+
geom_line (aes (y = fondo.19, color = "fondo, 19))+
geom line (aesty-fondo.28.color" fondo.20"))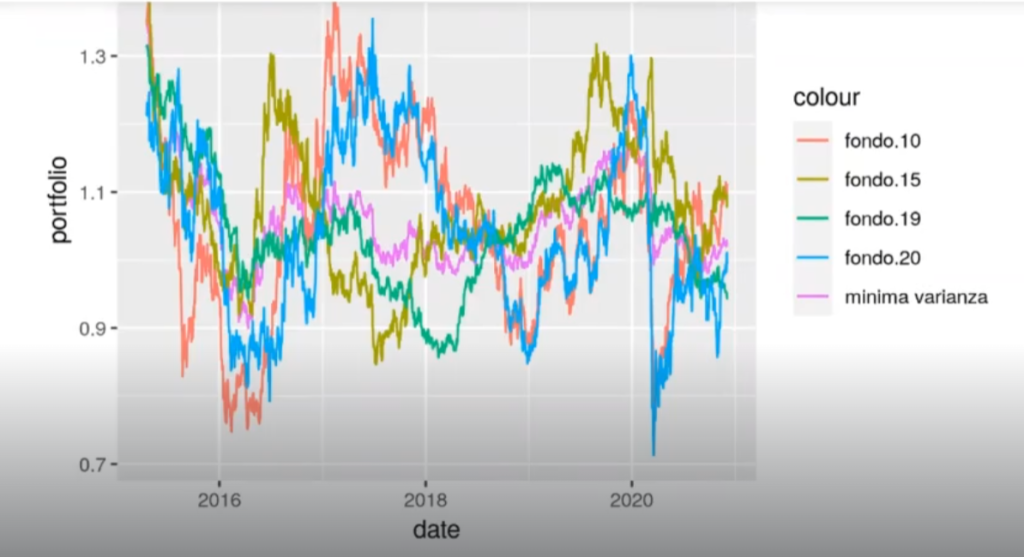

In [147]: 10 ^ (colMeans (log10 (funds [c ("portfolio", names (coefs)) ] ) ))

portfolio: 1.0577233152499

fondo.10: 1.04435252394117

fondo.15: 1.07308781575452

fondo. 19: 1.04087504856109

fondo.20: 1.03798441709755

In 1: apply (funds [c ("portfolio", names (coefs))], 2, var)

portfolio: 0.00439885329302952

fondo.10: 0.0192770515898909

fondo.15: 0.0106828702655021

fondo. 19: 0.00767870804654685

fondo.20: 0.015899536378032

En este artículo hemos visto un ejemplo de cartera de fondo de inversión en R para minimizar la varianza. Para ello, juntamos varios fondos de inversión. Lo que buscamos con ellos es una cartera que nos maximice el retorno medio a un año mientras minimiza la varianza del mismo.

Hemos calculado los coeficientes que nos muestran el porcentaje de nuestra cartera que corresponde a cada fondo de inversión en R.

Recuerda que este tema y muchos otros forman parte de nuestro Bootcamp en Big Data, una formación intensiva en la que podrás aprender, en tan solo 8 meses, todo lo necesario para incursionar en el prolífico mercado laboral del Big Data. ¡Anímate a preguntar para obtener más información, te esperamos!