En este artículo veremos un caso linealmente no separable de SVM.
Recordemos que SVM significa support vector machines y que estas fueron concebidas para solucionar, principalmente, problemas de clasificación, aunque también funcionan con problemas de regresión.
¿Por qué Support Vectors?
Se puede demostrar que la solución de las SVM es una combinación lineal de las muestras de entrenamiento.
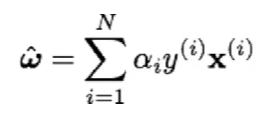
Tenemos que α1 >= 0, pero para muchas muestras se cumple que α1 = 0 (solución dispersa).
Entonces, los vectores soporte son las muestras para las que α1 ≠ 0.
¿Cuál es, pues, la interpretación física de los vectores soporte y por qué se llaman así?
Se puede demostrar que la solución es:
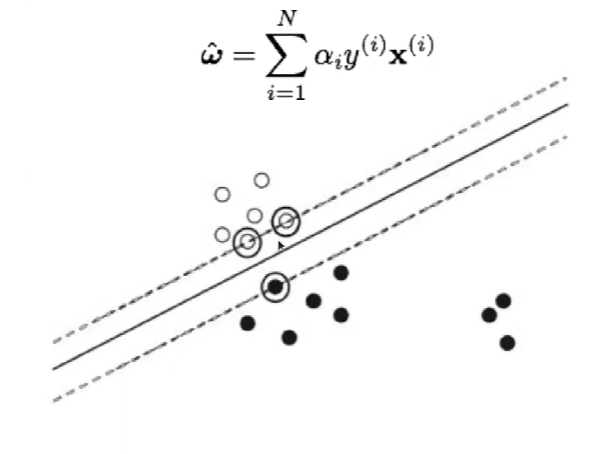
Frontera de separación
Conocidos los pesos, la predicción se realiza a través de la fórmula:
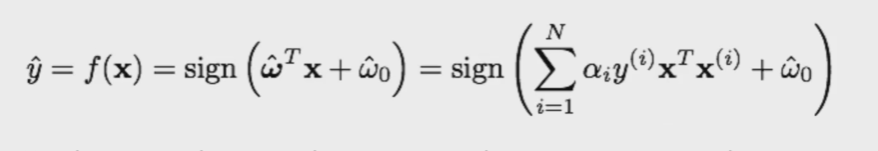
Producto escalar entre las muestras de entrenamiento y la muestra sobre la que queremos realizar la predicción.
Caso linealmente no separable de SVM
Hasta ahora hemos trabajado con un caso en el que las clases son claramente separables, esto es, no hay solapamiento entre ellas. No hablamos de fronteras no lineales, seguimos considerando que existe un hiperplano capaz de separar las clases, aunque con errores, se trata del caso linealmente no separable de SVM.
Vamos a permitir errores, es decir, muestras dentro del margen o mal clasificadas. Exclusivamente a esas muestras les asignamos un error (slack variable).
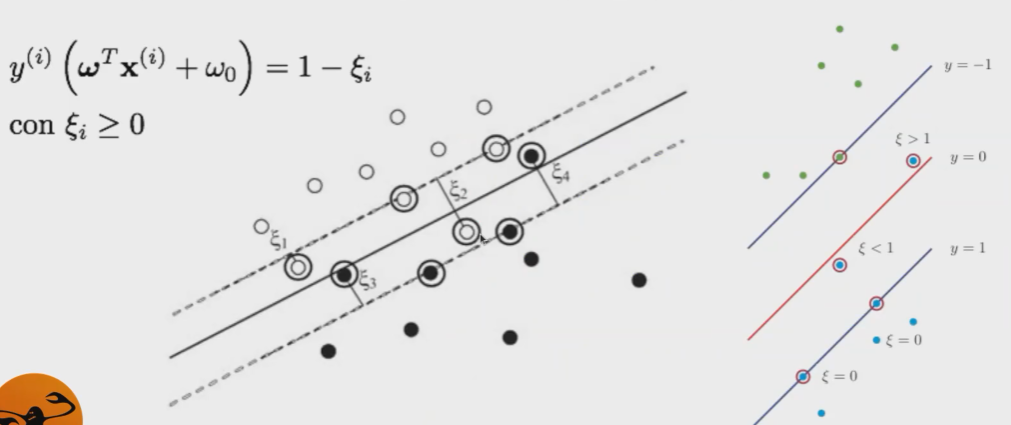
No obstante, penalizamos los errores con un coste C.
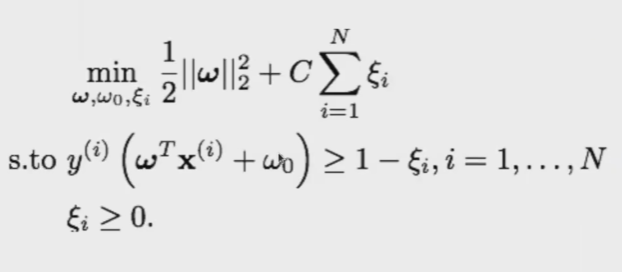
Parámetro de regularización C
- C: cota superior al número de errores.
- Compromiso entre margen y errores en la solución.
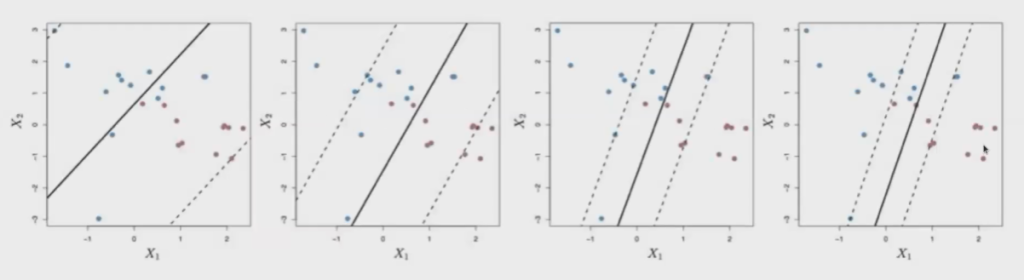
- Si C es elevado y el margen estrecho, se le dará más peso a los errores. Esto implica alta complejidad.
- Si C es pequeño y el margen estrecho, se le dará menos peso a los errores, lo cual implicará una baja complejidad.
La solución al caso linealmente no separable de SVM quedaría así:
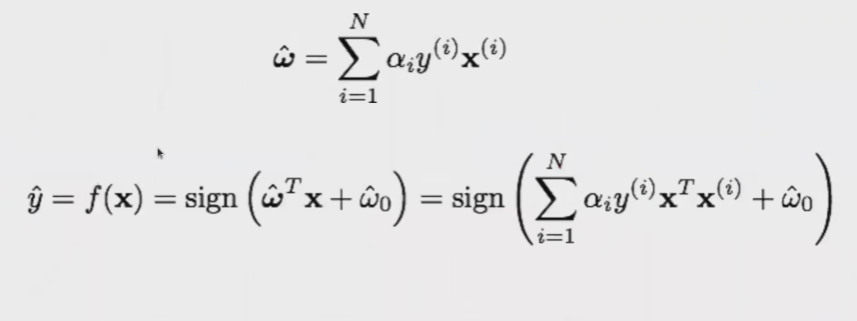
¿Quieres seguir aprendiendo sobre Big Data?
Si te ha interesado este tema sobre caso linealmente no separable de SVM y quieres seguir aprendiendo sobre Big Data, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación de alta intensidad en la que tendrás la oportunidad de adquirir todas las herramientas teóricas y prácticas para incursionar en un mercado laboral lleno de buenas oportunidades. ¡No esperes más para iniciar tu ascenso al éxito y solicita más información ahora!



