En este artículo, te enseñaremos cómo es el proceso de codificación de variables categóricas, un tipo de variables en el que se clasificana los individuos o casos.

Métodos de codificación de variables categóricas

One-hot

En este método de codificación de variables categóricas se crean N columnas nuevas, tantas como posibles valores tenga la variable categórica. Se asigna un valor de 1 a la variable que tiene ese valor 0 en caso contrario.

–	col1	col2	col3	col4
categoria1	1	0	0	0
categoria2	0	1	0	0
categoria3	0	0	1	0
categoria4	0	0	0	1

In [118]: df_new_econding <- df_weight_height
df_new_econding$boy <- ifelse (df_new_econding$gender == "boy", 1, 0).
df_new_econdingsgirl <- ifelse(df_new_econdingsgender == "girl", 1, 0)
df_new_econdingsgender <- NULL
#set.seed(123)
#idxe <- sample (1:nrow (df_new_econding), nrow (df_new_econding) * 0.7)
train.df <- df_new_econding [idx,]
test.df <- df_new_econding [-idx,]

In [ ] : head (train.df)

	day	height	weight	boy	girl
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
159	115	61.69181	7.033859	1	0
179	1355	102.24834	18.256696	0	1
14	818	88.38173	10.859407	0	1
195	741	85.26628	13.393031	1	0
170	1523	104.22974	14.486120	1	0
50	1163	95.89462	12.668591	1	0

In [120] : model <- lm (data = train.df, formula = height - day : boy + day : girl)
summary(model)

Call:

lm (formula = height – day:boy + day:girl, data = train.df)

Residuals:

Min: -10.429

1Q: -2.881

Median: 0.110

3Q: 3.566

Max: 10.293

Coefficients:

	Estimate	Std.	Error	t value	Pr (>ltl)
(Intercpet)	62.604255	0.	743537	84.20	<2e – 16 ***
	0.29221	0.	000852	34.30	<2e – 16 ***
	0.027593	0.	000808	34.15	<2e – 16 ***

---

Signif. codes:

0 ‘ *** ‘

0.001 ‘ ** ‘

0.01 ‘ * ‘

0.05 ‘ . ‘

0.1 ‘ ‘

1

Residual standard error: 4.632 on 137 degrees of freedom

Multiple R-squared: 0.9162,

Adjusted R-squared: 0.915

F-statistic: 748.9 on 2 and 137 DF, p-value: < 2.2e – 16

In [ ] : model<-lm(data-train.df, formula-height-day+girl) summary(model)

Call:

ln (formula = height – day + girl, data = train.df)

Residuals:

Min: .10.1152

1Q: -2.8007

Median: 0.0805

3Q: 3.5784

Max: 10.0219

Coefficients:

	Estimate	Std.	Error	t value	Pr (> ltl)
(Intercept)	63.2007484	0.	8666949	72.922	<2e – 16 ***
day	0.0283134	0.	0007393	38.296	<2e – 16 ***
girl	-1.0691758	0.	7942038	-1.346	0.18

---

Signif. codes:

0 ‘ *** ‘

0.001 ‘ ** ‘

0.01 ‘ * ‘

0.05 ‘ . ‘

0.1 ‘ ‘

1

Residual standard error: 4.675 on 137 degrees of freedom

Multiple R-squared: 0.9146

Adjusted R-squared: 0.9134

F-statistic: 733.9 on 2 and 137 DF, p-value: < 2.2e-16

Dummy

En la codificación de variables categóricas por el método Dummy, se crean N-1 columnas nuevas, tantas como posibles valores tenga la variable categórica menos una. Así, habrá una categoría en la que todos los valores serán 0 y esa categoría se usará como base del modelo.

En este método de codificación de variables categóricas, al resto de columnas se le asigna un valor de 1 a la variable que tiene ese valor 0 en caso contrario.

–	col1	col2	col3
categoria1	0	0	0
categoria2	1	0	0
categoria3	0	1	0
categoria4	0	0	1

In [122] : df_new_econding <- df_weight_height
df_new_econding$girl <- ifelse (df_new_econding$gender == "girl", 1, 0)
df_new_econdingsgender <- NULL
set.seed(123)
idx <- sample (l:nrow (df_new_econding), nrow(df_new_econding) * 0.7)
train.df <- df_new_econding [idx,]
test.df <- df_new_econding [-idx,]

In [123]: head (train.df)

	day	height	weight	girl
	<int>	<dbl>	<dbl>	<dbl>
159	115	61.69181	7.033859	0
179	1355	102.24834	18.256696	1
14	818	88.38173	10.859407	1
195	741	85.26628	13.393031	0
170	1523	104.22974	14.486120	0
50	1163	95.89462	12.668591	0

In [124] : model <- lm (data = train.df, formula = height - day + day : girl)
summary (model)

Call:

lm (formula = height – day + day : girl, data = train.df)

Residuals:

Min: -10.429

1Q: -2881

Median: 0.110

3Q: 3.566

Max: 10.293

Coefficients:

	Estimate	Std.	Error	t value	Pr (>ltl)
(Intercept)	62.604255	0.	743537	84.198	<2e – 16 ***
day	0.029221	0.	000852	34.299	<2e – 16 ***
day:girl	-0.001628	0.	000776	-2.097	0.0378 *

Signif. codes:

0 ‘ *** ‘

0.001 ‘ ** ‘

0.01 ‘ * ‘

0.05 ‘ . ‘

0.1 ‘ ‘

1

Residual standard error: 4.632 on 137 degrees of freedom
Multiple R-squared: 8.9162
Adjusted R-squared: 0.915
F-statistic: 748.9 on 2 and 137 DF, p-value: < 2.2e-16

In [125] : paste ("El coeficiente final para las niñas es:, modelscoefficients [2] + modelscoefficients [3] )

«El coeficiente final para las niñas es: 0.0275933503254364

La ecuación equivalente seria:

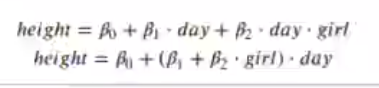
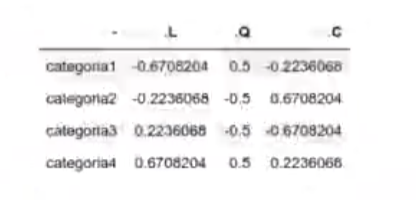
Ortogonal de polinomios

La codificación de variables categóricas por ortogonal de polinomios es una forma de análisis de tendencias, ya que busca tendencias lineales, cuadráticas, cúbicas, grado-n, etc. en la variable categórica.

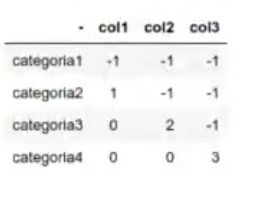
Codificación Helmert

La codificación de variables categóricas por el método Helmert compara cada nivel de una variable categórica con la media de los niveles subsiguientes.

¿Qué sigue ahora?

Existen otros métodos de codificación de variables categóricas, pero los dos primeros, el dummy y el one-hot, son los más importantes. Estos métodos son de gran relevancia en los análisis estadísticos y en el Big Data, por eso, te invitamos a que aprendas más sobre ellos con nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En muy poco tiempo, podrás formarte en todo lo necesario para incursionar en el mercado laboral. ¡Entra y apúntate!