¿Sabes qué son las combinaciones lineales entre vectores y cuál es su función en los conjuntos de vectores? En este post, te instruiremos acerca de uno de los temas básicos del álgebra.
¿Qué son las combinaciones lineales entre vectores?
Dados los vectores v1, v2, …, vj en V y los escalares c1, c2, …, cj en K, se denomina combinación lineal al vector y definido por:
y = c1 v1 + … + cj
Las combinaciones lineales entre vectores no son más que una expresión matemática construida sobre un conjunto de vectores, en el que cada vector es multiplicado por un escalar y los resultados, después, se suman. Matemáticamente, lo podemos expresar de la siguiente forma:
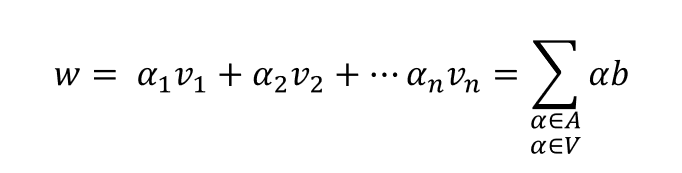
En una combinación lineal, los coeficientes pueden ser cualquier número real, incluso el cero.
Ejercicio sobre combinaciones lineales entre vectores
Dados los vectores v1 = (1, 2) y v2 = (1, -1), hallar el vector combinación lineal z = 2v1 + 3v2.
Lo primero que haremos será graficar los dos vectores que tenemos, tanto v1 como v2.
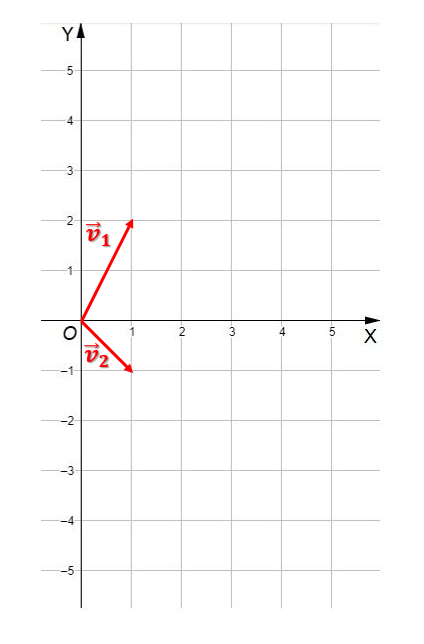
Lo que nos dice el ejercicio sobre combinaciones lineales entre vectores es que hallemos un vector que sea 2v1 + 3v2. Primero desglosaremos:
v1 = [1, 2] * 2 → [2, 4] = 2v1
v2 = [1, -1] * 3 → [3, -3] = 3v2
Ahora vamos a volver a graficar los nuevos vectores:
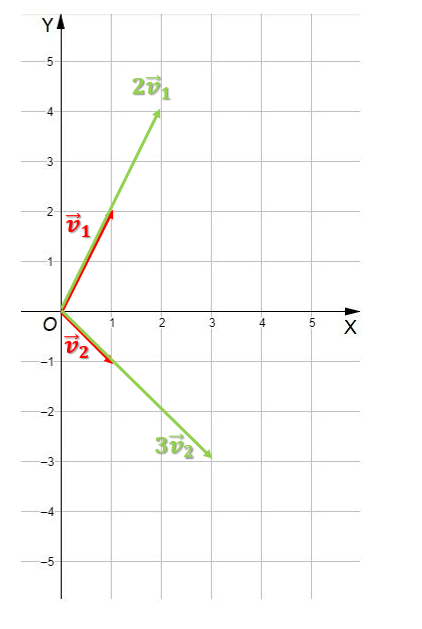
Este era el primer paso del ejercicio sobre combinaciones lineales entre vectores. Ahora bien, el segundo paso está dado por la suma de los vectores:
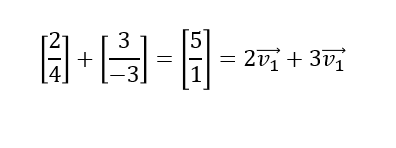
Ahora, dibujaremos el vector entero de 2v1 + 3v2:
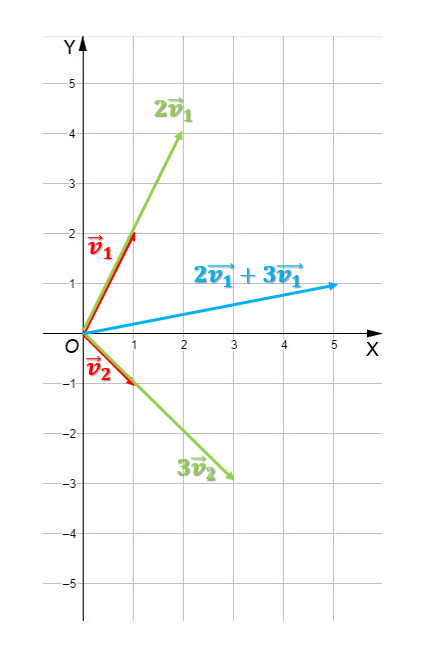
Veamos cómo sería la combinación lineal entre v1 y v2. Lo que haremos es mover el vector 3v2, desplazarlo hasta el final del vector 2v1. Para sumar gráficamente o de forma geométrica los vectores, desplazaríamos el vector de la siguiente forma:
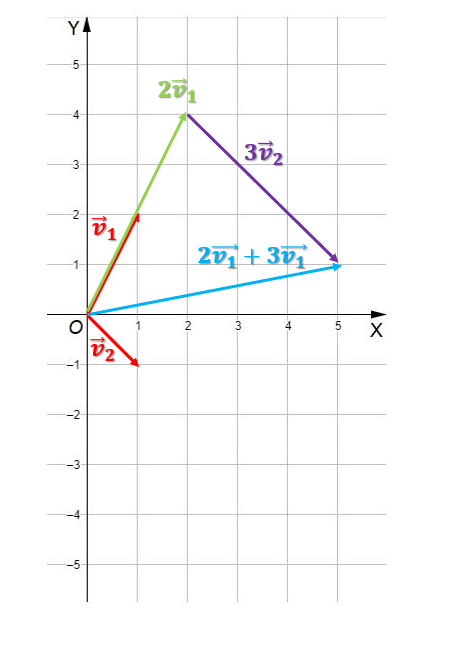
Así pues, tenemos que z es combinación lineal de v1 y v2.
¿Cómo continuar aprendiendo?
Ahora que hemos visto cómo funcionan las combinaciones lineales entre vectores, puedes seguir aprendiendo sobre Big Data, una de las disciplinas con más demandada en la actualidad. Para ello, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que podrás adquirir los conocimientos teóricos y prácticos imprescindibles para entrar en el mercado laboral de manera rápida. No estarás solo, ya que te respaldará nuestro equipo de profesionales, quienes te acompañarán tanto en el proceso formativo como en la búsqueda de empleo siempre que lo necesites. ¡Anímate y solicita más información ahora!







