Hoy vamos a aprender a calcular la desviación típica en Excel, una función clave en estadística, ya que nos ayuda a interpretar datos de manera precisa para que podamos tomar decisiones informadas.

¿Qué es la desviación típica?
Antes de comenzar, resulta fundamental saber con claridad qué es la desviación típica, o como también se conoce, desviación estándar. Si todavía no sabes qué es o te cuesta entenderlo, te lo vamos a explicar de una forma sencilla.
En primer lugar, la desviación típica es una medida que nos indica cuánto varían los valores de un conjunto de datos en relación con su promedio. Por ejemplo, si estás analizando los puntajes de un examen, la desviación típica te dirá si la mayoría de los estudiantes obtuvo resultados cercanos al promedio o si hubo una gran dispersión en las notas.
De esta manera, entre más cercanos al promedio sean los datos, más baja será la desviación típica. Por el contrario, mientras más dispersos estén respecto al promedio, la desviación típica será más alta.
Tomemos el siguiente ejemplo para entenderlo mejor:
Imagina que tienes un conjunto de números, como las edades de los miembros de tu familia. La desviación típica es una medida que nos dice cuánto varían esas edades respecto a la edad promedio de tu familia.
Para calcularlo, primero tenemos que sumar todas las edades y dividir el resultado por el número de personas, con lo que obtendremos la edad promedio. De esta manera, si las edades son 10, 20, 30, y 40, la suma nos dará un total de 100 que, al dividirlo entre 4 los miembros, nos daría un promedio de 25.
Una vez hemos calculado el promedio debemos restar este valor a cada una de las edades, lo que nos dirá cuánto se desvía cada edad del promedio. En nuestro caso, sería de la siguiente manera:
10 menos 25 = -15
20 menos 25 = -5
30 menos 25 = 5
40 menos 25 = 15El siguiente paso entonces será elevar cada una de esas diferencias al cuadrado, para que todos los números sean positivos:
(-15)² = 225
(-5)² = 25
(5)² = 25
(15)² = 225Con esto, debemos sumar los números que nos han resultado y luego dividirlos entre el número de edades menos uno. En nuestro caso, tendríamos que sumar 225 + 25 + 25 + 225 = 500 y luego dividirlo por 3. De esta manera, 500 dividido entre 3 es aproximadamente 166.67.
Finalmente, tomamos la raíz cuadrada de 166.67, lo que nos da aproximadamente 12.91. Este es el valor de la desviación estándar.
Como mencionamos, una desviación estándar más pequeña significa que las edades están más cerca del promedio, es decir, que hay menos variación. Mientras que una desviación más alta significa que las edades están más dispersas respecto al promedio.
¿Cómo calcular la desviación típica en Excel?
Afortunadamente, hoy en día no necesitas ser un experto de estadística para poder realizar este tipo de cálculos, pues contamos con diferentes herramientas que nos ayudan a hacerlos de forma más rápida y práctica. Por esto, vamos ahora a explicarte cómo puedes calcular la desviación típica en Excel.
Como ejemplo, tomaremos las siguientes 10 calificaciones de un grupo de 10 estudiantes:
85, 90, 78, 92, 88, 76, 95, 89, 84, 91En Excel, debemos introducir las calificaciones en una columna, por ejemplo, la columna A. Así, obtendremos los datos en las celdas de A1 a A10. Recuerda que cada calificación debe ir en una celda diferente.
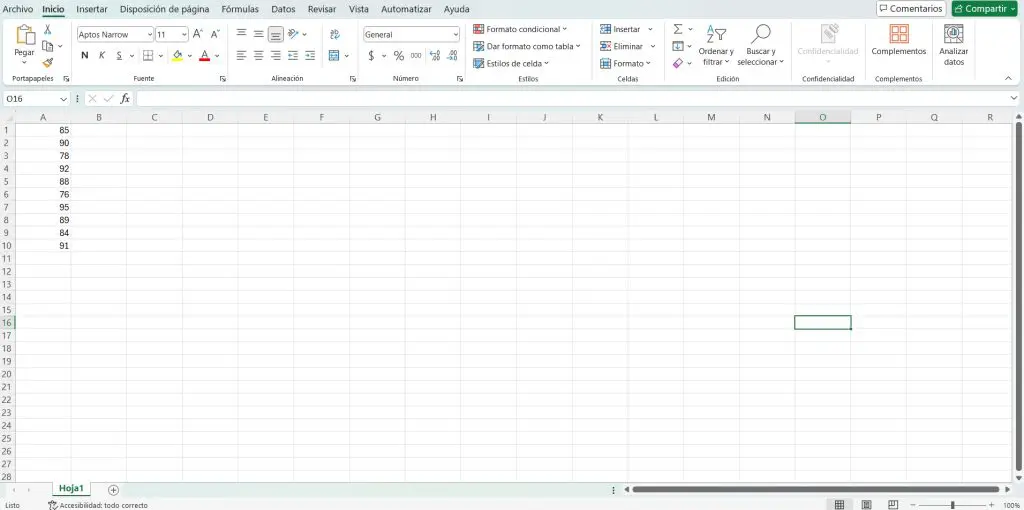
Para el siguiente paso, debemos hacer clic en una celda vacía donde queremos que aparezca el resultado de la desviación estándar. En nuestro caso, tomaremos la celda B1, donde escribiremos la siguiente fórmula de la desviación estándar:
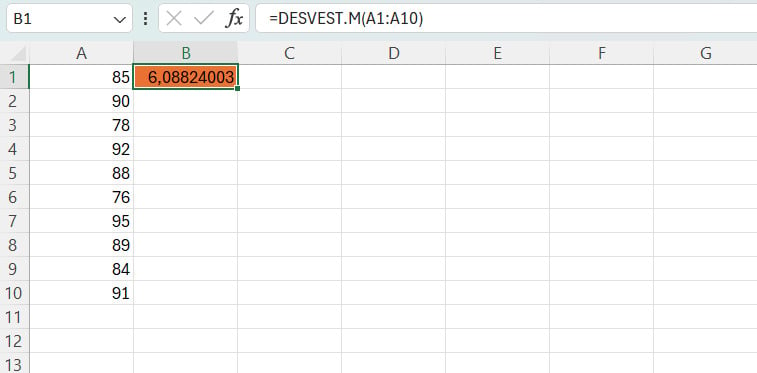
=DESVEST.M(A1:A10)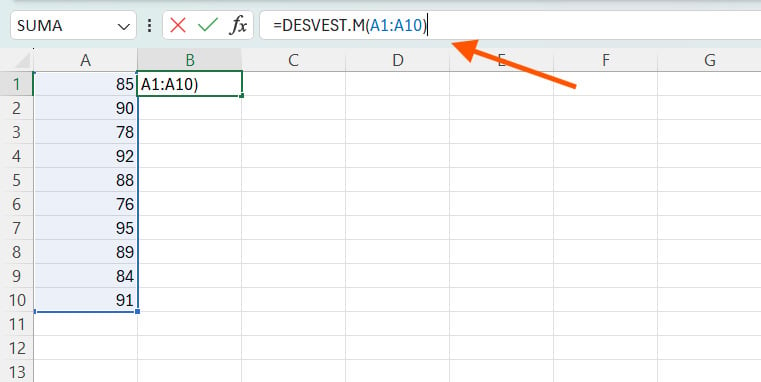
Con esto, la celda B1 nos mostrará el valor de la desviación estándar de las calificaciones de los estudiantes, lo que nos indica cuánto varían las calificaciones respecto a la media.
Tipos de fórmula para calcular la desviación típica en Excel
En Excel, tenemos dos tipos de fórmula que podemos utilizar para calcular la desviación típica según el tipo de datos con el que estamos trabajando.
Desviación Estándar de la Muestra
Esta fórmula es la que debemos usar cuando los datos representan solo una parte del grupo total y queremos hacer inferencias sobre toda la población a partir de esta muestra. Resulta adecuada en estos casos porque ajusta el cálculo para tener en cuenta que estamos trabajando con una muestra, lo que proporciona una estimación más precisa de la variabilidad del grupo completo. La fórmula es la siguiente:
(=DESVEST.M)Desviación Estándar de la Población
Por el contrario, la fórmula de la desviación estándar de la población es la que debemos usar cuando tenemos datos de cada miembro del grupo total, es decir, los datos representan la totalidad de una población:
(=DESVEST.P)¿Vale la pena usar Excel para calcular la desviación típica?
Definitivamente, la respuesta es un sí. Cuando utilizamos Excel para realizar ese tipo de cálculos podemos procesar cientos de datos en apenas unos segundos, lo que requeriría conocimientos avanzados y podría costarnos un enorme esfuerzo si intentáramos hacerlo manualmente. Además, esta herramienta puede proporcionarnos cálculos más precisos, con un margen de error mucho menor que el de los cálculos manuales. Por otro lado, podemos analizar tanto muestras como poblaciones complejas y obtener gráficos y tablas dinámicas que nos brinden un análisis aún más completo.
Si quieres convertirte en un experto en el manejo de datos, en nuestro Bootcamp de Big Data aprenderás a dominar las mejores herramientas y otras tecnologías líderes del sector. Aprende a analizar y visualizar grandes volúmenes de datos para impulsar decisiones estratégicas en cualquier industria.
¡Empieza ahora tu carrera en el mundo del Big Data!











