¿Sabes cómo calcular PCA en R? Sigue leyendo, porque en este artículo te lo explicamos.
Cómo calcular PCA en R
Para calcular PCA en R podemos usar el siguiente comando:
prcomp (mydata)
Este devuelve 3 listas de interés:
- x: aquí se encuentran los datos de la matriz original proyectados sobre los autovectores. Están ordenados de mayor a menor autovalor.
- sdev: es la desviación estándar de cada columna de x. Su cuadrado es el correspondiente autovalor de cov (x).
- rotation: matriz con los autovectores.
#calcular PCA en R
Me <- matrix (c (mydata$x1, mydata$x2), ncol = 2)
print ("Covarianza")
eigen (cov (mydata))[1] «Covarianza»
eigen() decomposition
$values
[1] 24.670594 3.142724
$vectors
| [ , 1 ] | [ , 2 ] | |
| [ 1 , ] | -0.8914069 | 0.4532038 |
| [ 2 , ] | -0.4532038 | -0.8914069 |
#calcular PCA en R
print ("Función prcomp")
prmydata <- prcomp (mydata, center = FALSE, scale. = FALSE)
prmydata[1] «Función prcomp»
Standard deviations (1, .., p = 2):
[1] 4.968667 1.776657
Rotation (n x k) = (2 x 2):
| PC1 | PC2 | |
| x1 | 0.8910839 | -0.4538385 |
| x2 | 0.4538385 | 0.8910839 |
#calcular PCA en R
plot (prmydata$x [ , 1 : 2 ])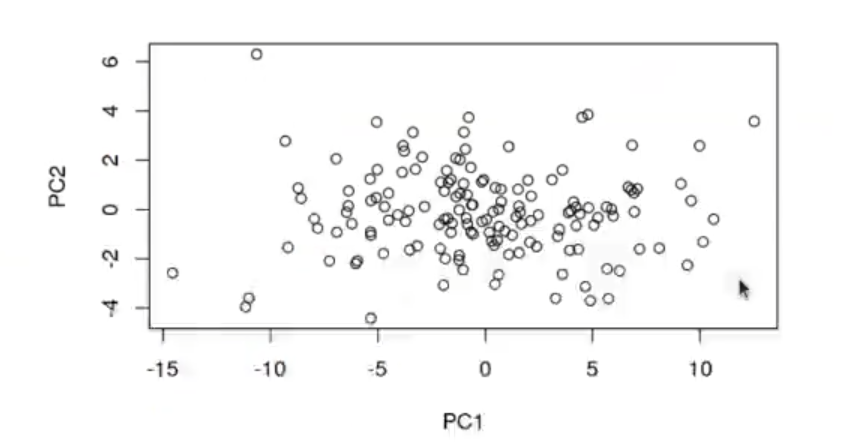
# La matriz de rotación son los autovectores de la matriz de covarianza de los datos originales
prmydata$rotation| PC1 | PC2 | |
| x1 | 0.8910839 | -0.4538385 |
| x2 | 0.4536385 | 0.8910839 |
#calcular PCA en R
cov (prmydata$x)| PC1 | PC2 | |
| x1 | 24.67058345 | -0.01533166 |
| x2 | -0.01533166 | 3.14273523 |
Ejemplo de PCA en R
Vamos a ver un ejemplo de PCA en R con los datos del sol y de la temperatura de varias ciudades.
#calcular PCA en R
df_sunny <- read.csv ('data/cities_sunny.csv')
head (df_sunny)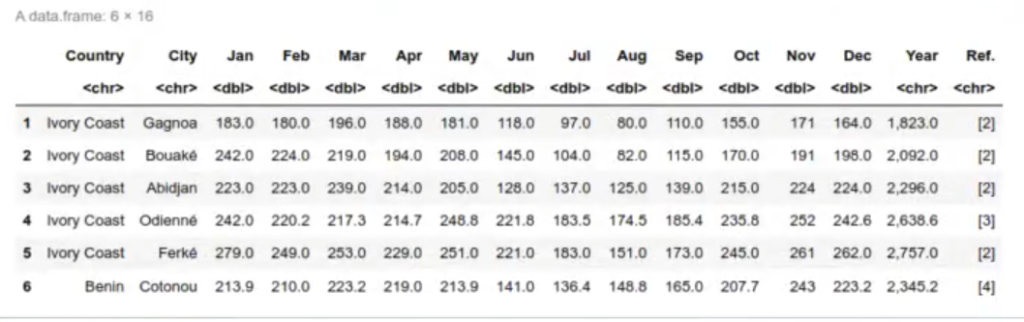
#calcular PCA en R
df_sunny$Year <- NULL
df_sunny$Ref. <- NULL
df_temp <- read.csv ('data/cities_temp.csv')
head (df_temp)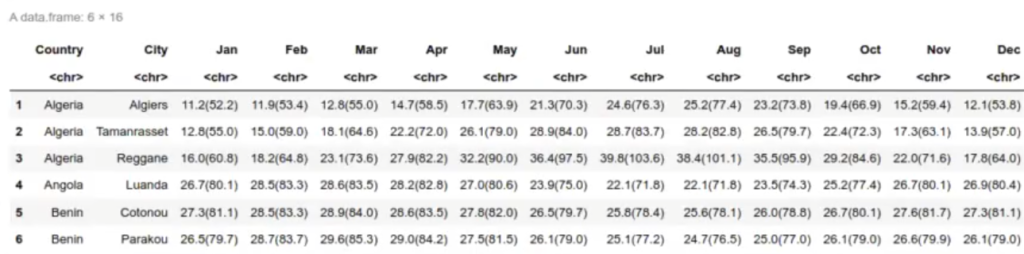
#calcular PCA en R
df_tempsYear <- NULL
df_temp$Ref. <- NULL
library (tidyverse)
#calcular PCA en R
get_celsius <- function (col) {
as.numeric (gsub ( ' - ' , ' - ' , gsub (' \\ ( . * \\ ) ', ' ' , col)))
}
bind_cols (
list (df_temp |>
select (-Country, -City),
df_temp |>
select (-Country, -City) |>
mutate_all (~ get_celsius (.)) )
) -> df_temp
head (df_temp)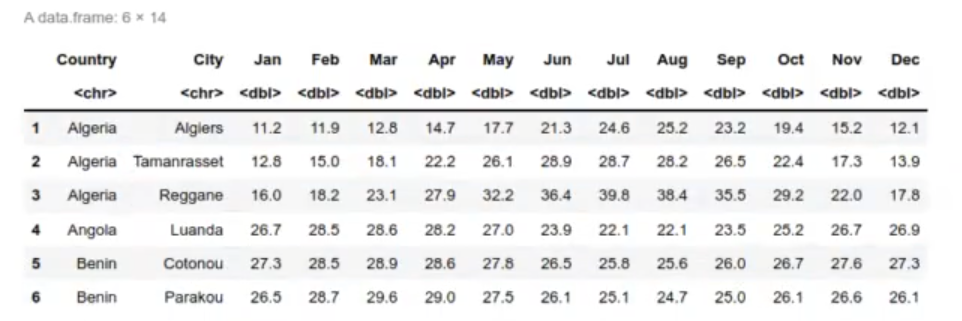
Mostramos el dataframe:
#calcular PCA en R
# https://rpubs.com/williamsurles/293454
df_temp l> inner_join (df_sunny, by = c ('Country, City'), suffix = c ('_ temp', _sun')) -> df_meteo
rownames (df meteo) <- paste (df_meteo$Country, df_meteo$City, sep = ' - ')
df_meteo$City <- NULL
df_meteo$Country <- NULL
str (df_meteo)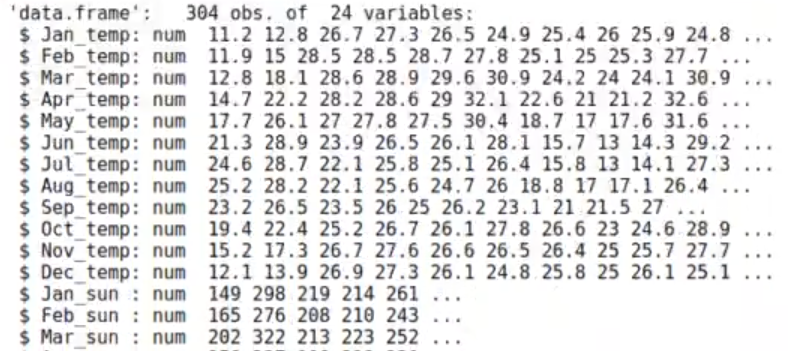
El mismo dataframe, pero en otra presentación, donde el nombre de las filas es el nombre de la ciudad, como podemos observar:
head (df_meteo)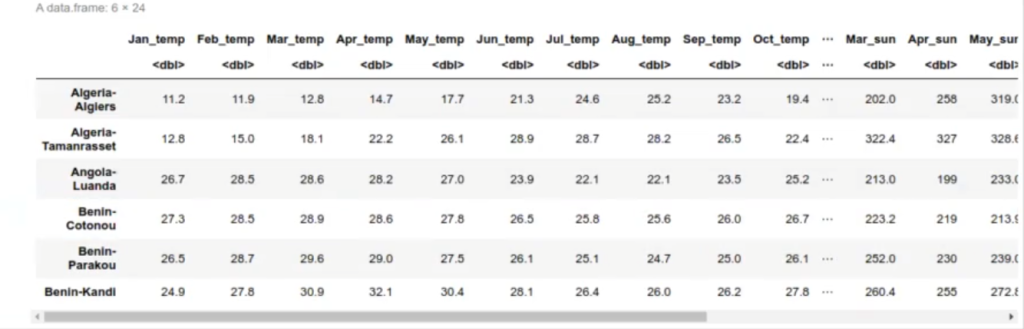
Lo que haremos es intentar calcular PCA en R de esta base de datos.
Tenemos la temperatura de todos los meses, el sol que ha habido a lo largo de los meses.
La correlación entre variables es evidente, porque la temperatura que se tiene en enero es muy similar a la temperatura que se tiene en febrero, en marzo y en algunos otros meses, dependiendo de la época del año. En este último caso, las correlaciones no son tan cercanas. La manera en la que podríamos arreglar esto es dividirlo por estaciones: invierno, verano, otoño y primavera.
El número de variables es alta en este tipo de conjuntos de datos y, por tanto, el análisis de componentes que calcule la matriz de forma predeterminada será alto.
Hasta ahora solo habíamos estado cargando los datos en la matriz de datos, ahora vamos a hacer el análisis de datos.
cord (df_meteo)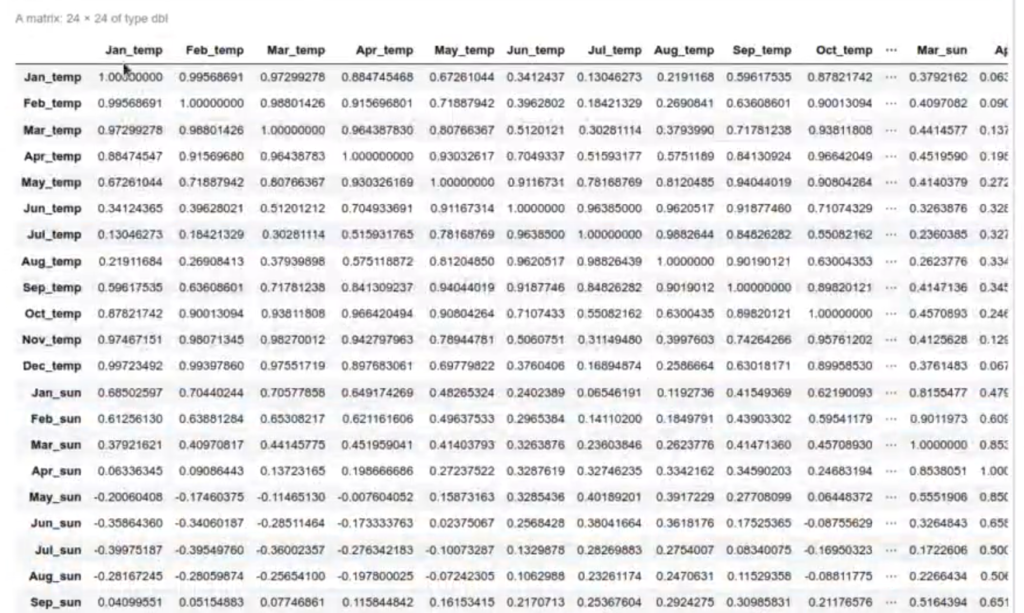
Podríamos hacer todo este proceso de separación manualmente, pero para ello existe una función denominada prcomp, que calcula los componentes principales, lo cual nos da una variable pr_meteo.
pr_meteo <- prcomp (df_meteo, center = TRUE, scale = TRUE)
pr_meteo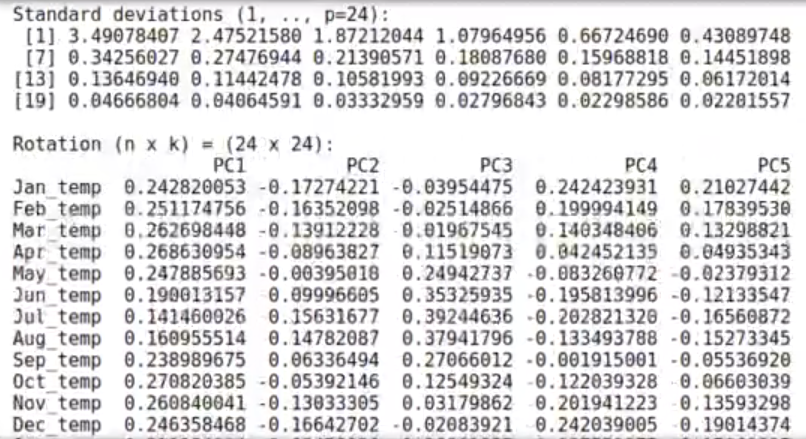
El pr_meteo nos da, las desviaciones estándar de cada uno de los componentes principales; los ha transformado y nos dice cuál es la desviación estándar en cada una de las coordenadas que vamos a tener.
Esto es equivalente al R2 del autovalor.
El pr_meteo también nos brinda la matriz de rotación para cada uno de los componentes.
Si queremos calcular el componente principal 1, lo que tendríamos que hacer es calcular la temperatura en enero y multiplicarla por 0.24, que viene siendo el PC1 de enero; luego, cogemos la temperatura de febrero y la multiplicamos por el PC1 de febrero, que sería 0.25; y así hasta llegar al último mes. Con esto tendríamos el valor de esa ciudad en la componente transformada, o sea, en la PC1.
Aquí no estamos perdiendo ningún tipo de información. Estos componentes podemos transformarlos y detransformarlos cómo y cuándo queramos y sea necesario.
Ahora, miraremos los autovalores normalizados:
plot (pr_meteo$sdev ^ 2 / sum (pr_meteo$sdev ^ 2), main = "Autovalores")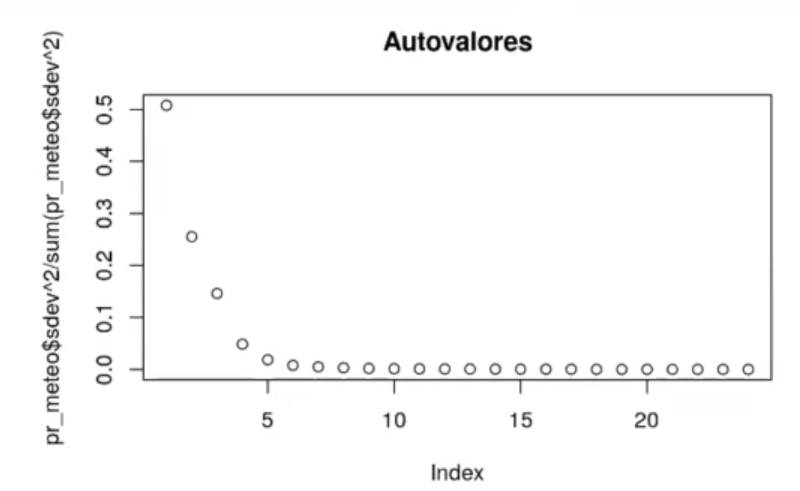
El primer autovalor ya nos dice que hay un 50% de la varianza que está representada en el primer PC1.
A partir del autovalor 5 o 6 ya no hay más información que nos interese, por tanto podemos descargarla.
¿Qué sigue?
Ahora que has visto cómo calcular el PCA en R por medio de un ejercicio con un dataset sobre el clima y el sol, te invitamos a que sigas aprendiendo y, para ello, ponemos a tu disposición nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En pocos meses podrás aprender todo lo necesario para incursionar en el mercado laboral. ¡Solicita más información ahora!











