¿Cómo factorizar paso a paso y sin ser experto en matemáticas? Aprende aquí

Factorizar puede sonar como un término complicado, pero en realidad es una habilidad matemática bastante útil y fácil de aprender, incluso si no eres un experto.

Lo descubrí cuando comencé a enfrentarme a la factorización en mi camino de aprendizaje de álgebra.

Si alguna vez te has encontrado atascado tratando de descomponer un número o una expresión algebraica en factores más simples, este artículo es para ti.

Te explicaré cómo factorizar de manera sencilla, paso a paso, para que puedas aplicar esta técnica en distintos contextos, sin complicaciones.

¿Cómo factorizar? Conoce los 6 métodos de factorización que existen

La factorización es simplemente el proceso de dividir una expresión en factores más simples.

Existen varios métodos, y es útil conocerlos todos para poder elegir el más adecuado según el caso.

Aquí te mostraré los seis métodos más comunes de factorización, con ejemplos prácticos.

Método 1: Factor común

Este es el método más básico y suele ser el primero que aprendes cuando empiezas a estudiar factorización.

El objetivo es encontrar un número o una expresión que se repite en todos los términos de la expresión algebraica.

Pasos:

1. Identifica el factor común en todos los términos de la expresión.
2. Saca ese factor común y ponlo fuera del paréntesis.
3. Lo que queda dentro del paréntesis es el cociente de cada término original dividido entre el factor común.

Ejemplo: Factorizar 6x + 9.

• El factor común es 3, ya que tanto 6 como 9 son divisibles entre 3.
• Sacamos el 3 fuera del paréntesis: 3(2x + 3).

El resultado es 3(2x + 3).

Método 2: Diferencia de cuadrados

Este es un caso especial donde tienes dos términos que son cuadrados perfectos y están separados por una resta. Es una técnica muy útil para factorizar expresiones como a2−b2.

Pasos:

1. Identifica que tienes una diferencia de cuadrados, es decir, una expresión de la forma a2−b2.
2. Aplica la fórmula: (a−b)(a+b).

Ejemplo: Factorizar x2−9.

• x^2 es un cuadrado perfecto (la raíz cuadrada es x).
• 9 es también un cuadrado perfecto (la raíz cuadrada es 3).
• Entonces, aplicamos la fórmula: (x−3)(x+3).

El resultado es (x−3)(x+3).

Método 3: Trinomio cuadrado perfecto

Cuando tienes un trinomio en forma de a2+2ab+b2, puedes factorizarlo como un binomio al cuadrado.

Pasos:

1. Identifica el trinomio en la forma a2+2ab+b2.
2. Aplica la fórmula: (a + b)^2.

Ejemplo: Factorizar x^2 + 6x + 9.

• x^2 es un cuadrado perfecto.
• 9 es un cuadrado perfecto.
• La raíz cuadrada de 9 es 3, y 2ab sería 2×x×3=6x.
• Entonces, la factorización es (x + 3)^2.

El resultado es (x + 3)^2.

Método 4: Trinomio de la forma ax² + bx + c

Este método se utiliza cuando tienes un trinomio cuadrático en la forma ax² + bx + c, donde a, b y c son números.

Pasos:

1. Multiplica a x c.
2. Encuentra dos números que multiplicados den a x c y sumados den b.
3. Descompón el término del medio usando esos dos números.
4. Factoriza por agrupación.

Ejemplo: Factorizar x² +5x+6

• Multiplicamos 1 x 6 = 6.
• Los números que suman 5 y multiplican 6 son 2 y 3.
• Descomponemos 5x como 2x + 3x, lo que da: x² + 2x + 3x + 6.
• Agrupamos: x(x+2)+3(x+2)
• Finalmente, factorizamos (x+2)(x+3).

El resultado es (x+2)(x+3).

Método 5: Factorización por agrupación

Este método se utiliza cuando una expresión tiene más de dos términos, pero puedes agruparlos de manera que cada grupo tenga un factor común.

Pasos:

1. Agrupa los términos de la expresión en dos o más grupos.
2. Factoriza cada grupo.
3. Si el factor común es el mismo en todos los grupos, ponlo fuera del paréntesis.

Ejemplo: Factorizar x² +5x + 6x + 30

• Agrupamos: (x2+5x)+(6x+30)
• Factorizamos cada grupo: x(x+5)+6(x+5)
• Sacamos el factor común: (x+5): (x+5)(x+6)

El resultado es (x+5)(x+6).

Método 6: Factorización por el método de suma y resta de raíces

Este método es más avanzado y se usa principalmente para encontrar las raíces de ecuaciones cuadráticas, aplicando la fórmula general.

Pasos:

• Utiliza la fórmula cuadrática para encontrar las raíces.

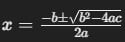
• Escribe el polinomio como el producto de dos binomios utilizando las raíces encontradas.

Ejemplo: Factorizar x² – 5x + 6

• Aplicamos la fórmula cuadrática

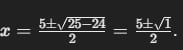
• Las raíces son: x=3x y x=2
• Por lo tanto, la factorización es (x−3)(x−2).

El resultado es (x−3)(x−2).

¿Te gustaría aprender a programar desde cero y aplicar estos conceptos en tus proyectos?

Si te ha interesado este artículo y quieres continuar aprendiendo, el Bootcamp de Programación desde Cero de KeepCoding es el lugar ideal para ti.

Te enseñaremos a programar paso a paso, con ejercicios prácticos que te permitirán aplicar conceptos matemáticos como la factorización en proyectos reales de programación.

¡No pierdas la oportunidad de transformar tu carrera y empezar desde cero con el mejor enfoque práctico!