En este artículo haremos un ejercicio de comparación entre LDA y PCA.
Recordemos que LDA es el acrónimo para Linear discriminant analysis, que quiere decir análisis discriminante linear. Este es un método de clasificación de aprendizaje supervisado en el que dos o más clases son conocidas previamente y nuevas observaciones se clasifican en función de estas, dadas sus características particulares.
El PCA, por su parte, es la sigla correspondiente a Principal component analysis y se traduce como análisis de componentes principales. Es un método que permite simplificar la complejidad de diversos espacios muestrales que poseen múltiples dimensiones, sin perder ningún tipo de información.
¿Qué relación existe entre LDA y PCA?
En PCA también podíamos reducir dimensionalidad, pero al ser agnóstico a la clasificación, no lo hace tan bien cuando tratamos de diferenciar clases etiquetadas previamente:
#LDA y PCA praydata <- prcomp (X) prmydata
Standard deviations (1, .., p = 4):
[1] 2.1157711 0.5012835 0.2789981 0.1561995
Rotation (n x k) = (4 x 4)
| PC1 | PC2 | PC3 | PC4 | |
| Sepal.Length | 0.37583375 | 0.6893993 | 0.54257079 | 0.2977933 |
| Sepal.Width | -0.07314615 | 0.6863192 | -0.66435805 | -0.2867821 |
| Petal.Length | 0.85343419 | -0.1915156 | -0.08587329 | -0.4770719 |
| Petal.width | 0.35362228 | -0.1288512 | -0.50682453 | 0.7755498 |
Tenemos, por tanto, las desviaciones estándar. El primero es un 2, el segundo un 0.5, el tercero es importante y el cuarto incluso podría ser también de relevancia.
El PCA tiene más componentes principales importantes que el LDA y lo que intenta hacer es encontrar diferentes grupos de datos.
#LDA y PCA
iris_train [ , c ("PC1", "PC2")] <- predict (prmydata, newdata = iris_train [ , 1 : 4]) [1 : 2]
ggplot (iris_train, aes (x = PC1, y = PC2, color = Species)) + geom_point ()
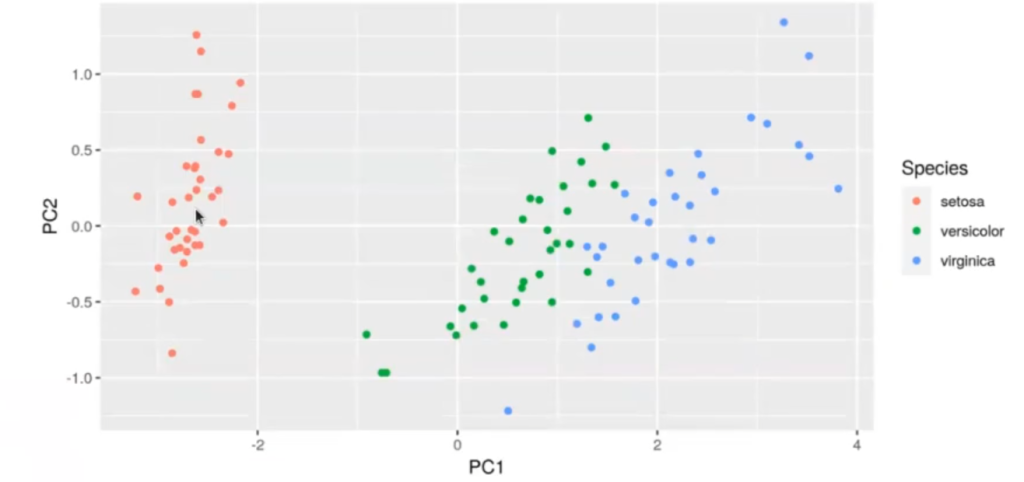
Aquí no podemos decir muy bien cómo separar. Podemos separar el grupo de puntos rojos del grupo de puntos azules y verdes. En cambio, con el LDA es mucho más fácil hacer esta separación:
#LDA y PCA ld_iris <- predict (l, iris_train) df_id_iris <- data.frame (ld_iris$x) df_ld_iris$Species <- iris_train$Species ggplot (df_ld_iris, aes (x = - LD1, y = LD2, color = Species)) + geom_point ()
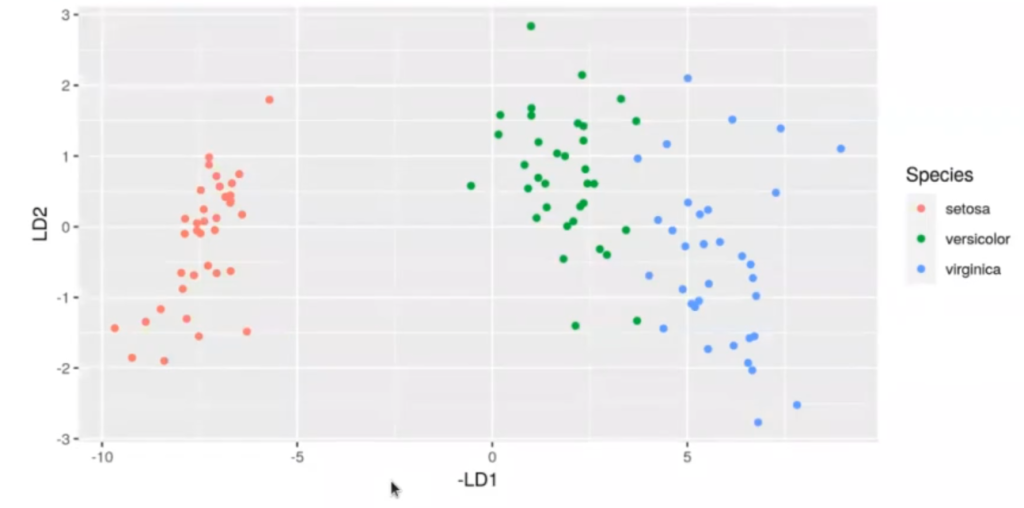
Es más, con esta clasificación solo necesitaríamos una coordenada, la coordenada X. La coordenada Y no nos haría mucha falta; no la tendríamos que usar, aunque podríamos hacerlo.
El LDA, por tanto, se utiliza para clasificación de múltiples clases.
¿Cómo funciona el LDA? El LDA funciona por medio de la proyección de puntos, es decir, de datos, en un plano que tiene tantas dimensiones como clases deseas clasificar, menos 1.
Antes estábamos intentando clasificar entre dos grupos, los grupos A y B, por eso la proyección era una línea. Ahora estamos intentando clasificar entre tres, setosa, virgínica y versicolor, por eso la proyección es de un plano. Si intentáramos clasificar entre 4, la proyección sería en un espacio tridimensional.
El LDA nos dice cuál es el discriminante lineal más importante a la hora de hacer una clasificación. Por ello, nos podríamos cargar los grupos de datos menos importantes, es decir, desecharlos, ya que su covarianza probablemente va a ser de 0.
La diferencia entre el LDA y PCA es que aquí, en el LDA, esto es aprendizaje supervisado. Estamos con un objetivo en mente, que es separar al máximo cada una de las clases. En el PCA el objetivo era diferente, en este el objetivo era separar lo máximo en el eje x la dispersión, y la que no hubiera podido, en el eje que sobresale. El cuarto eje sería otro eje perpendicular a los tres anteriores.
Tenemos, pues, que ambos, el LDA y PCA, pueden usarse para la clasificación. Ambos se pueden usar cuando tenemos múltiples clases, pero en lo que más difieren es en la manera en la que clasifican los datos, ya que mientras el LDA busca clasificar los datos para separar las clases, el PCA clasifica los datos para separarlos y buscar que no existan correlaciones entre ellos, por medio de los autovectores. Este último utiliza, a diferencia del primero, aprendizaje no supervisado.
Ahora que hemos entendido cuál es la diferencia entre LDA y PCA, podemos seguir aprendiendo más sobre data mining. Para ello, KeepCoding te invita a suscribirte al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de solo 8 meses de duración en la que aprenderás conceptos básicos y teoría avanzada y adquirirás todos los conocimientos necesarios para incursionar en el mercado laboral y seguir forjando tu sueño de convertirte en un gran experto en Big Data y sus disciplinas adyacentes. ¡Solicita más información ahora!



