Construcción de un árbol de decisión

El árbol de decisión es una de las herramientas más poderosas para clasificación y modelos predictivos y nos puede ayudar a tomar decisiones complejas en un modelo determinado.

Los árboles de decisión son estructuras que, a pesar de ser fáciles de entender, pueden tener muchos nodos de decisión que aumentan su complejidad en determinados puntos. Por eso, en este artículo, te explicaremos detalladamente la construcción de un árbol de decisión o decision tree.

Árbol de decisión: ¿cómo empezar?

Para construir un árbol de decisión damos inicio con los siguientes pasos:

• Empezamos con el árbol de decisión vacío.
• Seleccionamos la característica sobre la que particionar el espacio (splitting).
  • Regresión: minimizar error cuadrático medio (MSE).
  • Clasificación:
    • Mínimo error de clasificación.
    • Mínima impureza.
    • Máxima entropía.
• Para cada región resultante repetimos el proceso (recursive splitting), hasta que se cumpla un criterio de parada:
  • Todas las muestras con única variable target (y).
  • Complejidad:
    • Profundidad.
    • Número de muestras en hoja.
    • Mejora en el criterio de splitting.

Métricas de clasificación

Tratamos con un problema de clasificación con K categorías. En el nodo m se define p_km como la proporción de observaciones de entrenamiento en dicho nodo para la clase k.

• Error de clasificación: E (X_m) = 1 — max {p_km }
• Índice Gini: G (X_m) = ∑ p_km (1 — p_km) = 1 — ∑ (p_km)²
• Entropía: D (X_m) = — ∑ p_km (log (p_km))

Donde X_m son los datos de entrenamiento en en nodo m.

Un ejemplo sencillo de árbol de decisión

Veamos un ejemplo simple donde podemos aplicar un árbol de decisión:

Label	Var1	Var2
A	0	33
A	0	54
A	0	56
A	0	42
A	1	50
B	1	55
B	1	31
B	0	-4
B	1	77
B	0	49

¿Por qué variable particionamos el árbol?

Tenemos dos hipótesis:

• Var1 == 1
• Var2 >= 32

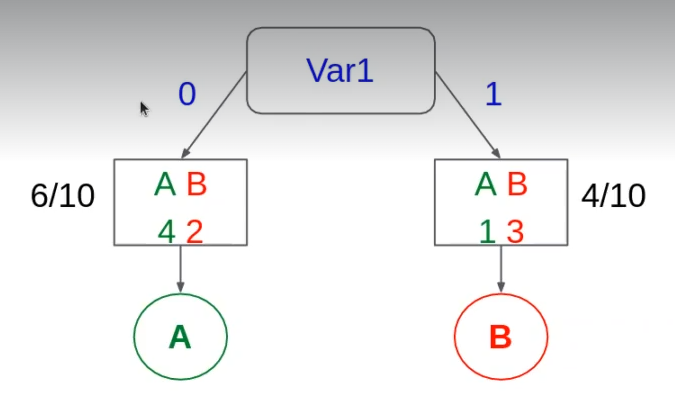
Veamos el primer caso, la variable1 (Var1). Tenemos que Var1 puede ser igual a cero o a uno (variable binaria). Entonces:

• Var1 = 0
  • Tenemos una división de la variable target: tenemos 6 muestras de 10 (6/10), de las cuales 4 son A y 2 son B. Así, concluiríamos que el voto mayoritario es por A.

Ahora veamos cuál es el error de G para el lado izquierdo (Var1 = 0) es:

G_LEFT = 1 – [(4 / 6)² + (2 / 6)²] = 0.444

E_LEFT = 1 – max {4 / 6, 2 / 6} = 2 / 6 = 1 / 3

• Var1 = 1
  • Tenemos, al igual que en el caso anterior, una división de la variable target: tenemos 4 muestras de 10 (4/10), de las cuales 1 es A y 3 son B. De modo que el voto mayoritario sería por B.

El error de G para el lado derecho (Var1 = 1)

G_RIGHT = 1 – [(1 / 4)² + (3 / 4)²] = 0.375

E_RIGHT = 1 – max {1 / 4, 3 / 4} = 1 / 4

Ahora veamos cuál es el error total:

G_TOTAL = 6 / 10 * 0.44 + 4 / 10 * 0.375 = 0.41667

E_TOTAL = 6 / 10 * 1 / 3 + 4 / 10 * 1 / 4 = 3 / 10 = 0.3

El árbol de decisión habría terminado aquí y el error de G habría sido 0.41667, mientras que el error de clasificación habría sido 0.3.

Ahora podemos hacer lo mismo con el segundo caso, la variable 2 (Var2). Al igual que Var1, esta variable también es binaria, así que se procede del mismo modo y el resultado es:

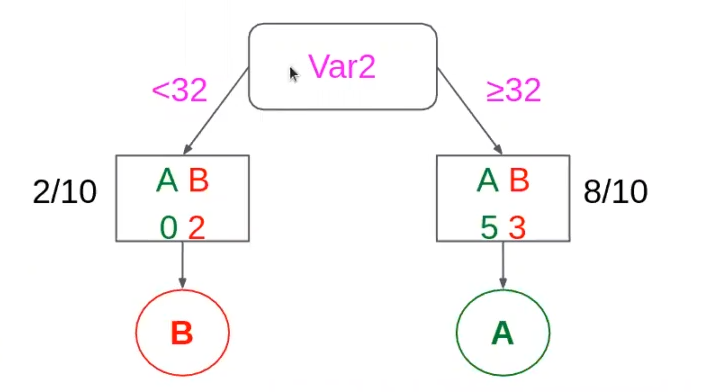
G_LEFT = 1 – [(0 / 2)² + (2 / 2)²] = 0

E_LEFT = 1 – max {0 / 2, 2 / 2} = 0

G_RIGHT = 1 – [(5 / 5)² + (3 / 8)²] = 0.469

E_RIGHT = 1 – max {5 / 8, 3 / 8} = 3 / 8

G_TOTAL = 2 / 10 * 0 + 8 / 10 * 0.469 = 0.375

E_TOTAL = 2 / 10 * 0 + 8 / 10 * 3 / 8 = 3 / 10 = 0.3

Si lo comparamos con la variable anterior y de estar usando G, la Var2 sería la mejor, porque el error de G en esta variable es menor.

Así, concluiríamos que, de las dos hipótesis planteadas en el inicio:

• Var1 == 1
• Var2 >= 32

De este modo continuaríamos construyendo el árbol de decisión hasta cumplir el criterio de parada.

¿Qué sigue?

Ahora que hemos visto cómo funciona un árbol de decisión, podemos dar paso a aprender otros conceptos, como el random forest o los boosted trees. Si quieres seguir formándote en estas temáticas que pertenecen a un área que está siendo top en este momento en el mercado laboral, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el cual aprenderás todo lo necesario para incursionar en el interesante mundo IT. ¡No esperes más y solicita información ahora!