Cuando empecé a estudiar probabilidad, una de mis mayores frustraciones fue encontrar información dispersa. Cada fuente parecía enfocarse en un aspecto diferente, y al final, tenía que visitar varias webs para obtener un panorama completo. Por eso, en este artículo he reunido todo lo que necesitas saber sobre las leyes de probabilidad, explicándolas de manera clara y con ejemplos prácticos.
¿Qué son las leyes de probabilidad?
Las leyes de probabilidad son reglas matemáticas que nos permiten calcular la posibilidad de que ocurra un evento. Se usan en estadística, matemáticas, inteligencia artificial y hasta en decisiones cotidianas, como evaluar riesgos en inversiones o determinar la probabilidad de lluvia.
Según el libro Probability and Random Processes de Grimmett y Stirzaker, estas leyes son la base fundamental del cálculo de probabilidades y sus aplicaciones en diversas áreas del conocimiento.

Principales leyes de probabilidad
A continuación, te presento las leyes fundamentales de la probabilidad con ejemplos prácticos:
1. Ley de la suma
Si tenemos dos eventos A y B, la probabilidad de que ocurra A o B (o ambos) se calcula así:
P(A∪B)=P(A)+P(B)−P(A∩B)
Ejemplo: Si la probabilidad de que llueva mañana es 30% y la probabilidad de que haya viento fuerte es 40%, y sabemos que la probabilidad de que ocurran ambos eventos es 15%, entonces:
P(lluvia∪viento)=0.3+0.4−0.15=0.55
Es decir, hay un 55% de probabilidades de que ocurra al menos uno de los dos eventos.
Más sobre probabilidad en el clima
2. Ley del complemento
Nos dice que la probabilidad de que un evento NO ocurra es:
P(Ac)=1−P(A)
Ejemplo: Si la probabilidad de ganar un sorteo es 0.2 (20%), la probabilidad de no ganar es:
P(Noganar)=1−0.2=0.8(80
3. Ley de la multiplicación
Si queremos calcular la probabilidad de que dos eventos A y B ocurran simultáneamente, usamos:
P(A∩B)=P(A)×P(B∣A)
Si los eventos son independientes:
P(A∩B)=P(A)×P(B)
Ejemplo: Si la probabilidad de que un estudiante apruebe matemáticas es 0.7 y la probabilidad de que apruebe estadística, dado que aprobó matemáticas, es 0.8, entonces:
P(Apruebaambas)=0.7×0.8=0.56(56
4. Ley de Bayes
Es fundamental en inteligencia artificial y máquinas de aprendizaje. Nos permite actualizar la probabilidad de un evento en función de nueva información:
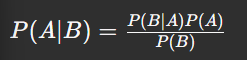
Ejemplo: Si la probabilidad de tener una enfermedad es 1% y la prueba diagnóstica tiene una tasa de falsos positivos del 5%, la probabilidad real de estar enfermo dado un resultado positivo no es tan alta como podría parecer. Ahí es donde Bayes nos ayuda a calcularlo con mayor precisión.
¿En qué campos podemos aplicar las leyes de probabilidad?
Las leyes de probabilidad no solo se usan en matemáticas, sino también en:
- Inteligencia artificial y machine learning: Predicciones de comportamiento, recomendaciones en plataformas de streaming, etc.
- Finanzas y economía: Evaluación de riesgos en inversión y seguros.
- Medicina: Diagnóstico de enfermedades y pruebas de laboratorio.
- Juegos de azar: Análisis de probabilidades en casinos y apuestas.
Si te interesa aplicar estos conocimientos en un campo con alta demanda profesional, te invito a conocer nuestro Bootcamp en Big Data y Machine Learning en KeepCoding. En él, aprenderás a utilizar técnicas avanzadas de análisis de datos y modelos predictivos basados en probabilidad para resolver problemas del mundo real. ¡No te quedes atrás y da el siguiente paso en tu formación!











