La definición de inversa de una matriz forma parte de la serie de cálculos utilizados para llevar a cabo un análisis estadístico de los macrodatos. Comprender cómo se desarrolla te resultará muy útil y no te llevará demasiado tiempo; por ello, en este post, te explicamos cómo se produce la definición de inversa de una matriz para el manejo Big Data.
Definición de inversa de una matriz
La definición de inversa de una matriz hace referencia a una matriz cuadrada A que se escribe A-1 y se define como:
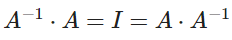
En la que la I es la matriz identidad, por lo que:
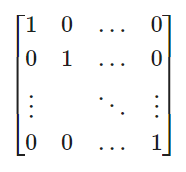
Por ejemplo
A continuación, te compartimos un ejemplo aleatorio para que comprendas mejor cómo funciona la definición de inversa de una matriz.
A<-matrix(c(1,3,5,2,3,4,1,7,8),nrow=3)
print("Tenemos una matriz A:")
A
[1] «Tenemos una matriz A:»
A matrix: 3 × 3 of type dbl
| 1 | 2 | 1 |
| 3 | 3 | 7 |
| 5 | 4 | 8 |
print("La inversa de A es:")
iA<-solve(A)
iA
[1] «La inversa de A es:»
A matrix: 3 × 3 of type dbl
| -0.2666667 | -0.8 | 0.7333333 |
| 0.7333333 | 0.2 | -0.2666667 |
| -0.2000000 | 0.4 | -0.2000000 |
print("Si multiplicamos una matriz por su inversa obtenemos una matriz identidad")
iA %*% A
[1] «Si multiplicamos una matriz por su inversa obtenemos una matriz identidad»
A matrix: 3 × 3 of type dbl
| 1.000000e+00 | 0 | -8.881784e-16 |
| -1.665335e-16 | 1 | 0.000000e+00 |
| -1.665335e-16 | 0 | 1.000000e+00 |
Resolver ecuaciones
Una de sus grandes ventajas es que podrás usar la matriz inversa para resolver ecuaciones según la siguiente guía:
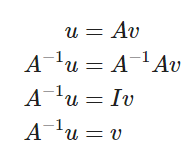
De manera que su desarrollo se da de la siguiente forma:
print("Calculamos el vector u como resultado de multiplicar A·v")
v <- c(1,2,3)
u <- A %*% v
u
[1] «Calculamos el vector u como resultado de multiplicar A·v»
A matrix: 3 × 1 of type dbl
8
30
37
print("Comprobamos que multiplicando u por la inversa de A obtenemos v de vuelta:")
iA %*% u
[1] «Comprobamos que multiplicando u por la inversa de A obtenemos v de vuelta:»
A matrix: 3 × 1 of type dbl
1
2
3
En este post te hemos explicado este tipo de cálculo para el manejo estadístico de tus macrodatos. Sin embargo, ¡todavía queda mucho por aprender!
Te impulsamos a seguir formándote sobre muchas más herramientas dentro del manejo del Big Data, como Data Mining, Scala y Spark o Machine Learning 101, entre otras. Gracias a nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning podrás lograr esto y más. ¡Échale un vistazo!



