Los tensores son de suma importancia para el desarrollo de este tipo de campo en el manejo de los macrodatos. Por ello, en este post, te exponemos la definición de tensores en Deep Learning.
Definición de tensores en Deep Learning
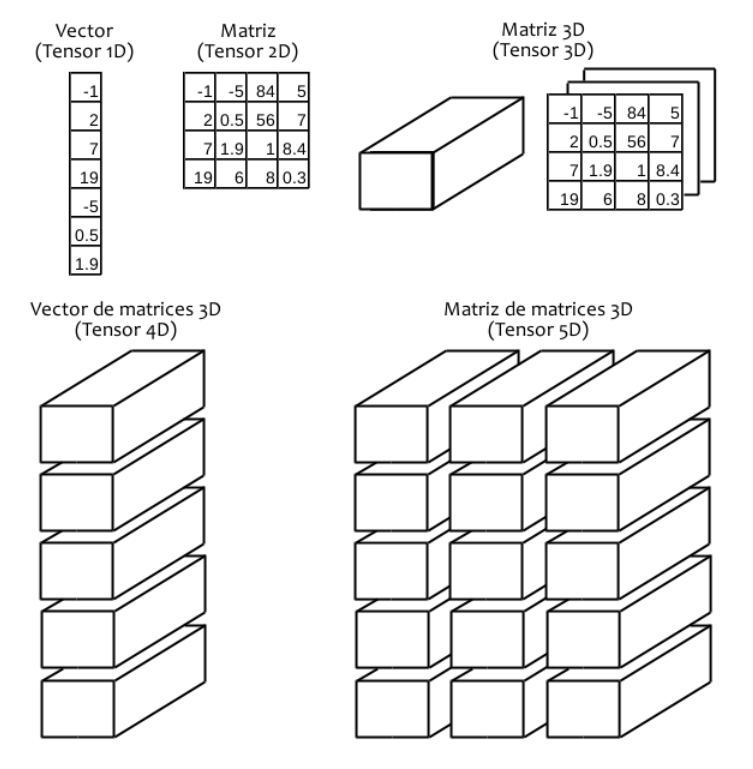
Aunque la definición de tensores en Deep Learning la inventaron los físicos para ser capaces de describir interacciones, en el ámbito de la IA se pueden entender como contenedores de números.
Práctica con la definición de tensores en Deep Learning
Para entender cómo funciona la definición de tensores en Deep Learning, te exponemos una sólida práctica:
import numpy as np
import tensorflow as tf
# Imaginaos que queréis guardar la nota media del máster de Tristina Cipuentes.
# Para ello utilizaríais un tensor de 0D, que no es otra cosa que un simple
# número, también conocido como escalar.
# Tensor 0D
arr0d = np.array(5)
tensor_0D = tf.convert_to_tensor(arr0d,tf.float64)
# De este escalar, podemos ver tanto su contenido como ciertas propiedades
print("Nota media:{}".format(arr0d))
print("Dimensiones del tensor: {}".format(tensor_0D.ndim))
print("Tamaño del tensor: {}".format(tensor_0D.shape))
print("Tipo del tensor: {}".format(tensor_0D.dtype))
Nota media:5
Dimensiones del tensor: 0
Tamaño del tensor: ()
Tipo del tensor:
# Pero con una sola nota no habría mucho que defender, podría decirse incluso
# que alguien se la ha inventado, así que mejor si guardamos las notas de
# TODOS las asignaturas que hizo. Podemos usar un tensor 1D para ello:
# Tensor 1D (vector)
array_1D = np.array([2, 8, 6])
tensor_1D = tf.convert_to_tensor(array_1D,tf.float64)
print("Notas de las asignaturas: {}".format(tensor_1D))
print("Dimensiones del tensor: {}".format(tensor_1D.ndim))
print("Tamaño del tensor: {}".format(tensor_1D.shape))
print("Tipo del tensor: {}".format(tensor_1D.dtype))
Notas de las asignaturas: [2 8 6]
Dimensiones del tensor: 1
Tamaño del tensor: (3,)
Tipo del tensor: int64
# Un momento... ¿no sería mejor que estructurásemos las notas por asignatura?
# ¿Cómo podríamos hacerlo, si cada asignatura consta de 3 exámenes?
# ¡Con un tensor 2D! ¡ Una matriz de números!
# Tensor 2D (matriz)
array_2D = np.array([[0, 1, 1], # asignatura 1
[2, 3, 3], # asignatura 2
[1, 3, 2]]) # asignatura 3
tensor_2D = tf.convert_to_tensor(array_2D,tf.float64)
print("Las puntuaciones de Tristina en sus exámenes son:\n{}".format(tensor_2D))
print("Asignatura 1:\n{}".format(tensor_2D[0]))
print("Asignatura 2:\n{}".format(tensor_2D[1]))
print("Asignatura 3:\n{}".format(tensor_2D[2]))
print("Dimensiones del tensor: {}".format(tensor_2D.ndim))
print("Tamaño del tensor: {}".format(tensor_2D.shape))
print("Tipo del tensor: {}".format(tensor_2D.dtype))
Las puntuaciones de Tristina en sus exámenes son:
[[0 1 1]
[2 3 3]
[1 3 2]]
Asignatura 1:
[0 1 1]
Asignatura 2:
[2 3 3]
Asignatura 3:
[1 3 2]
Dimensiones del tensor: 2
Tamaño del tensor: (3, 3)
Tipo del tensor: int64
# Sin embargo, como nosotros somos muy ordenados y no queremos que se nos pierda
# nada, mejor guardamos las notas de las asignaturas (que son anuales) por
# cuatrimestres, así será más fácil acceder a ellas si hiciese falta en un futuro.
# Para eso, podemos añadir una dimensión a nuestro tensor 2D que indique el cuatrimestre.
# Tensor 3D (matriz 3D o cubo)
array_3D = np.array([[[0, 1, 1], # Primer cuatrimestre
[2, 3, 3],
[1, 3, 2]],
[[1, 3, 2], # Segundo cuatrimestre
[2, 4, 2],
[0, 1, 1]]])
tensor_3D = tf.convert_to_tensor(array_3D,tf.float64)
print("Las notas de Tristina por cuatrimestre son:\n{}".format(tensor_3D))
print("Primer cuatrimestre:\n{}".format(tensor_3D[0]))
print("Segundo cuatrimestre:\n{}".format(tensor_3D[1]))
print("Dimensiones del tensor: {}".format(tensor_3D.ndim))
print("Tamaño del tensor: {}".format(tensor_3D.shape))
print("Tipo del tensor: {}".format(tensor_3D.dtype))
Las notas de Tristina por cuatrimestre son:
[[[0 1 1]
[2 3 3]
[1 3 2]]
[[1 3 2]
[2 4 2]
[0 1 1]]]
Primer cuatrimestre:
[[0 1 1]
[2 3 3]
[1 3 2]]
Segundo cuatrimestre:
[[1 3 2]
[2 4 2]
[0 1 1]]
Dimensiones del tensor: 3
Tamaño del tensor: (2, 3, 3)
Tipo del tensor: int64
# Ya tenemos guardadas las notas de Tristina, para que no se pierdan.
# ¿Pero qué pasa con los demás alumnos? Para guardar también sus
# notas podemos añadir una dimensión a nuestro tensor. Así podemos
# tener las notas por cuatrimestre de cada asignatura para cada alumno.
# Tensor 4D (vector de matrices 3D o vector de cubos)
array_4D = np.array([[[[0, 1, 1], # Tristina
[2, 3, 3],
[1, 3, 2]],
[[1, 3, 2],
[2, 4, 2],
[0, 1, 1]]],
[[[0, 3, 1], # Facundo
[2, 4, 1],
[1, 3, 2]],
[[1, 1, 1],
[2, 3, 4],
[1, 3, 2]]],
[[[2, 2, 4], # Celedonio
[2, 1, 3],
[0, 4, 2]],
[[2, 4, 1],
[2, 3, 0],
[1, 3, 3]]]])
tensor_4D = tf.convert_to_tensor(array_4D,tf.float64)
print("Las notas de Tristina, Facundo y Celedonio por cuatrimestre son:\n{}".format(tensor_4D))
print("Notas de Tristina:\n{}".format(tensor_4D[0]))
print("Notas de Facundo:\n{}".format(tensor_4D[1]))
print("Notas de Celedonio:\n{}".format(tensor_4D[2]))
print("Dimensiones del tensor: {}".format(tensor_4D.ndim))
print("Tamaño del tensor: {}".format(tensor_4D.shape))
print("Tipo del tensor: {}".format(tensor_4D.dtype))

En este ejemplo de definición de tensores en Deep Learning, las notas de Tristina, Facundo y Celedonio por cuatrimestre son:
[[[[0 1 1]
[2 3 3]
[1 3 2]]
[[1 3 2]
[2 4 2]
[0 1 1]]]
[[[0 3 1]
[2 4 1]
[1 3 2]]
[[1 1 1]
[2 3 4]
[1 3 2]]]
[[[2 2 4]
[2 1 3]
[0 4 2]]
[[2 4 1]
[2 3 0]
[1 3 3]]]]
Notas de Tristina:
[[[0 1 1]
[2 3 3]
[1 3 2]]
[[1 3 2]
[2 4 2]
[0 1 1]]]
Notas de Facundo:
[[[0 3 1]
[2 4 1]
[1 3 2]]
[[1 1 1]
[2 3 4]
[1 3 2]]]
Notas de Celedonio:
[[[2 2 4]
[2 1 3]
[0 4 2]]
[[2 4 1]
[2 3 0]
[1 3 3]]]
Dimensiones del tensor: 4
Tamaño del tensor: (3, 2, 3, 3)
Tipo del tensor: int64
Así podríamos seguir hasta el infinito, añadiendo dimensiones a los tensores para ser capaces de guardar más datos. Para entender cómo funciona la definición de tensores en Deep Learning:
- Tensores 3D: utilizados en series temporales.
- Tensores 4D: utilizados con imágenes.
- Tensores 5D: utilizados con vÍdeos.
Si quieres profundizar en la Definición de tensores en Deep Learning o más ejemplos, aquí tienes un recurso muy bueno para ello.
Aprende más sobre el Big Data
En este post, te hemos expuesto la definición de tensores en Deep Learning, sin embargo, si quieres aprender más sobre el Big Data, desde KeepCoding te brindamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Al finalizar, en menos de nueve meses, serás capaz de reconocer las ventajas e inconvenientes de los distintos programas estudiados. ¡Inscríbete!











