Aplicar el descenso de gradiente para regresión lineal no tiene ninguna complejidad. Nuestro modelo viene dado por la siguiente ecuación:
f (x) = w0 + wT x
Debemos optimizar esa función para encontrar los valores de w que la hacen mínima, pero ¿cómo medimos qué la hace mínima y qué no?
Descenso de gradiente para regresión lineal
A continuación vamos a ver el descenso de gradiente para regresión lineal.
El descenso de gradiente viene dado por la expresión xi = xi-1 — η . ▽ f (x). Esta expresión lo único que indica es la lógica con la que hemos explicado el término de gradient descent por medio de la bajada de una montaña.
Entonces, para aplicar descenso de gradiente para regresión lineal, y así optimizar la función, lo que debemos y pretendemos hacer es hacer mínima la distancia que hay entre el punto (color rojo) y el plano (escala de colores azul – amarillo, como se observa en la imagen). Es decir, queremos que el modelo esté muy cerca de los puntos de nuestros datos.
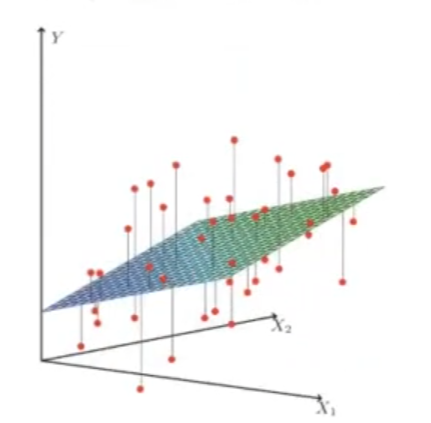
Para optimizar una función de descenso de gradiente para regresión lineal debemos usar el Residual sum squares (RSS), que mide cuánto se aleja el modelo de los valores reales.
¿Pero esto no es lo mismo que least squares? Sí y no. Least squares es un método para construir un modelo y RSS es una medida. Aunque sí se basan en lo mismo, en medir la distancia entre los valores predichos y los valores verdaderos.
Aplicamos RSS a nuestra regresión:
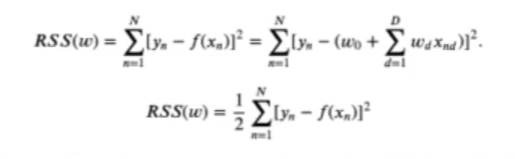
Esto se hace midiendo el cuadrado de la diferencia de nuestros datos, es decir, se puede hacer con la fórmula arriba propuesta.
La ecuación de mínimos cuadrados nos permite obtener los parámetros. Aquí lo que estamos usando es esa medida, que es el residual sum squares, la suma de los cuadrados de los errores para desarrollar la ecuación que nos permite usar el gradiente descendente y calcular los parámetros.
Esta ecuación se podría resumir del siguiente modo: se suman todos los errores, luego se va a coger cada punto y se va a calcular su distancia respecto a la solución del modelo; la solución clara del modelo es f (xn). Posteriormente, restamos y lo igualamos al cuadrado, exactamente igual, para que sea convexo.
Entonces, f (xn) no es más que la ecuación de la regresión lineal que hemos visto antes, porque es nuestro modelo y esta ecuación nos va a dar el output del modelo, es decir, lo que predice.
La finalidad de todo esto es hacer que el error que estamos midiendo sea lo más pequeño posible y que se acerque todo lo que pueda a nuestro dataset.
Lo que queremos es minimizar esta distancia para que el modelo se acerque lo máximo posible a los valores verdaderos.
Para hacer que el error sea pequeño, tenemos la siguiente expresión:
▽RSS (w) = XT (Xw2 — y)
Introducimos la ecuación en el gradiente descendente. El gradiente descendente es un método de optimización, una herramienta que usamos para obtener los valores que hacen mínima una función. ¿Qué es lo que queremos hacer mínimo? Pues el error; el error no es más que la expresión XT (Xw2 — y). Esta expresión deriva de la primera.
¿Y por qué queremos minimizar el error? Esto se debe a que queremos que nuestro modelo se acerque mucho a los datos de entrenamiento que le demos, ya que esto permitirá que el modelo funcione bien.
Para encontrar los parámetros que hacen mínima esa función, es decir, los parámetros del plano, que reduce muchísimo el error, usamos una herramienta de optimización, que en este caso es el descenso de gradiente para regresión lineal.
En resumen, el descenso de gradiente para regresión lineal está basado en resolver esta ecuación de forma iterativa:
w2+1 = w2 — η * ▽RSS (w)
Al final, de lo que trata el descenso de gradiente para regresión lineal es de introducir la segunda ecuación en esta última, que corresponde a la tercera.
Si quieres seguir aprendiendo, podrás acceder a una de las disciplinas más demandadas y con mejores sueldos de todo el mercado laboral en pocos meses con la guía del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra y de gran intensidad en la que adquirirás todos los conocimientos imprescindibles para obtener el trabajo de tus sueños en el sector IT. ¡Entra ya para solicitar información e impulsa tu carrera!











