Diferencia de cuadrados perfectos: Explicación y ejemplos clave

Cuando me preguntan sobre la diferencia de cuadrados perfectos, siempre pienso en cómo esta sencilla fórmula puede abrir muchas puertas para entender y dominar el álgebra. En este artículo compartiré contigo no solo qué es y cómo usar la diferencia de cuadrados perfectos, sino también trucos prácticos y ejemplos que he encontrado útiles en mi experiencia enseñando matemáticas.

¿Qué es la diferencia de cuadrados perfectos? Explicación clara y sencilla

Para empezar, ¿qué significa realmente la diferencia de cuadrados perfectos? En matemáticas, se refiere a una expresión algebraica que tiene la forma:
a² – b²
donde a y b pueden ser números, variables o incluso expresiones algebraicas, pero siempre elevados al cuadrado. El elemento clave aquí es la resta (diferencia) entre estos dos cuadrados.

Este tipo de expresión es muy especial, porque posee una propiedad única que permite factorizarla de forma rápida y eficiente, algo que no siempre es fácil en álgebra.

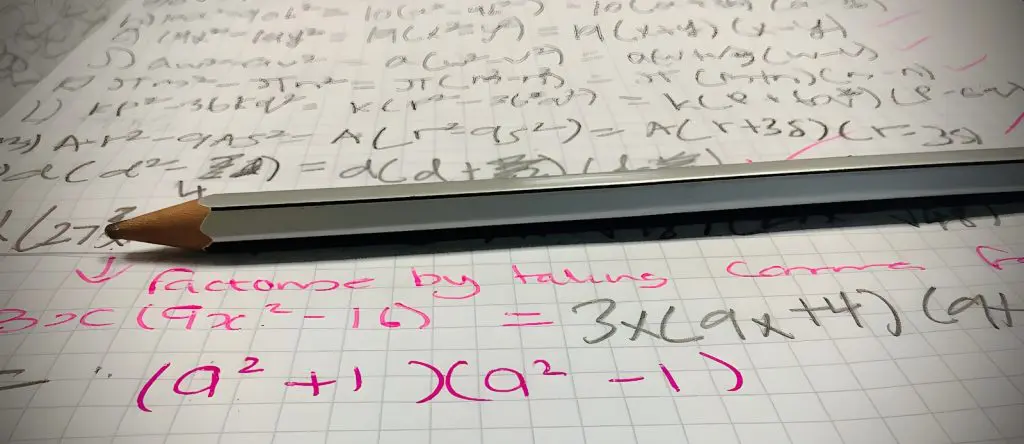
La fórmula fundamental: cómo factorizar la diferencia de cuadrados perfectos

Desde el primer momento en que aprendí esta fórmula, supe que era una herramienta fundamental para resolver problemas rápidos. La identidad algebraica que define la diferencia de cuadrados perfectos es:
a² – b² = (a – b)(a + b)

Esto significa que si tienes la resta entre dos términos que son cuadrados perfectos, puedes factorizarla multiplicando la diferencia de sus raíces cuadradas por la suma de las mismas.

Cómo reconocer una diferencia de cuadrados perfectos: pasos prácticos

No siempre es sencillo identificar esta fórmula en problemas más complejos. Aquí te doy algunas pautas que siempre reviso:

1. Verifica que ambos términos sean cuadrados perfectos:
   Ejemplo:
   • 16 = 4², es un cuadrado perfecto.
   • 25x² = (5x)², también es cuadrado perfecto, porque la variable está elevada al cuadrado.
2. Comprueba que entre los dos términos haya una resta (-), no una suma (+).
3. Los términos pueden contener variables, pero siempre con exponentes pares que correspondan a un cuadrado.

Si ambos puntos se cumplen, estás ante una diferencia de cuadrados perfectos.

Ejemplos reales que te ayudarán a dominar la diferencia de cuadrados perfectos

En mi experiencia, enseñar con casos prácticos es fundamental. Aquí te dejo ejemplos variados para consolidar la comprensión:

Ejemplo 1: Expresión sencilla

Factoriza:
x² – 36

Solución:
Ambos términos son cuadrados perfectos, pues x² = (x)² y 36 = 6². Usando la fórmula:
(x – 6)(x + 6)

Ejemplo 2: Con coeficientes y variables

Factoriza:
9y² – 49

Solución:
Identificamos 9y² = (3y)² y 49 = 7², así que:
(3y – 7)(3y + 7)

Ejemplo 3: Expresiones algebraicas complejas

Factoriza:
4a⁴ – 25b²

Este parece complicado, pero piensa en 4a⁴ = (2a²)² y 25b² = (5b)²:
(2a² – 5b)(2a² + 5b)

Ejemplo 4: Diferencia que no es un cuadrado perfecto

¿Qué pasa con:
x² – 8

Aquí, 8 no es un cuadrado perfecto, por lo que no aplicamos directamente la fórmula.

Más allá de la fórmula: Aplicaciones prácticas de la diferencia de cuadrados perfectos

Durante años enseñando álgebra, he visto cómo dominar esta fórmula ayuda en más áreas de lo que parece:

• Simplificación de fracciones algebraicas: Cuando tienes sumas o restas que integran cuadrados perfectos, factorizar puede simplificar expresiones complejas.
• Resolución rápida de ecuaciones cuadráticas: Al factorizar puede evitar cálculos más extensos de factorización tradicional.
• Cálculos en geometría y física: Algunas fórmulas y problemas aplican identidades algebraicas que incluyen la diferencia de cuadrados.
• Bases para otras técnicas algebraicas: Como la factorización por trinomios o la resolución de polinomios de segundo grado.

Consejos prácticos para que no te quedes atascado con la diferencia de cuadrados perfectos

Durante mi trabajo con estudiantes, estos trucos han sido clave:

• Revisa siempre la posibilidad de simplificar expresiones antes de aplicar la fórmula: A veces, un factor común puede simplificar los términos a cuadrados perfectos.
• Recuerda que la fórmula solo aplica para restas, no sumas. Sin embargo, puedes usar técnicas similares para sumas de cuadrados complejos, pero no con esta fórmula.
• Practica con ejercicios variados: Mientras más practiques, mejor identificarás estas estructuras en problemas reales.
• Utiliza recursos visuales: Diagramas y gráficos pueden ayudarte a entender mejor el concepto del «cuadrado» y su diferencia.

Experiencia personal: Cómo la diferencia de cuadrados perfectos facilitó mi enseñanza

Recuerdo que en una clase de secundaria, varios estudiantes tenían dificultades con factorizaciones, hasta que les enseñé esta fórmula con ejemplos muy prácticos. Muchos lograron mejorar sus notas en solo una semana. Les mostré cómo reconocer rápidamente patrones en expresiones algebraicas y cómo esta herramienta podía evitar horas de cálculos largos.

Esta experiencia me reafirmó lo valioso que es dar ejemplos claros, paso a paso, y acompañar siempre con ejercicios ajustados al nivel real del estudiante.

En resumen: Domina la diferencia de cuadrados perfectos y acelera tu aprendizaje en álgebra

Saber identificar y factorizar la diferencia de cuadrados perfectos es una habilidad que potenciará tu comprensión del álgebra y hará que resolver problemas sea más sencillo y rápido.

Recuerda siempre:

• Identificar los cuadrados perfectos
• Comprobar que los términos estén restados
• Aplicar la fórmula a² – b² = (a – b)(a + b) con confianza

Si sigues estos pasos y practicas con ejemplos variados, dominarás esta técnica en poco tiempo.

Recursos adicionales para profundizar

Para ampliar tus conocimientos y practicar con ejercicios interactivos, te recomiendo visitar Khan Academy, que es una fuente confiable y clara, ideal para estudiantes de todos los niveles.

Además, si quieres llevar tus habilidades en programación y matemáticas al siguiente nivel, visita la plataforma de KeepCoding, donde encontrarás los mejores bootcamps y cursos diseñados para transformar tu carrera tecnológica.