La distribución binominal en estadística Big Data es una de las funciones aplicadas para intentar entender las variables de los datos y su relación entre ellas. Las estadísticas te ayudan a comprender cómo es tu población de los datos. Para ello, esta cuenta con ciertos elementos, como son los estimadores, los percentiles, la varianza, la moda, las operaciones, los tests estadísticos, las asignaciones…
Dentro de estas alternativas se encuentran las distribuciones, que forman parte de las funciones de probabilidad conocidas, es decir, las que aparecen con mayor frecuencia cuando se realiza algún tipo de estudio estadístico. Ahora bien, las distribuciones en estadística Big Data se encuentran en dos grandes grupos: distribuciones continuas y discretas.
La distribución binominal en estadística Big Data forma parte de las distribuciones discretas y es una de las más conocidas y utilizada por lo concisos que son sus resultados. Por ello, en este post, te explicamos en qué consiste la distribución binominal.
Distribución binominal en estadística Big Data
La distribución binomial en estadística Big Data es una generalización de la distribución de Bernoulli para sucesos independientes, cada uno de los cuales tiene dos posibles resultados Sí/No con probabilidad.
Por ejemplo: tirar al aire tres monedas y mirar cuál es la probabilidad de que en dos salga cara.
Variables que definen la distribución:
- p – probabilidad de éxito de un caso individual.
- n – número de los eventos totales que se desean medir.
- k – número de los eventos en los que ha salido SÍ.
Estimadores media y varianza:
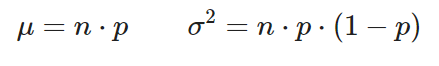
Combinatoria
Para entender cómo se comporta una distribución binominal en estadística Big Data, primero hay que entender un poco cómo funciona la combinatoria.
Puedes saber el número de formas diferentes que hay de obtener, sin tener en cuenta el orden, los objetos que pueden elegirse dentro de un conjunto de k objetos. Es decir, el número de subconjuntos de k-elementos que se pueden obtener de un conjunto de n elementos.
Por ejemplo: si tienes 3 monedas diferentes, ¿cuántas formas posibles hay de agruparlas en grupos de dos?
| . | . | . |
|---|---|---|
| Moneda 2 | Moneda 3 | |
| Moneda 1 | . | Moneda 3 |
| Moneda 1 | Moneda 2 |
El resultado es 3: hay 3 formas posibles de combinar 3 monedas diferentes en grupos de 2.
Este cálculo se puede realizar con el coeficiente binomial:
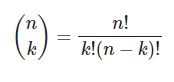
Para este ejemplo de distribución binominal en estadística Big Data:
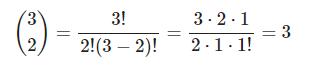
Función de densidad de probabilidad
Si tienes n sucesos independientes que siguen una distribución de Bernoulli, ¿cuál es la probabilidad de que k sucesos sean positivos?
Si sabes que la probabilidad de un suceso (k = 1) que sigue una distribución Bernoulli viene dada por la función de distribución:
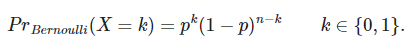
Al tener k sucesos donde.
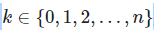
La función será la de Bernoulli multiplicada por el coeficiente binomial que acabas de ver:
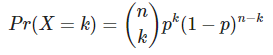
La función acumulativa será:
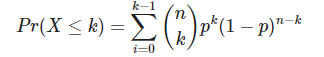
A medida que n se acerca a ∞ y se acerca a 0, la función de probabilidad de una binomial se acerca a una distribución de Poisson con media λ = n · p.
Ejemplo con monedas
Si tiras 3 monedas (no trucadas) al aire, ¿cuál es la probabilidad de que salgan dos caras?
Para este ejemplo, los posibles resultados se muestran en la siguiente tabla:
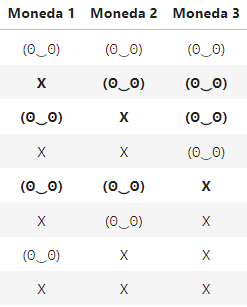
Al ser la probabilidad de cara igual a la probabilidad de cruz, todos los resultados son equiprobables. De los 8 resultados posibles, solo 3 serían válidos, así que la probabilidad es 3/8 = 0.375.
Lo resuelves con la fórmula de la binomial donde n =3, k = 2 y p = 0.5:
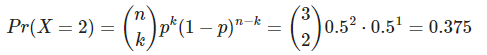
Esto mismo se puede calcular en R con la función dbinom():
dbinom(x=2,size=3,prob=0.5)
0.375
También podrás generar una secuencia de números aleatorios siguiendo una distribución binomial con la función rbinom(). Con la siguiente línea simulamos que ocurre el número de caras que salen al repetir el experimento de las 3 monedas 10 veces.
rbinom(10,size=3,prob=0.5)
- 2
- 3
- 1
- 1
- 1
- 3
- 1
- 0
- 0
- 3
Aprende más sobre el Big Data
Por medio de este post, te hemos expuesto cómo funciona la distribución binominal en estadística Big Data para el desarrollo de cálculos de probabilidad; no obstante, recuerda que puedes contar con otro tipo de distribuciones según la necesidad de tu estudio de los macrodatos. Como buen data scientist, debes conocer todas las alternativas para escoger la mejor solución.
Para facilitarte el proceso de aprendizaje, desde KeepCoding te brindamos el Bootcamp Big Data, con el que te formarás en el proceso de ingesta, clasificación, resguardo, procesamiento y presentación de los macrodatos gracias al uso de diferentes herramientas, sistemas y lenguajes. Terminarás en solo nueve meses y serás capaz de reconocer las ventajas e inconvenientes de los distintos programas estudiados. ¡Mira nuestro temario e inscríbete!







