Distribución conjunta en estadística Big Data

La Distribución conjunta en estadística Big Data es uno de los estadísticos de probabilidad dispuestos entre dos eventos. Su importancia, precisamente, se encuentra en que las variables sean analizadas de manera conjunta, por lo que sus resultados arrojados se presentan como un cuadro comparativo entre diferentes variables.

Por esta razón, en el desarrollo de este post, te compartimos todo lo relacionado con la distribución conjunta en estadística Big Data desde sus variables discretas hasta las continuas, con el fin de que puedas implementar este tipo de cálculo en tu estudio estadístico.

Distribución conjunta en estadística Big Data

La distribución conjunta en estadística Big Data consiste en tener en cuenta dos variables A y B, que se refiere a la distribución de probabilidad de la intersección de ambos eventos.

Por otra parte, la distribución conjunta en estadística Big Data se representa como P(B,A) o P(B ∩ A).

Variables discretas

Para ejemplificar cómo funciona la distribución conjunta en estadística Big Data a partir de dos variables discretas, te presentamos un ejemplo mediante datos inventados.

Imagina que tienes una tabla de contingencia que presenta el número de personas a las que les gusta Star Trek o Star Wars en función del sexo:

tbl<-as.table(matrix(c(122,58,214,120),dimnames = list(c("Star Trek","Star Wars"),c("Mujeres","Hombres")),nrow=2))
tbl

Probabilidad marginal

En esta población, ¿cuál es la probabilidad de que a alguien le guste Star Wars?

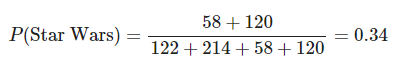
print("La probabilidad de que a alguien le gusta Star Trek o Star Wars es:")
rowSums(tbl)/sum(tbl)

[1] «La probabilidad de que a alguien le gusta Star Trek o Star Wars es:»

Probabilidad conjunta

¿Cuál es la probabilidad de que una persona elegida al azar sea hombre y le guste Star Wars?

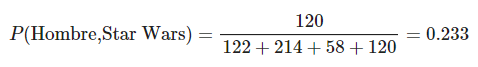
print("La matriz de la probabilidad conjunta es:")
prop.table(tbl

[1] «La matriz de la probabilidad conjunta es:»

Probabilidad condicional

Suponiendo que te fijas solamente en los hombres, ¿cuál es la probabilidad de que Star Wars sea la película más interesante?

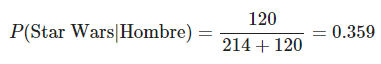
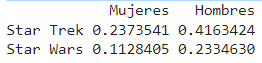
print("La matriz condicional para mujeres y hombres:")
prop.table(tbl,margin = 2)

[1] «La matriz condicional para mujeres y hombres:»

Ahora, suponiendo que te fijas solamente en los fans de Star Wars, ¿cuál es la probabilidad de que el fan sea hombre?

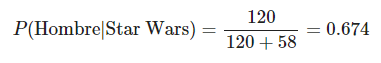
print("La matriz condicional para Star Trek y Star Wars :")
prop.table(tbl,margin = 1)

[1] «La matriz condicional para Star Trek y Star Wars :»

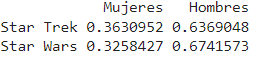
Propiedades

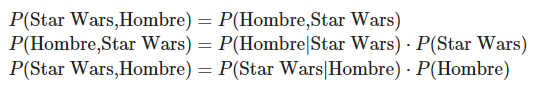
Variables continuas

Ahora, con el fin de mostrar cómo funciona la distribución conjunta en estadística Big Data con variables continuas, también te exponemos datos aleatorios.

Dos variables independientes

En este caso: P(B,A)=P(B)·P(A).

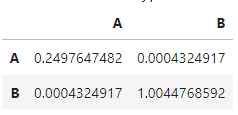
Es fácil verlo, porque su matriz de covarianza se parece a una matriz diagonal.

N<-10000
A<-rnorm(N,mean=0,sd=0.5)
B<-rnorm(N,mean=0,sd=1)
df<-data.frame(A,B)

print(paste("Matriz de covarianza:"))
cov(df)

library(ggplot2)
ggplot(df, aes(x=A, y=B))+geom_density2d(aes(colour=..level..)) + 
  stat_density2d(aes(fill=..level..,alpha=..level..),geom='polygon',colour='black') + 
  scale_fill_continuous(low="green",high="red") +    
  geom_point(alpha=0.2,size=0.1)+
  theme_bw()+theme(legend.position="none")+xlim(c(-5,5))+ylim(c(-5,5))

[1] «Matriz de covarianza:»
A matrix: 2 × 2 of type dbl

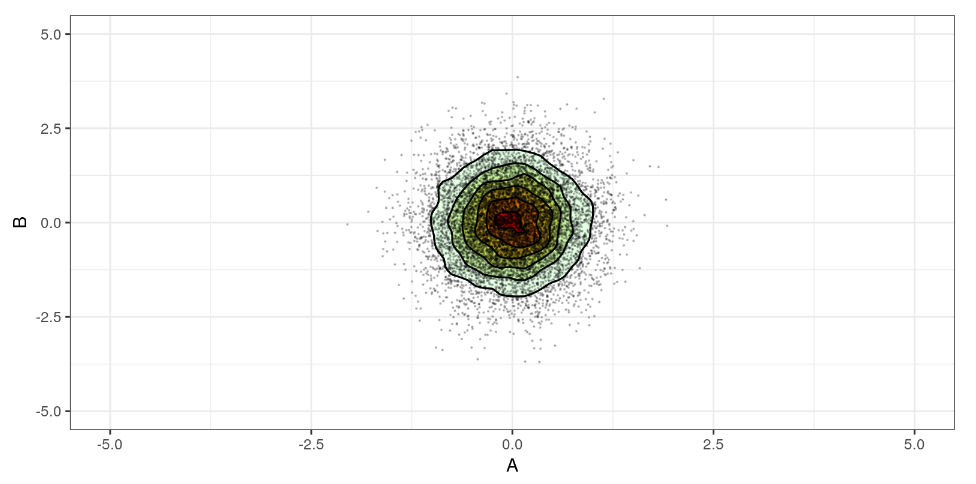
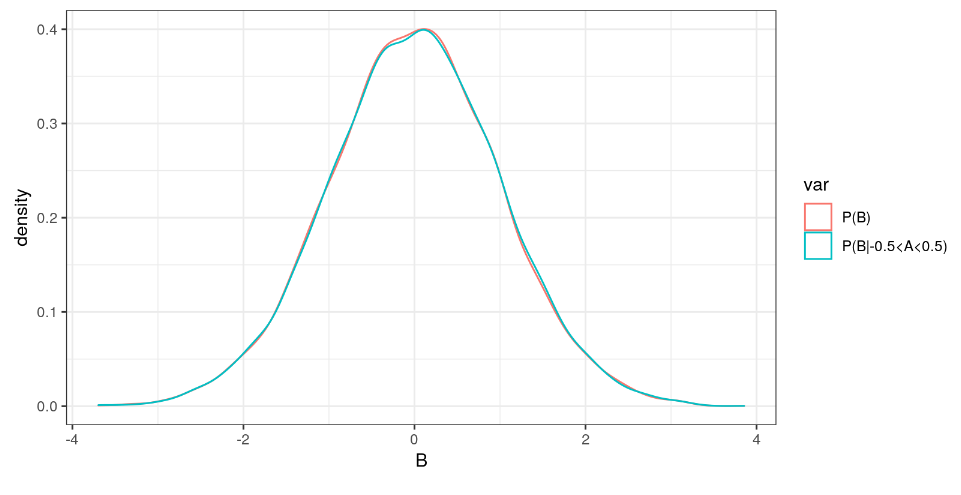
Como son independientes, la probabilidad condicional de B respecto a A es igual a la probabilidad de B.

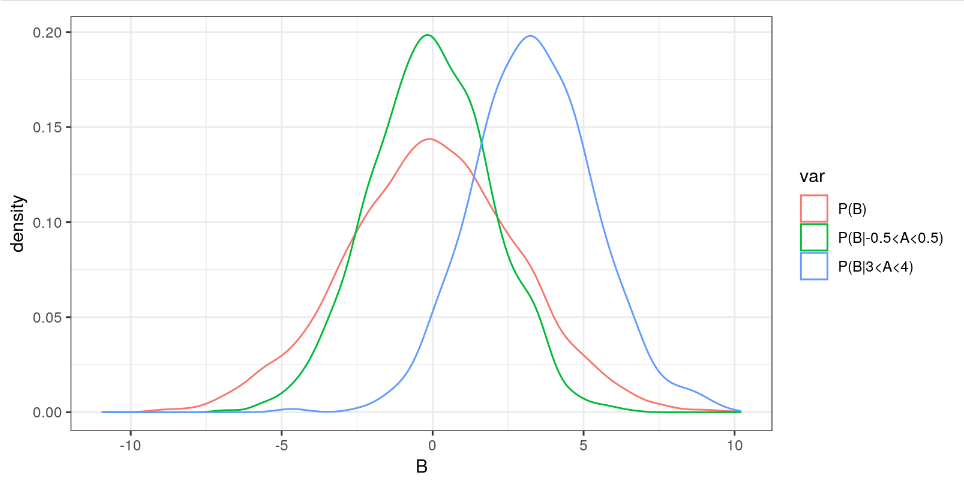
P(B|A)=P(B)

dfPartialProbs<-data.frame(B=B,var="P(B)")
dfPartialProbs<-rbind(dfPartialProbs,data.frame(B=df$B[df$A>-0.5 & df$A<0.5],var="P(B|-0.5<A<0.5)"))


ggplot(dfPartialProbs, aes(x=B,color=var))+geom_density()+
  theme_bw()

Dos variables dependientes

En este caso de la distribución conjunta en estadística Big Data con dos variables dependientes: P(B,A)=P(B|A)·P(A)=P(A,B)=P(A|B)·P(B).

Así, la matriz de covarianza no es diagonal.

N<-10000
A<-rnorm(N,mean=0,sd=2)
B<-A+rnorm(N,mean=0,sd=2)
df<-data.frame(A,B)

print(paste("Matriz de covarianza:"))
cov(df)

library(ggplot2)
ggplot(df, aes(x=A, y=B))+geom_density2d(aes(colour=..level..)) + 
  stat_density2d(aes(fill=..level..,alpha=..level..),geom='polygon',colour='black') + 
  scale_fill_continuous(low="green",high="red") +    
  geom_point(alpha=0.1,size=0.1)+
  theme_bw()+theme(legend.position="none")+xlim(c(-10,10))+ylim(c(-10,10))

[1] «Matriz de covarianza:»
A matrix: 2 × 2 of type dbl

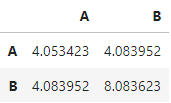
Warning message:
“Removed 4 rows containing non-finite values (stat_density2d).”
Warning message:
“Removed 4 rows containing non-finite values (stat_density2d).”
Warning message:
“Removed 4 rows containing missing values (geom_point).”

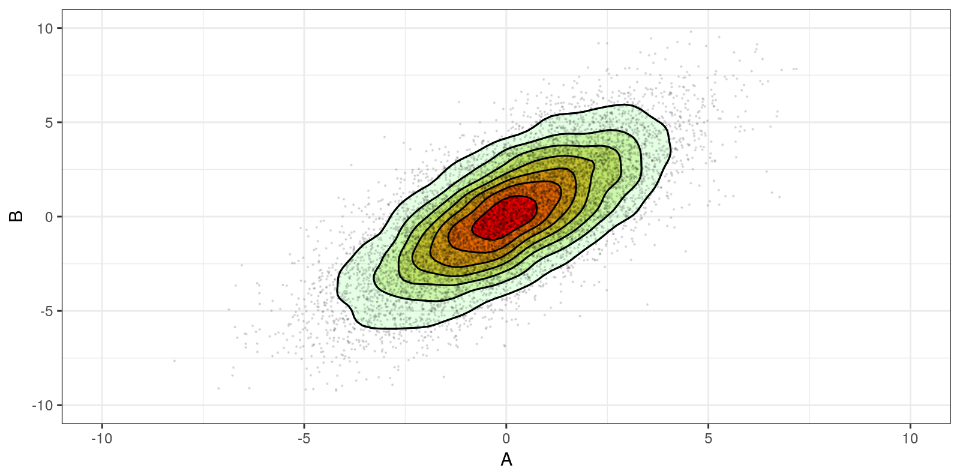
Como son dependientes, la probabilidad condicional de B respecto a A es diferente a la probabilidad de B.

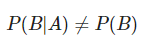
dfPartialProbs<-data.frame(B=B,var="P(B)")
dfPartialProbs<-rbind(dfPartialProbs,data.frame(B=df$B[df$A>-0.5 & df$A<0.5],var="P(B|-0.5<A<0.5)"))

dfPartialProbs<-rbind(dfPartialProbs,data.frame(B=df$B[df$A>3 & df$A<4],var="P(B|3<A<4)"))


ggplot(dfPartialProbs, aes(x=B,color=var))+geom_density()+
  theme_bw()

Sigue aprendiendo sobre el Big Data

En el desarrollo de este post te hemos familiarizado con todo lo relacionado con lo que es la distribución conjunta en estadística Big Data, sin embargo, a pesar del conocimiento teórico y de los ejemplos prácticos, este tipo de saber exige mucha precisión, por lo que conlleva práctica y tiempo. En suma, todavía quedan muchos más temas por abordar con respecto al manejo de los macrodatos, ¡así que debe seguir aprendiendo sobre el Big Data!

Desde KeepCoding te presentamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Por medio del mismo, podrás aprender más sobre la suite de Talend Open Studio junto a las demás herramientas Big Data a través de diferentes módulos, como el de Big Data Architecture. Además, podrás instruirte tanto de manera teórica como práctica. ¡No esperes más y apúntate ya!