La distribución gaussiana en estadística Big Data hace referencia a un tipo de cálculo de probabilidad muy utilizado en el desarrollo de un estudio estadístico para el manejo de los macrodatos. Por esta razón, conocer cómo funciona en este tipo de distribución es de suma importancia antes de comenzar con este tipo de análisis.
En efecto, pensar en estas estrategias de facilitación te ayudará a llevar a cabo un procesamiento de los datos mucho más efectivo, puesto que conocerás a fondo qué tipo de información puedes sacar y valorar de la información. Por este motivo, en este post, te hablamos sobre la distribución gaussiana en estadística Big Data.
Distribución gaussiana en estadística Big Data
La distribución gaussiana en estadística Big Data es, posiblemente, la distribución de probabilidad más utilizada, precisamente, porque es la distribución básica para un análisis estadístico. También se conoce como distribución normal. La importancia de esta distribución, además, radica en que cuenta con el teorema central del límite.
Por otra parte, la función de densidad de probabilidad es:
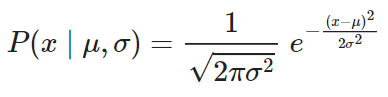
Mientras que la función acumulativa de probabilidad no tiene una forma explícita:
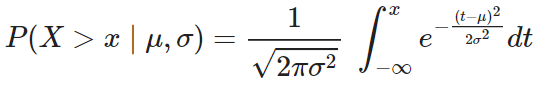
El teorema central del límite establece que, para distribuciones independientes e idénticamente distribuidas con media y varianza, la suma de un gran número de variables aleatorias se distribuye aproximadamente como una normal.

Regla 68-95-99.7
Es una regla para acordarse de la distribución de datos cuando estos siguen una distribución gaussiana. Te dice qué porcentaje de datos se encuentran separados de la media en una, dos o tres desviaciones típicas. Es similar a la desigualdad de Tschebyshev, pero más restrictiva, ya que solo es válida para distribuciones gaussianas.
Histograma variable gaussiana:
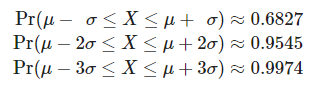
Funciones en R
En R, para la distribución gaussiana en estadística Big Data contarás con las siguientes funciones:
- dnorm(x, mean = 0, sd = 1): da la probabilidad de P(X=x).
- pnorm(q, mean = 0, sd = 1): da la probabilidad acumulada de P(X<x).
- qnorm(p, mean = 0, sd = 1): devuelve resultados de los percentiles (cuantiles),es decir, da el valor de x tal que P(X<x)=p.
- rnorm(n, mean = 0, sd = 1): genera un vector aleatorio de dimensión n.
Donde la media y la desviación típica se definen con los parámetros mean y sd y la función qnorm es la inversa de pnorm.
pnorm(200,mean=170,sd=20)
0.933192798731142
x<-seq(-5,5,length.out=100)
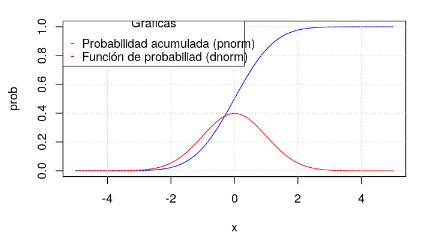
plot(x,pnorm(x),t="l",col="blue",ylab="prob")
lines(x,dnorm(x),t="l",col="red")
#lines(qnorm(x),x,t="l",col="green")
grid()
legend("topleft", c("Probabilidad acumulada (pnorm)","Función de probabiliad (dnorm)"),
pch = '-', title = "Gráficas", col=c("blue","red"), y.intersp = 2)
Efecto de la variación media y varianza
El gráfico elaborado por el IPCC en 2001, hace casi dos décadas, en el que ya se describía cómo aumentaría la frecuencia de olas de calor al aumentar la temperatura media. Muestra el efecto en temperaturas extremas cuando (a) aumenta la temperatura media, (b) aumenta la varianza y (c) cuando la media y la varianza aumentan para una distribución normal de la temperatura.
Operaciones con gaussianas
Sumar una constante a una variable aleatoria gaussiana modifica su media en la misma medida. Mientras, multiplicarle una constante a una variable aleatoria gaussiana cambia su media y desviación típica por el mismo factor.
x<-rnorm(100000, mean = 4, sd = 2)
print(paste0("Tenemos una variable aleatoria gausiana de media: ",
mean(x)," y desviación típica:",sd(x)))
[1] “Tienes una variable aleatoria gausiana de media: 3.99909165392521 y desviación típica: 1.99854987357272”
nm<-6
x<-x+nm
print(paste0("Si le sumamos ",nm," su nueva media será: ",mean(x)," y desviación típica:",sd(x)))
[1] “Si le sumas 6 su nueva media será: 9.99909165392521 y desviación típica: 1.99854987357272”
nsd<-1.5
x<-x*nsd
print(paste0("Si la multiplicamos por ",nsd,
" su nueva media será: ",mean(x)," y desviación típica:",sd(x)))
[1] “Si la multiplicas por 1.5 su nueva media será: 14.9986374808878 y desviación típica: 2.99782481035909”
Aprende muchos más del Big Data
En este post, te hemos expuesto cómo funciona la distribución gaussiana en estadística Big Data para que puedas implementarla en tu procesamiento de los macrodatos. Sin embargo, debes tener en cuenta que también podrías necesitar de otro tipo de distribución, por lo que te aconsejamos conocer mucho más sobre todas estas alternativas.
Por ello, en KeepCoding te recomendamos participar en el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning para continuar con tu formación. En esta formación, se te presentarán los fundamentos del aprendizaje automático, con énfasis en algoritmos de clasificación y regresión. Al finalizar este módulo, serás capaz de conocer las ventajas e inconvenientes de los distintos algoritmos analizados y de aplicar buenas prácticas en el entrenamiento de modelos de aprendizaje automático. ¡No esperes más, pide información y empieza ahora!







