Distribución uniforme en estadística Big Data

La distribución uniforme en estadística Big Data forma parte de las estrategias y dinámicas para que se lleven a cabo los procesos de probabilidad en un estudio estadístico de los macrodatos. De la mano de esta distribución, también podrás contar con la distribución gaussiana, chi-cuadrado, Bernoulli, binomial, Poisson o exponencial, entre varias otras.

Para elegir la distribución que mejor funcione con tu procesamiento de los datos, resulta necesarios que conozcas cada una de estas y sus funciones de probabilidad. De esta manera, te asegurarás de que los resultados arrojados sean mucho más efectivos y, por tanto, también las decisiones derivadas de ellos.

Por este motivo, en este post, te explicamos a qué hace referencia la distribución uniforme en estadística Big Data para que puedas emplearla en tus estudios data.

Distribución uniforme en estadística Big Data

La distribución uniforme en estadística Big Data es una familia de funciones de probabilidad donde cada uno de los elementos que se encuentran dentro de cierto intervalo tienen la misma probabilidad de aparecer.

Por ejemplo: en la lotería, todos los números tienen las mismas posibilidades, lo que se ilustraría así:

Por otra parte, la distribución uniforme en estadística Big Data cuenta con las siguientes fórmulas para los estimadores de la media y la varianza:

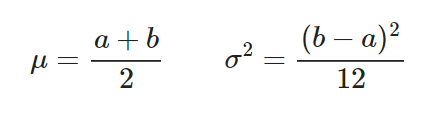
En cuanto a las funciones en el lenguaje de programación R, contarás con:

• runif(x,min=a,max=b): genera x números aleatorios.
• dunif(x,min=a,max=b): función de densidad en el punto x (likelihood).
• punif(x,min=a,max=b): probabilidad acumulada P(X<x)=p.
• qunif(p,min=a,max=b): inversa de la probabilidad acumulada P(X<x)=p.

Por último, podrás generar una variable aleatoria que siga una distribución uniforme mediante la función runif().

Ejemplo práctico

Ahora, te compartimos un ejemplo práctico que te muestra cómo funciona la distribución uniforme en estadística Big Data.

Para generar 10.000 muestras de una distribución uniforme entre 2 y 7, basta con ejecutar:

# set.seed(1)
myUnifVector<-runif(10000,min=2,max=7)
summary(myUnifVector)
length(myUnifVector)

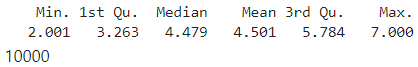
dunif(5,min=2,max=7)

0.2

punif(4.5, min=2, max=7)

0.5

qunif(0.15, min=2, max=7)

2.75

En esta distribución uniforme en estadística Big Data, podrás ver cómo el histograma de myUnifVector se parece bastante a la función de densidad de probabilidad esperada:

library(ggplot2)

ggplot(data=data.frame(x=myUnifVector), aes(x))+
  geom_histogram(bins=15,fill="#7070BB",color="#010101")+ 
  scale_x_continuous(breaks = seq(0,10,1), lim=c(0,10))

Warning message:
“Removed 2 rows containing missing values (geom_bar).”

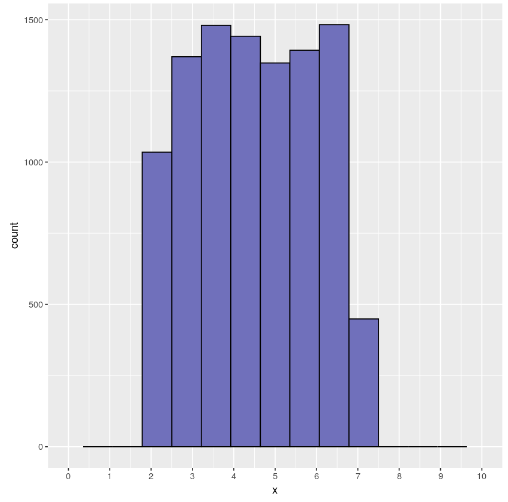
Las barras que se encuentran en los límites de la distribución, en 2 y 7, aparecen más bajas porque realmente tienen menos elementos. Parte de la barra cae fuera de los límites de la distribución uniforme.

Esto se puede solucionar haciendo las barras más finas, añadiendo más barras a costa de empeorar la precisión.

ggplot(data=data.frame(x=myUnifVector), aes(x))+
  geom_histogram(bins=50,fill="#7070BB",color="#010101")+ 
  scale_x_continuous(breaks = seq(0,10,1), lim=c(0,10))

Warning message:
“Removed 2 rows containing missing values (geom_bar).”

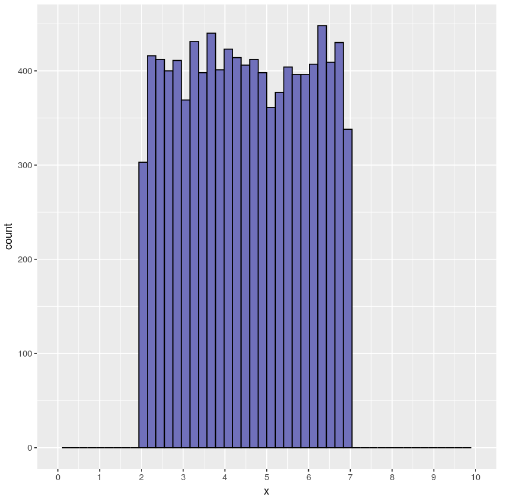
Cuantas más barras utilicemos, más resolución tendremos, pero demasiadas te pueden alejar de la función de densidad de probabilidad real.

Si tienes pocas muestras, el histograma aparecerá con muchas variaciones, por lo que puede ser difícil intuir la función de densidad de probabilidad.

Lo ideal sería utilizar unas barras muy estrechas para calcular el histograma y luego suavizar la función resultante para evitar los saltos bruscos. Si posteriormente normalizas por el número de muestras, acabas con una estimación de la función de densidad de probabilidad.

También debes considerar que la librería ggplot incorpora la función geom_density() que hace eso mismo: estima la función de densidad de probabilidad utilizando diferentes funciones de suavizado.

ggplot(data=data.frame(x=myUnifVector), aes(x))+
  geom_density(fill="#7070BB",color="#010101")+ 
  scale_x_continuous(breaks = seq(0,10,1), lim=c(0,10))

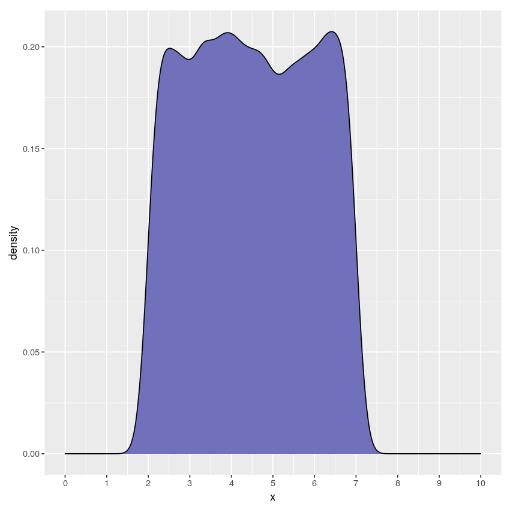
Por la función de suavizado (llamada kernel) es una gaussiana, pero en este caso particular encajaría mejor una función rectangular, que tiene una caída más abrupta.

ggplot(data=data.frame(x=myUnifVector), aes(x))+
  geom_density(fill="#7070BB",color="#010101",kernel="rectangular", bw=0.07)+ 
  scale_x_continuous(breaks = seq(0,10,1), lim=c(0,10))

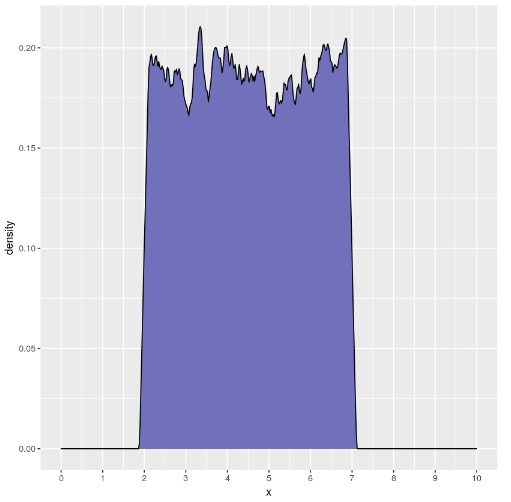
ggplot(data=data.frame(x=myUnifVector), aes(x))+
  geom_density(fill="#7070BB",color="#010101",kernel="rectangular", bw=0.01)+ 
  scale_x_continuous(breaks = seq(0,10,1), lim=c(0,10))

¿Cómo aprender más del Big Data?

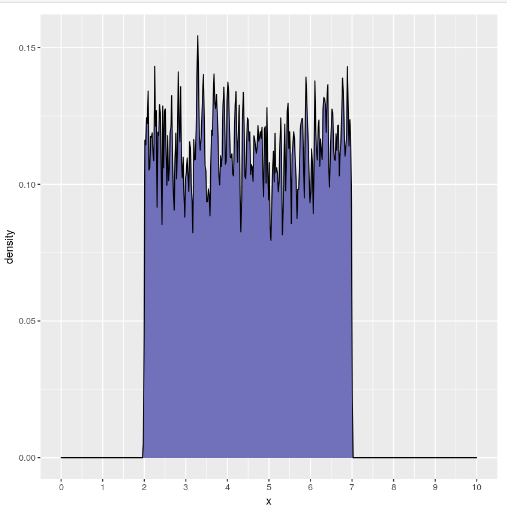
En el desarrollo de este post, te hemos explicado qué es la distribución uniforme en estadística Big Data. Ahora debes poner en consideración todas las demás distribuciones con las que podrás contar para llevar a cabo un estudio estadístico. ¿Quieres aprender más sobre el manejo del Big Data?

Para facilitarte el proceso de aprendizaje, desde KeepCoding te brindamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, por medio del que te formarás en el proceso de ingesta, clasificación, resguardo, procesamiento y presentación de los macrodatos gracias al uso de diferentes herramientas, sistemas y lenguajes. Al finalizar, en menos de nueve meses, serás capaz de reconocer las ventajas e inconvenientes de los distintos programas estudiados. ¡Echa un vistazo a nuestro temario e inscríbete ahora!