En este artículo desarrollaremos un ejercicio de aplicación en R sobre regresión lineal con T Distribution y ANOVA, que consiste en evaluar la efectividad de una dieta.
Ejercicio de aplicación en R
En este ejercicio de aplicación en R, los datos contienen información de 76 personas que tomaron una de las tres dietas (1, 2 o 3). Además, se aporta información extra como edad, género y altura. El objetivo del estudio y del ejercicio de aplicación en R es comparar cuál de las tres dietas es la mejor para perder peso.
In [29]: diet = read.csv("data/stcp-Rdataset-Diet.csv", row.names=1)
head(diet)
diet$loss<-diet$pre.weight - diet$weight6weeks
dietsDiet<-factor(dietsDiet)
diet$gender<-factor(dietsgender, labels=c("female", "male"))
str(diet)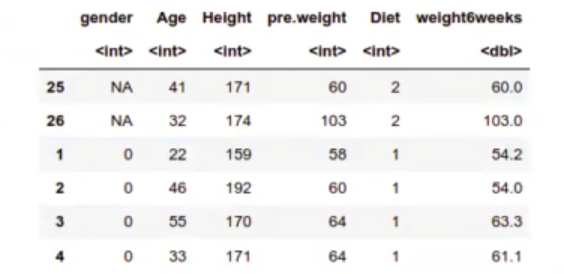
‘data.frame’: 78 obs. of 7 variables:
$ gender : Factor w/ 2 levels «female», «male»: NA NA 1 1 1 1 1 1 1 1 …
$ Age: int 41 32 22 46 55 33 50 50 37 28 …
$ Height : int 171 174 159 192 170 171 170 201 174 176 …
$ pre.weight: int 60 103 58 60 64 645 66 67 69 …
$ Diet: Factor w/ 3 levels «1»,»2″,»3″: 2 2 1 1 1 1 1 1 1 1 …
$ weight6weeks: num 60 103 54.2 54 63.3 61.1 62.2 64 65 60.5 …
$ loss: num 0 0 3.86 0.7…
Hacemos un ggplot del ejercicio de aplicación en R relacionado con la pérdida de peso:
In [30]: options (repr.plot.height=4, repr.plot.width=6, repr.plot.res=200)
ggplot (diet, aes(y=loss, x=Diet, color=Diet))+geom_boxplot()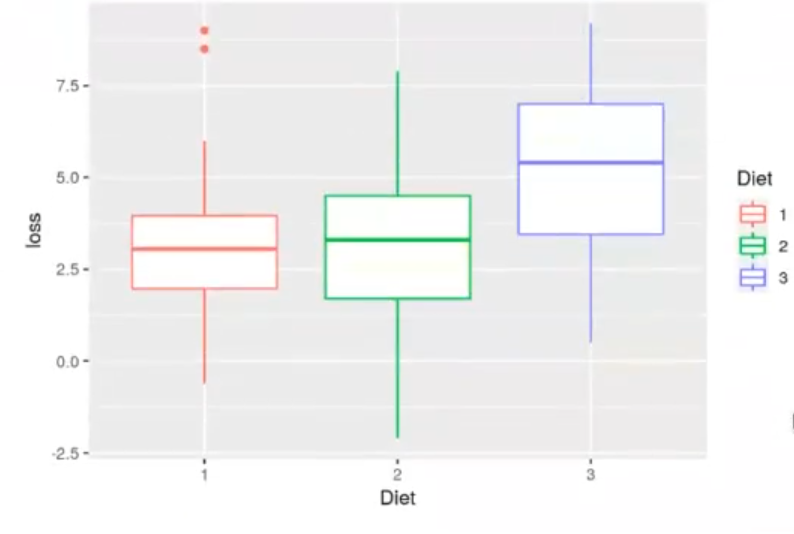
Al parecer, las dietas uno y dos tienen más peso que la tres.
Ahora, trataremos de confirmar esto con la regresión lineal:
In [33]: model<-lm(data=diet, formula=loss~ Diet)
summary (model)Call:
lm(formula=loss~Diet, data=diet)
Residuals:
Min: -5.1259
1Q: -1.3815
Median: 0.1759
3Q: 1.6519
Max: 5.7000
Coefficients:
| Estimate | Std. Error | t value | Pr(>ltl) | |
| (Intercept) | 3.3000 | 0.4889 | 6.750 | 2.72e-09 *** |
| Diet2 | -0.2741 | 0.6719 | -0.408 | 0.68449 |
| Diet3 | 1.8481 | 0.6719 | 2.751 | 0.00745 ** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘ . ‘ 0.1 ‘ ‘ 1
Residual standard error: 2.395 on 75 degrees of freedom
Multiple R-squared: 0.1418
Adjusted R-squared: 0.1189
F-statistic: 6.197 on 2 and 75 DF
p-value: 0.003229
El resultado lo que nos está diciendo es que con la dieta1 se pierden 3 kilos (3.3000) y en la dieta2 se pierden casi los mismos tres kilos (3.3000 -(-0.2741)). El valor t (Pr(>ltl)) es de 0.68 para la dieta2, lo cual indica que no podemos fiarnos de este valor. La dieta1 y la dieta2 son prácticamente las mismas, dados los valores obtenidos.
En cambio, en la dieta3 sí se baja 1.8481 kilos más que la dieta1. Además, tiene un valor t más bajo, lo cual brinda una seguridad respecto a los resultados.
Ahora, mostraremos los resultados del cálculo de la media para la dieta1, dieta2 y dieta3:
In [34]:
diet3<-mean (subset(diet,Diet==3)$loss)
diet2<-mean (subset(diet, Diet==2)$loss)
dietl<-mean (subset diet, Diet==1)$loss)
paste("Perdida de peso por dieta 1: ", diet1, ". Es igual a:", model$coef[1])
paste("Perdida de peso por dieta 2 : ", diet2, ". Es igual a:", model$coef[1]+model$coef [2])
paste("Perdida de peso por dieta 3:, diet3, ". Es igual a:", model$coef[1]+model$coef[3])‘Perdida de peso por dieta 1: 3.3. Es igual a: 3.3″
«Perdida de peso por dieta 2 : 3.02592592592593. Es igual a: 3.02592592592593
‘Perdida de peso por dieta 3: 5.14814814814815. Es igual a: 5.14814814814815
Con este ejercicio de aplicación en R hemos podido confirmar que la dieta 3 es la más efectiva.
Si quieres saber las miles de posibilidades que existen para potenciar este ejercicio, inscríbete a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el cual podrás aprender todo lo relacionado con este mundillo e incursionar en el mercado laboral rápidamente. ¡Pide ahora más información!











