En este post veremos un ejemplo de boosted trees con clasificación. Los boosted trees son, como su nombre indica, árboles modificados de tal manera que permiten hacer las cosas que los árboles individuales no, al tiempo que mejoran los problemas que estos árboles por sí solos no pueden solucionar. De ahí su gran relevancia en el campo del machine learning y la razón por la cual realizaremos un ejemplo de estos boosted trees con clasificación. Para ello, utilizaremos el Pima Indians Diabetes Database.
Boosted trees con clasificación: ejercicio
Lo primero que haremos será cargar las librerías y funciones necesarias:
#Boosted trees con clasificación
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
%matplotlib inline
cm = plt.cm.RdBu
cm_bright = ListedColormap (['#FF0000", "#0000FF"])
import warnings
warnings.filterwarnings ('ignore')Acto seguido, cargaremos los datos:
#Boosted trees con clasificación
data = pd.read_csv ('./data/diabetes.csv')
data.head ()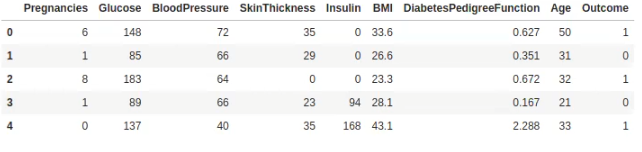
#Boosted trees con clasificación
data ['Outcome'].value.counts ()0 500
1 268
Name: Outcome, dtype: int64
El value counts nos dice que se tienen datos binarios y que, aunque no está balanceado el resultado, tampoco es una locura. Si bien sí está desbalanceado y habrá que tener cuidado, no lo está de una manera exorbitante.
Ahora lo que haremos será representar el histograma de cada variable separado por clases. ¿Hay alguna característica que convenga transformar?
Antes de meternos con los histogramas, vamos a hacer un análisis exploratorio un poco más en profundidad. Haremos un describe para determinar cuántas variables o instancias tenemos. En este caso, el resultado nos arroja que son 768 (count = 768):
#Boosted trees con clasificación
data.describe ()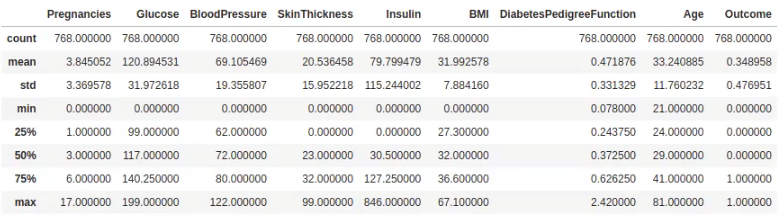
Ahora, realizaremos un data.types para verificar que todas son numéricas, porque aparentemente lo son, pero con este simple comando podremos comprobarlo de manera certera:
data.dtypesPregnancies int64
Glucose int64
BloodPressure int64
SkinThickness int64
Insulin int64
BMI float64
DiabetesPedigreeFunction float64
Age int64
Outcome int64
dtype: object
Efectivamente, todas son numéricas.
Tras esta verificación, realizaremos otra para mirar si hay algún missing o valor faltante.
data.isnull ().any ()Pregnancies False
Glucose False
BloodPressure False
SkinThickness False
Insulin False
BMI False
DiabetesPedigreeFunction False
Age False
Outcome False
dtype: bool
Corroboramos que, en efecto, no existe ningún valor nulo dentro del conjunto de datos que hemos cargado.
#Boosted trees con clasificación
#Pintamos histogramas para cada clase
plt.figure (figsize = (20, 10))
idx = data ['Outcome'] == 0
idx 1 = data['Outcome'] == 1
for i, feature in enumerate (data.columns.drop (['Outcome'])):
plt.subplot (2, 4, i + 1)
plt.hist (data.loc [idx_0, feature], density = 0, alpha = 0.75, label = 'y = 0')
plt.hist (data.loc [idx_1, feature], density = 0, facecolor = "red", alpha = 0.75, label ='y =1')
plt.legend ()
plt.title (feature)
plt.show ()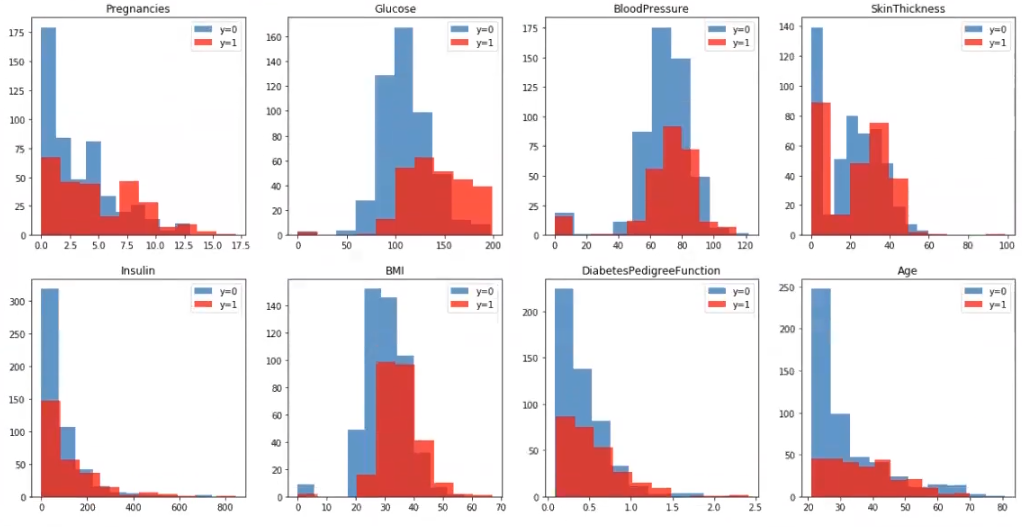
Ahora evaluaremos el dataset para ver si existe algún tipo de correlación entre variables:
#Boosted trees con clasificación
import seaborn as sns
#Compute the correlation matrix
corr = np.abs (data.drop (['Outcome], axis = 1).corr ())
# Generate a mask for the upper triangle
mask= np. zeros_like (corr, dtype = np.bool)
mask [np.triu_indices_from (mask)] = True
#Set up the matplotlib figure
f, ax = plt.subplots (figsize = (12, 10))
#Draw the heatmap with the mask and correct aspect ratio
sns.heatmap (corr, mask = mask, vmin = 0.0, vmax = 1.0, center = 0.5, linewidths = 1, cmap = "YlGnBu", cbar_kws = {"shrink": .8})
plt.show ()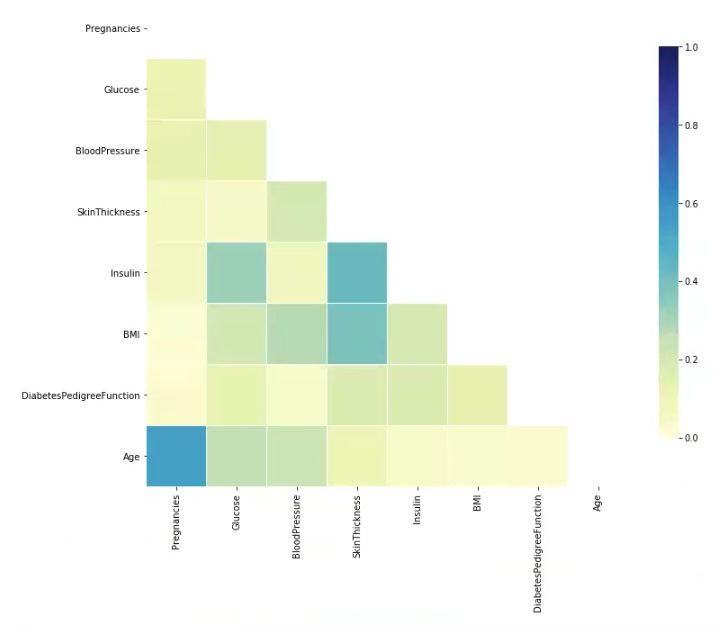
Según este diagrama, apenas existe correlación. La única correlación que existe es entre Age y Pregnancies; esto es entendible, ya que, a mayor edad, mayor número de embarazos.
La correlación más alta, pues, se da entre Age y Pregnancies, ya el resto son correlaciones bastante más bajas.
Teniendo en cuenta este resultado, nosotros no haríamos nada con él, ya que si no existe mucha correlación entre ninguna variable en específico, no existirán problemas de otra índole en algún aspecto.
A la vista de los histogramas anteriores, ¿cómo de separable crees que es el problema? El concepto general es que no parece que sean muy separables. Ambos grupos de histogramas, tanto el 0 como el 1, están muy juntos, superpuestos, con lo cual no va a ser muy separable el problema que se plantea.
Los boosted trees son árboles muy útiles para tratar principalmente problemas de mayor complejidad que los árboles habituales. Si quieres seguir aprendiendo sobre una de las disciplinas más demandadas en la actualidad, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que podrás adquirir todas las herramientas teóricas y prácticas para incursionar en un mundo que está lleno de oportunidades estupendas para ti. ¡Anímate a impulsar tu vida y solicita más información ahora!











