En este artículo veremos un ejemplo de LDA para clases múltiples.
Recordemos que el análisis discriminante lineal o LDA para clases múltiples es el lugar en el que le podemos sacar muchísimo provecho al LDA, ya que la idea es la misma que si tuviéramos una o dos clases, con las que podemos usar la regresión logística: encontrar un plano sobre el que proyectar.
No obstante, dado que son clases múltiples, utilizaremos un ejemplo de LDA para clases múltiples para que veamos cómo funciona este en contexto.
Ejemplo de LDA para clases múltiples
Para este ejemplo utilizaremos el conjunto de datos Iris:
#Ejemplo de LDA para clases múltiples idx <- sample (1 : nrow (iris), nrow (iris) * 0.7) iris_train <- iris [idx , ] iris_test <- iris [ - idx , ] X <- iris_train [ , 1 : 4] X <- as.matrix (X) Cl <- iris_train$Species p <- ncol (X)
table(Cl)

#Ejemplo de LDA para clases múltiples
mu <- colMeans (X)
Sb = matrix (0L, nrow = p, ncol = p)
for (k in levels (Cl)) {
mu_k = colMeans (X [Cl == k, ])
N_k = sum (Cl == k)
Sb = Sb + N_k * (mu_k - mu) %*% t (mu_k - mu)
}
Sb
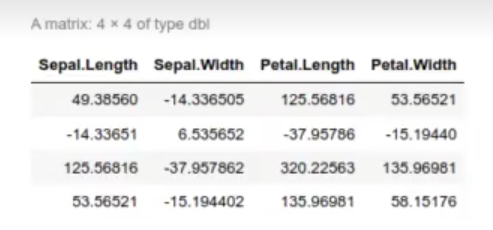
#Ejemplo de LDA para clases múltiples
Sw <- matrix (0L, nrow = p, ncol = p)
for (k in levels (Cl)) {
X_k <- X [Cl == k, ]
mu_k = colMeans (X [Cl == k, ])
for (i in 1 : nrow (X_k)) {
X_i <- as.matrix (X_k [ 1 , ])
Sw <- Sw + (X_i - mu_k) %*% t (X_i - mu_k)
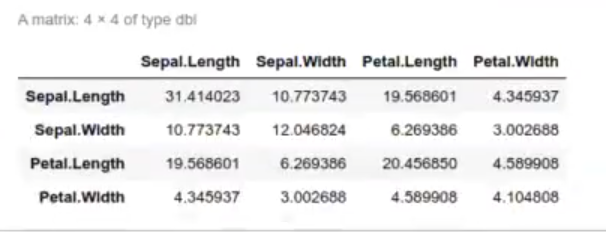
(Solve (Sw) %*% Sb)
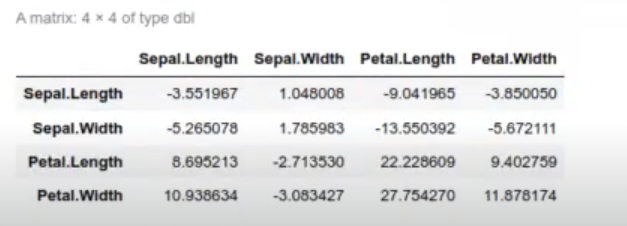
Tenemos las matrices de S y Sw, que son una especie de covarianza.
eig <- eigen (Solve (Sw) %*% Sb) eig
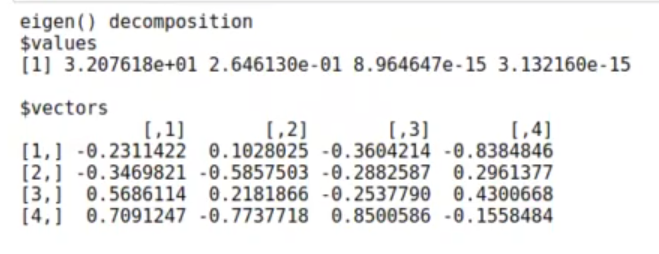
Aquí tenemos los autovectores.
Realmente la proyección óptima debería ser sobre K – 1, es decir, 2 columnas. Con los dos primeros autovectores podríamos definir bien las fronteras entre las 3 clases:
W <- Re (eig$vectors [ , 1 : 2]) W head (X %*% W)
Si multiplicamos nuestro valor X original por w, nos da como resultado esta proyección, que separa al máximo las tres clases:
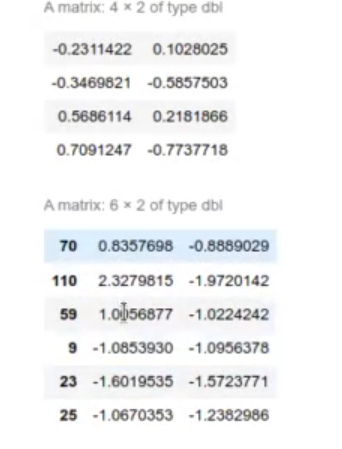
#Ejemplo de LDA para clases múltiples library (MASS) l <- lda (formula = Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, data = iris_train) l
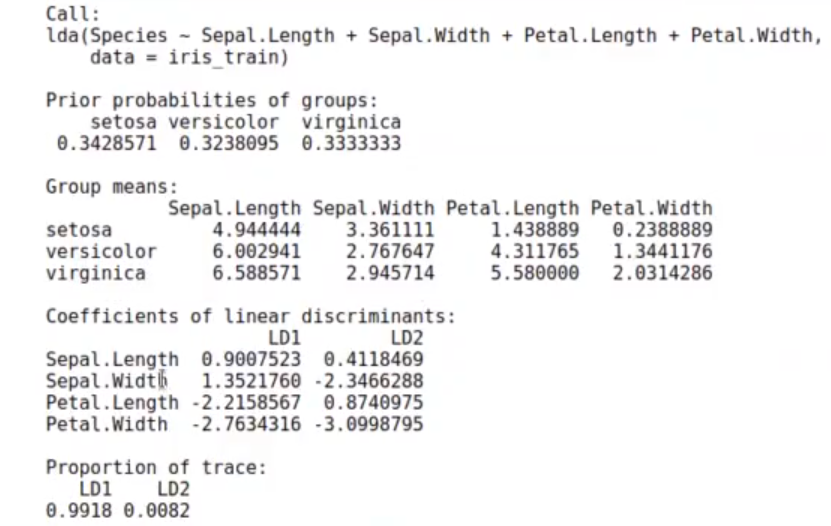
Aquí me da dos discriminantes lineales, que dicen que para conseguir el discriminante lineal tenemos que multiplicar el largo y ancho del sépalo y el pétalo por cada uno de los valores que aparecen en la columna LD1 de la anterior imagen.
W l$scaling / sqrt (colSums (l$scaling ^ 2))
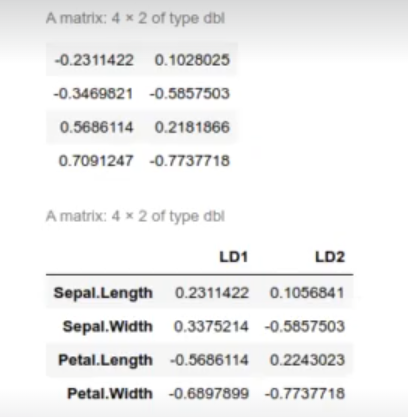
#Ejemplo de LDA para clases múltiples
W <- eig$vectors [ ,1 : 2]
iris_train [ , c ("projX1", "projX2")] <- Re (X *% W)
ggplot (iris_train, aes (x = projX1, y = projX2, color = Species)) + geom_point()
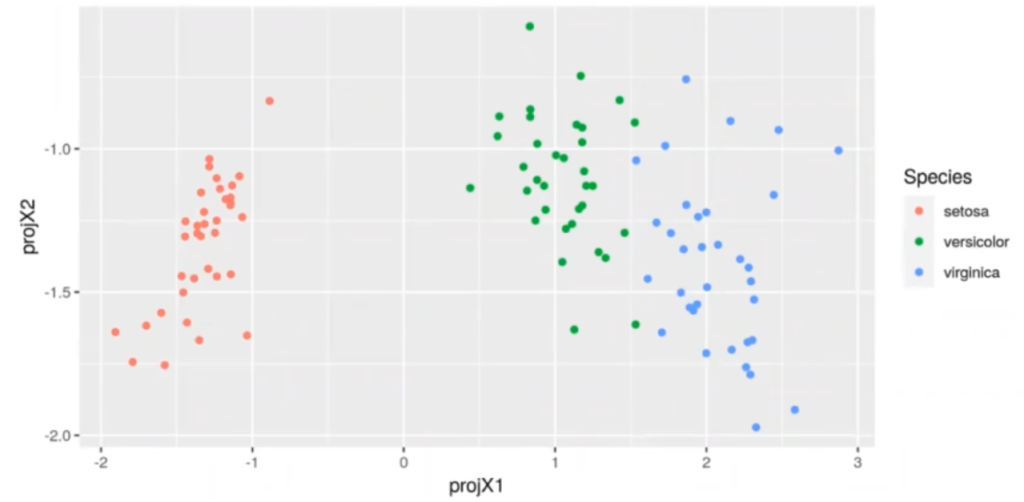
Como vemos, el mayor poder discriminante se encuentra en la primera proyección, que es la que corresponde al autovalor más grande. Esto tiene sentido porque el primer autovector es 100 veces más grande que el segundo. Esto indica que la primera dimensión tiene casi todo el poder discriminante.
Podemos comprobarlo proyectando solo sobre el primer discriminante:
#Ejemplo de LDA para clases múltiples W <- eig$vectors [ , 1] iris_train$projection <- Re (X %*% W) ggplot (iris_train, aes (x = projection.color = Species)) + geom_density)
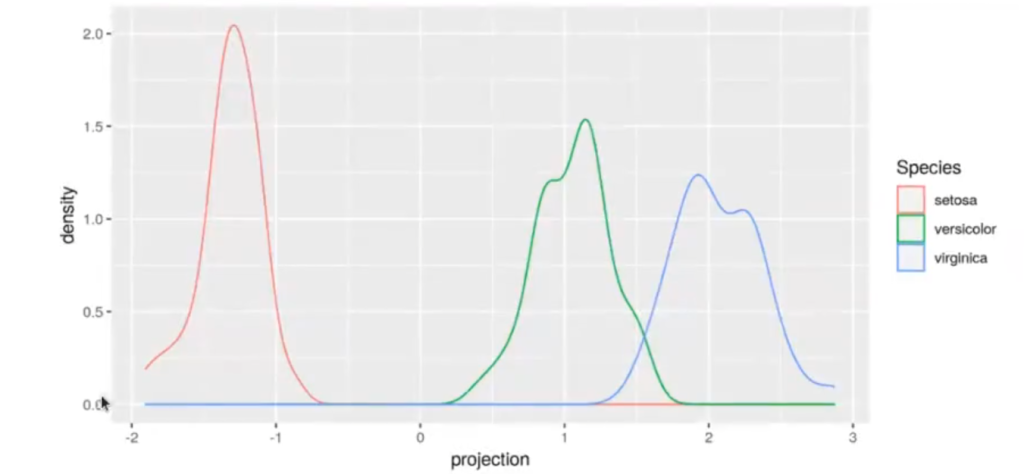
Para el conjunto de datos de entrenamiento:
X_test <- as.matrix (iris_test ( , 1 : 4]) iris_test$projection <- Re (X_test %*% W) ggplot (iris_test, aes (x = projection, color = Species)) + geom_density ()
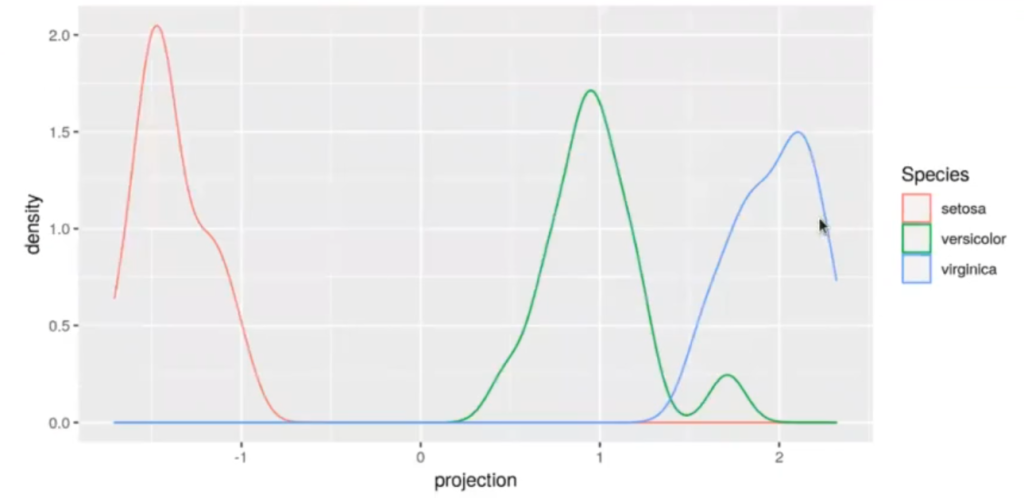
#Ejemplo de LDA para clases múltiples ld_iris <- predict (1, iris_train) df_ld_iris <- data.frame (ld_iris$x) df_ld_iris$Species <- iris_train$Species ggplot (df_ld_iris, aes (x = -LD1, y = LD2, color = Species)) + geom_point ()
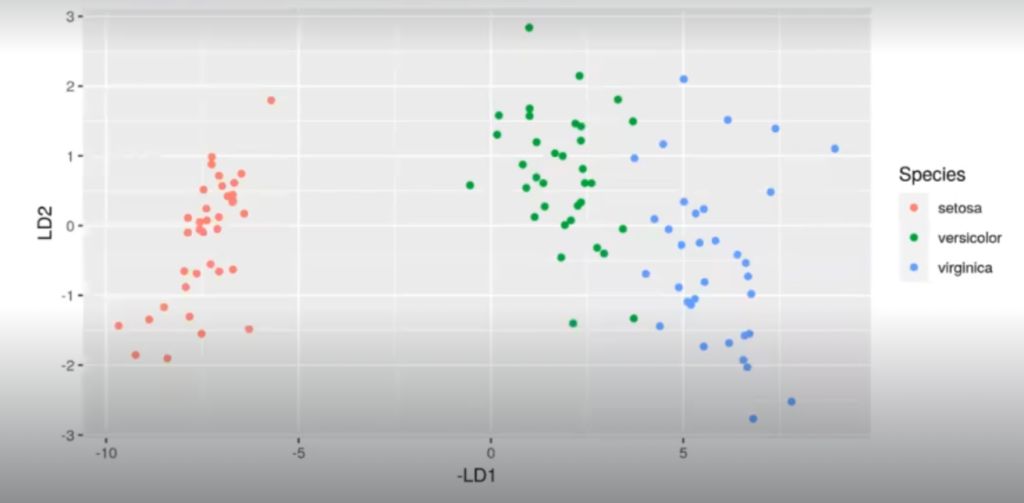
pred_test_iris <- predict (l, iris_test) pred_test_iris

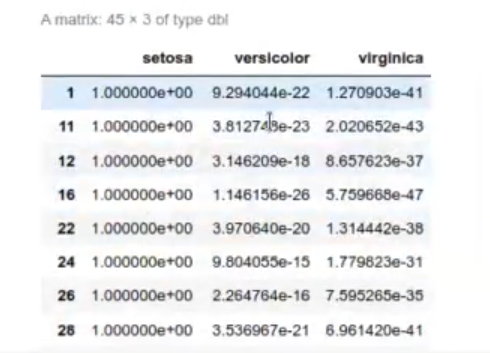
table (real = iris_test$Species, pred = pred_test_iris$class)

cf_m <- caret :: confusionMatrix (data = pred_test_iris$class, reference = iris_test$Species) cf_m
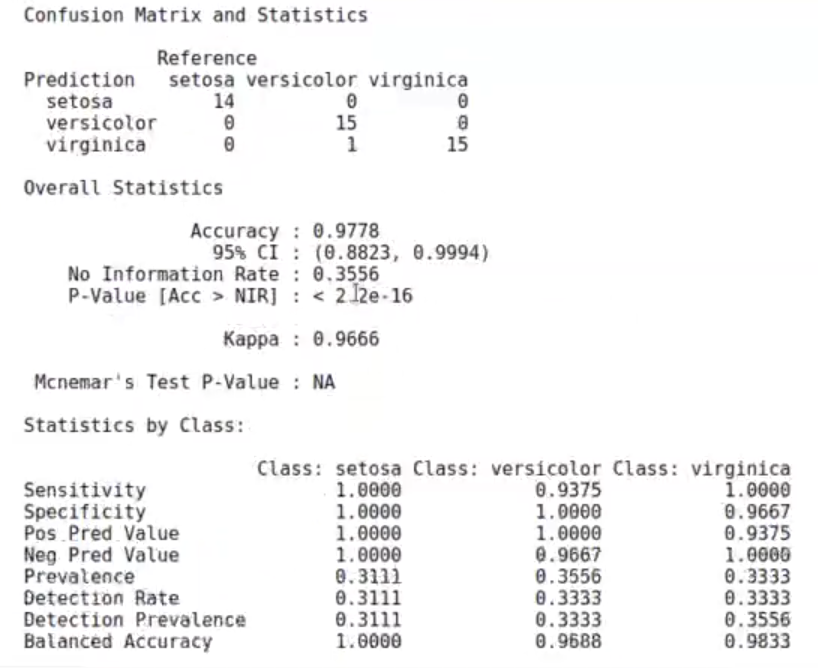
#Ejemplo de LDA para clases múltiples
paste ("La exhaustividad (recall, sensitivity) para Setosa:", cf_mstable [1, 1] / sum (cf_m$table [ ,1]))
paste ("La exhaustividad (recall, sensitivity) para Versicolor:", cf_m$table [2, 2] / sum (cf_mstable [ , 2]))
paste ("La exhaustividad (recall, sensitivity) para Virginica:", cf_mstable [3, 3] / sum (cf_m$table [ , 3]))
‘La exhaustividad (recall, sensitivity) para Setosa: 1’
‘La exhaustividad (recall, sensitivity) para Versicolor: 0.9375’
‘La exhaustividad (recall, sensitivity) para Virginica: 1’
paste ("La precisión (Pos Pred Value) para Setosa: ", cf_m$table [1, 1] / sum (cf_m$table[1, ]))
paste ("La precisión (Pos Pred Value) para Versicolor:", cf_mstable [2, 2] / sum (cf_m$table [2, ]))
paste ("La precisión (Pos Pred Value) para Virginica:", cf_m$table [3, 3] / sum (cf_m$table [3, ]))
‘La precisión (Pos Pred Value) para Setosa: 1’
‘La precisión (Pos Pred Value) para Versicolor: 1’
‘La precisión (Pos Pred Value) para Virginica: 0.9375’
Ahora que hemos visto cómo funciona el LDA con múltiples capas, podemos seguir aprendiendo sobre Big Data. Para ello, desde KeepCoding te invitamos a inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de tan solo 8 meses en la que adquirirás todos los conocimientos teóricos y prácticos necesarios para incursionar en un mercado laboral de buena rentabilidad y lleno de oportunidades. ¡Anímate a cambiar tu vida y solicita ya más información!











