Ejemplo del producto escalar en Python

El producto escalar en Python de dos vectores se define como la suma de los productos de sus elementos. Geométricamente, se entiende como el módulo de uno de ellos por la proyección de otro sobre él.

¿Qué es el producto escalar?

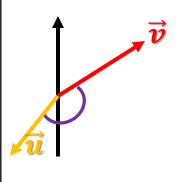
Tenemos este gráfico:

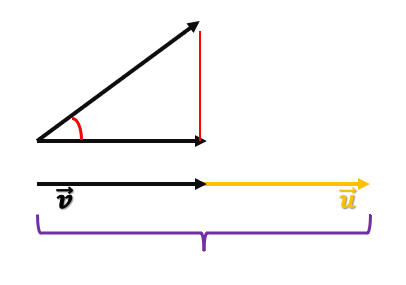
Veamos la fórmula matemática del producto escalar:

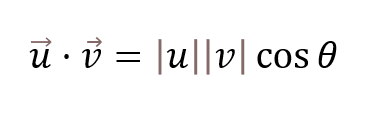
La fórmula matemática del producto escalar viene dada por los componentes de la anterior imagen. Tenemos, pues, el módulo del vector u o fórmula de producto vectorial (|u|), el módulo del vector v (|v|) y el ángulo entre ambos (cos θ).

¿De qué nos sirve esto? Esto es bastante importante, dado que nos da pie a introducir la similitud entre vectores o producto vectorial ejemplos, muy usada en machine learning.

Casos especiales donde es aplicable la fórmula matemática del producto escalar

Primer caso

Tenemos, por lo tanto, el vector v y el vector u. ¿Qué sucede con el producto escalar? ¿Será mayor, menor o igual a cero?

Si utilizamos la ecuación y decimos que tenemos dos vectores que son perpendiculares, ¿qué significa esto? Que el producto escalar será igual a 0.

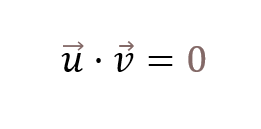
El producto escalar es igual a 0 porque, como son perpendiculares, el coseno del ángulo de 90° es 0.

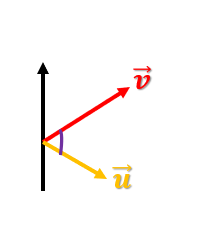
Segundo caso

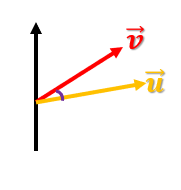
En este segundo caso tenemos dos vectores: el u y el v. En este caso el ángulo es menor a 90°, es decir, ambos vectores no son perpendiculares.

θ < 90°

¿Cuál será el resultado en esta situación? ¿El producto escalar será positivo, negativo…?

Una forma de ver esto es dibujando la ecuación del coseno:

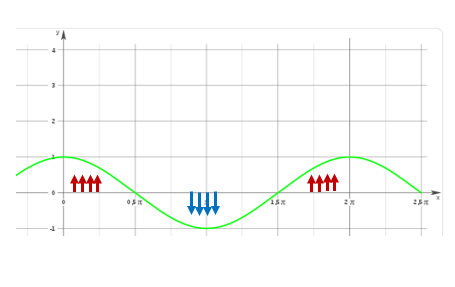
Aquí vemos que hay unas partes positivas (marcadas con flechas rojas) y unas partes negativas (marcadas con azul). Esto sería el coseno de θ.

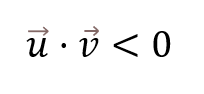
Lo que estamos viendo aquí es que, si el coseno es menor que 90, es positivo; por tanto, el producto escalar también va a ser positivo.

Tercer caso

Este tercer caso es un caso opuesto al anterior, ya que en esta ocasión el ángulo entre el vector v y el vector v es mayor que 90°. Bajo estas condiciones, el producto escalar va a ser negativo. Esto viene dado por la gráfica del coseno, donde podemos ver que, en los números con un ángulo menor que 90°, el producto escalar es positivo. Por el contrario, en ángulos mayores a 90° el producto escalar es negativo.

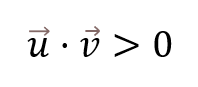
Ejemplo del producto escalar en Python

Veamos cómo funciona el producto escalar en Python.

Vamos a definir dos vectores, u y v:

#Ejemplo del producto escalar en Python
u = np.array ([20, 30, 40, 50])
v = np.array ([100, 200, 300, 400])

El producto escalar en Python puede calcularse usando el operador @:

u @ v

4000

El operador @ es válido únicamente para numpy arrays, no para listas:

#Ejemplo del producto escalar en Python
u_list = list (u)
v_list = list (v)

u_list @ v_list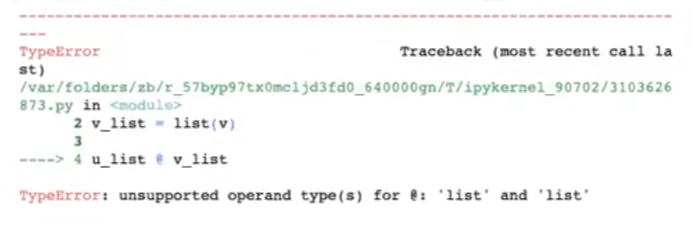

¿Qué sucede si introducimos vectores de distinto tamaño? Echándole un vistazo a la ecuación que define el producto escalar, podemos determinar el comportamiento que tendrá.

Ya hemos visto un poco la tendencia cuando hemos estado intentando entender ciertos tipos de errores. Esta tendencia consiste en que, si introducimos distintos tipos de arrays o realizamos el producto escalar con distintas dimensiones, no funciona.

Esto tiene sentido, porque con base en la ecuación que hemos visto, debería tener el mismo número de componentes.

#Ejemplo del producto escalar en Python
a_np = np.array ([1, 2])
b_np = np.array ([3, 4, 6])

a_np @ b_np

Por ende, el error que nos aparece es el anterior, en donde dice que, en efecto, el tamaño de la matriz 1 es diferente al de la matriz 2.

Ejercicio

Vamos a ver un ejercicio relacionado con el tema. A continuación, calculamos el producto escalar en Python de dos vectores sin usar numpy. Los vectores son u = [1, 3, 5, 7] y v = [2, 4, 6, 8].

Lo primero que haremos, como siempre, es definir los dos vectores.

Luego establecemos una lista vacía para almacenar el resultado y, posteriormente, iteramos sobre ambos vectores al mismo tiempo.

Por último hacemos una multiplicación de vectores ejemplos:

#Ejercicio del producto escalar en Python
u = [1, 3, 5, 7]
v = [2, 4, 6, 8]

res = [ ]
for i, k in zip (u, v):
res.append (i * k)

print (res)

[2, 12, 30, 56]

Esto nos dio una lista con la multiplicación de cada valor.

Pero no es el producto escalar, ya que el producto escalar en su definición tiene una suma, que haremos del siguiente modo, para que nos dé el valor final:

#Ejercicio del producto escalar en Python
u = [1, 3, 5, 7]
v = [2, 4, 6, 8]

res = [ ]
for i, k in zip (u, v):
res.append (i * k)

sum (res)

100

Lo podríamos hacer de una forma más compacta con las listas de compresión:

u = [1, 3, 5, 7]
v = [2, 4, 6, 8]

sum (u [i] * v [i] for i in range (lem (u)))

100

Aquí lo que hemos hecho es iterar sobre la longitud del vector u para variar un poco. Esto nos permite obtener los componentes de ambos vectores al mismo tiempo.

Ahora codificaremos unas líneas en las que se nos imprimirán los índices de los componentes del vector u:

for i in range (len (u)):
print (i)

0

1

2

3

O incluso mejor aún:

sum (np.array (u) * np.array (v))

100

Veamos otra forma más de hacer este ejercicio:

u_np = np.array ([1, 3, 5, 7])
v_np = np.array ([2, 4, 6, 8])

np.dot (u_np, v_np)

100

¿Quieres seguir aprendiendo?

Ahora que hemos visto cómo funciona el producto escalar en Python, podemos seguir aprendiendo sobre Big Data, una de las disciplinas más demandadas de la actualidad. Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que podrás adquirir todos los conocimientos teóricos y prácticos que se necesitan para incursionar en el mercado laboral de forma rápida y eficiente.¡Cambia tu futuro y solicita más información!