Ejemplo estadístico de test de embarazo

Llevar a cabo análisis aleatorios como un ejemplo estadístico de test de embarazo te ayudarán a comprender cómo funciona un estudio de probabilidad para el manejo de los macrodatos. Por ello, en este post, te exponemos un completo ejemplo estadístico de test de embarazo.

Ejemplo estadístico de test de embarazo

Para este ejemplo estadístico de test de embarazo, hay que partir de que un test de embarazo tiene una posibilidad de acierto del 99%. Si nuestro sujeto utiliza su orín para probar 100 tests de embarazo, ¿cuál es la probabilidad de que al menos un test de embarazo salga positivo?

Sabiendo que, para este ejemplo, dicho sujeto es un hombre y no puede quedarse embarazado, esto se resolvería utilizando la función de una binomial:

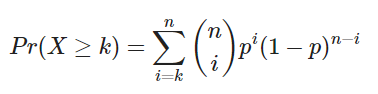
Donde:

• n = 100
• k = 1
• p = 0.01

Este ejemplo estadístico de test de embarazo en R se haría:

n=100
k=1
p=0.01

1-dbinom(x=0,size=100,prob=0.01)
#dbinom(x=1,size=100,prob=0.01)
#dbinom(x=2,size=100,prob=0.01)
#dbinom(x=3,size=100,prob=0.01)
#dbinom(x=4,size=100,prob=0.01)

0.633967658726771

probFinal<-0
for (x in k:n){    
    probFinal<-probFinal+dbinom(x=x,size=100,prob=0.01)
}
print(paste0("La probabilidad de que en ",n," tests de embarazo salga al menos ",
             k," indicando embarazo, es del ",round(probFinal*100,2),"%"))

[1] “La probabilidad de que en 100 tests de embarazo salga al menos 1 indicando embarazo, es del 63.4%”
Lo cual significa que hay más posibilidades de que al hacer este ejemplo estadístico de test de embarazo salga alguno con un falso positivo, es decir, que diga que este hombre está embarazado.

Los tests de embarazo miden el nivel de la hormona hCG en la orina, el problema seguramente esté en que esta probabilidad de error viene dado porque algunas veces (pocas) la presencia de esta hormona en la orina de una mujer no implica que esté embarazada. Nuestro sujeto hombre no va a tener esa hormona, lo que indica que la probabilidad de que un test de embarazo falle en su caso es mucho menor.

NOTA: esto se podría calcular de forma más fácil asumiendo que tenemos n = 100 sucesos independientes con probabilidad (1 – p) . La probabilidad de que absolutamente todos los tests dieran un resultado correcto es de 0.99^100 = 0.366, con lo que la posibilidad de que al menos un test falle es 1 – 0.366 = 0.634. De hecho, si en la ecuación de la binomial utilizas k = 0 la ecuación queda reducida a:

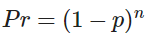
¿Te puedes fiar de este resultado?

En este ejemplo estadístico de test de embarazo se simula que el experimento en R y repetirlo 10.000 veces para poder calcular probabilidades.

La función rbinom(n,size=1,prob=p) genera un vector de tamaño n = 100, donde cada elemento sigue una distribución de Bernouilli (size = k = 1).

p=0.01
n=100
k=1

experimento<-runif(n,min=0,max=1)<p

experimento

1. FALSE
2. FALSE
3. FALSE
4. FALSE
5. FALSE
6. FALSE
7. FALSE
8. TRUE
9. FALSE
10. FALSE
11. FALSE
12. FALSE
13. FALSE
14. FALSE
15. FALSE
16. FALSE
17. FALSE
18. FALSE
19. FALSE
20. FALSE
21. FALSE
22. FALSE
23. FALSE
24. FALSE
25. FALSE
26. FALSE
27. FALSE
28. FALSE
29. FALSE
30. FALSE
31. FALSE
32. FALSE
33. FALSE
34. FALSE
35. FALSE
36. FALSE
37. FALSE
38. FALSE
39. FALSE
40. FALSE
41. FALSE
42. FALSE
43. FALSE
44. FALSE
45. FALSE
46. FALSE
47. TRUE
48. FALSE
49. FALSE
50. FALSE
51. FALSE
52. FALSE
53. FALSE
54. FALSE
55. FALSE
56. FALSE
57. FALSE
58. FALSE
59. FALSE
60. FALSE
61. FALSE
62. FALSE
63. FALSE
64. FALSE
65. FALSE
66. FALSE
67. FALSE
68. FALSE
69. FALSE
70. FALSE
71. FALSE
72. FALSE
73. FALSE
74. FALSE
75. FALSE
76. FALSE
77. FALSE
78. FALSE
79. FALSE
80. FALSE
81. FALSE
82. FALSE
83. TRUE
84. FALSE
85. FALSE
86. FALSE
87. FALSE
88. FALSE
89. FALSE
90. FALSE
91. FALSE
92. FALSE
93. FALSE
94. FALSE
95. FALSE
96. FALSE
97. FALSE
98. FALSE
99. FALSE
100. FALSE

numTestFail<-0
totalIntentos<-10000
p=0.01
n=100
k=1
for (i in 1:totalIntentos){
    #experimento<-rbinom(n,size=1,prob=p)
    experimento<-runif(n,min=0,max=1)<p
    numFalsoPositivo<-sum(experimento)
    if (numFalsoPositivo>=k){
        numTestFail<-numTestFail+1
    }
}
probFinal=numTestFail/totalIntentos
print(paste0("La probabilidad de que en ",n," tests de embarazo salga al menos ",
             k," indicando embarazo, es del ",round(probFinal*100,2),"%"))

[1] “La probabilidad de que en 100 tests de embarazo salga al menos 1 indicando embarazo, es del 63.09%”

¿Quieres conocer más sobre el Big Data?

En este post te hemos expuesto un gran ejemplo estadístico de test de embarazo con el que has podido notar cómo funciona la probabilidad en un estudio de estadística para manejo Big Data.

Si quieres aprender más sobre el Big Data, en KeepCoding contamos con el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Durante el desarrollo de este bootcamp, comprenderás que todo buen data scientist debe tener una amplia y sólida base de estadística, así como también es muy importante la base de álgebra, cálculo y geometría. Todo ello se lleva a cabo de la mano de expertos en el mundo del manejo del Big Data y sus alternativas. ¡No esperes más para inscribirte!