Un ejemplo de problemas de optimización en TensorFlow te ayuda a enfrentarte a cómo funcionan los facilitadores de este framework, de manera que puedas comprender la forma en la que se implementan en el procesamiento de los macrodatos dentro del Deep Learning.
En efecto, en el manejo del Big Data, estos procesos se presentan como un conocimiento base de un buen data scientist. Por ello, en este post, te exponemos un ejemplo de problemas de optimización en TensorFlow.
Ejemplo de problemas de optimización en TensorFlow
Como primera instancia, antes de presentar el ejemplo de problemas de optimización en TensorFlow, hay que partir de que una red neuronal no es otra cosa que un optimizador de funciones.
Para entender para qué podríamos utilizar este optimizador de funciones, a continuación te mostramos un ejemplo de problemas de optimización en TensorFlow. Para este ejemplo, piensa que Netflix ha decidido colocar otro de sus famosos carteles publicitarios en un edificio.

Han decidido que el cartel publicitario tiene que cubrir una superficie de 600 metros cuadrados, dejando un margen de 2 metros arriba y abajo y de 4 metros a izquierda y derecha para publicidad. Sin embargo, no te han comunicado las dimensiones de la fachada del edificio. Podríamos mandar un email al propietario y preguntarle, pero como sabemos matemáticas, podemos ahorrárnoslo. ¿Cómo podemos averiguar las dimensiones del edificio?
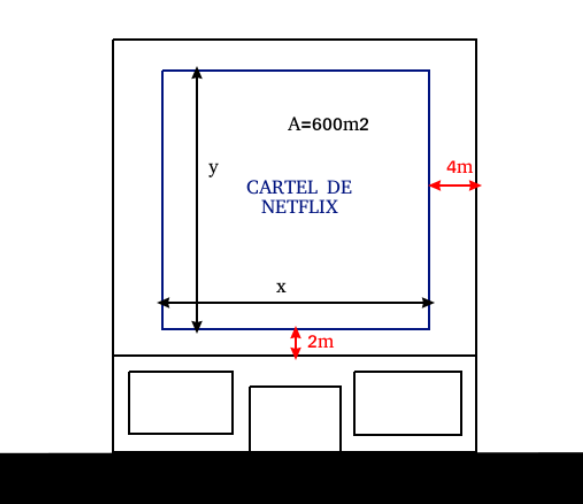
Veamos, la superficie completa del edificio será:
Ancho = 4 + x + 4 = x + 8
Alto = 2 + y + 2 = y + 4
S = Ancho x Alto = (x+8)(y+4)
Y tenemos la condición de que: xy = 600
Esto nos permite formar un sistema de ecuaciones, en el que sustituimos:
xy = 600 -> x = 600/y
S(y) = ( 600/y + 8)(y+4) = 600 + 8y + 4·600/y + 32 = 632 + 8y + 2400/y
En un problema de optimización, se utiliza la información de la pendiente de la función, es decir, la derivada, para calcular su mínimo. Tenemos que igualar la primera derivada a 0 y luego comprobar que la segunda derivada es positiva. Así, en este caso:
S'(y) = 8-2400/y²
S»(y) = 4800/y³
S'(y) = 0 -> 0 = 8-2400/y² -> 8 = 2400/y² -> y² = 2400/8 = 300 -> y = sqrt(300) = sqrt(100 · 3) = sqrt(100)·sqrt(3) = 10·sqrt(3) = 17.32 (descartamos el signo negativo por no tener sentido físico)
Sustituyendo en x:
x = 600 / 10·sqrt(3) = 60 / sqrt(3) = 60·sqrt(3) / sqrt(3)·sqrt(3) = 60·sqrt(3) / 3 = 20·sqrt(3) = 34.64
Como para y = 17.32 -> S»(y) = 0.9238 > 0, hemos encontrado la solución mínima.
Con lo cual, las dimensiones del edificio son:
Ancho: x + 8 = 42.64 m
Alto: y + 4 = 21.32 m
¿Habéis visto lo útiles que son las derivadas? Acabamos de solucionar este problema analíticamente. Lo hemos hecho así porque es sencillo y podemos, pero existen muchos problemas para los que es muy costosos computacionalmente costoso solucionarlos de forma analítica, por lo que se emplean métodos numéricos. Uno de estos métodos es el descenso del gradiente.
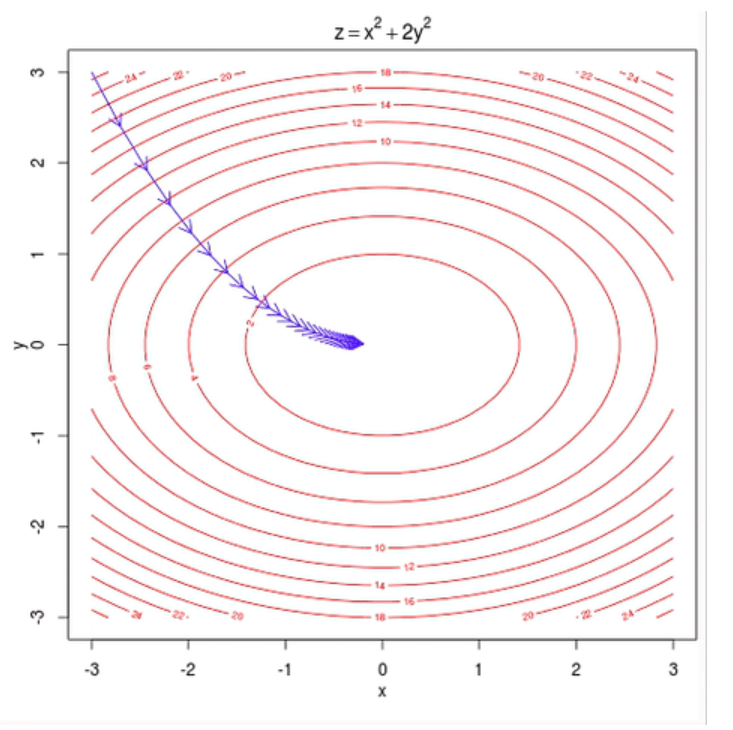
Veamos rápidamente con un ejemplo qué es el descenso del gradiente.
El descenso del gradiente es el mecanismo que hace que una red neuronal aprenda. Al fin y el cabo, podemos ver el descenso del gradiente como un algoritmo de optimización que permite minimizar cualquier función (siempre que sea diferenciable, es decir, que podamos calcular sus derivadas).
¿Quieres aprender más sobre el Big Data?
En este post, te has podido enfrentar a un ejemplo de problemas de optimización en TensorFlow, de manera que te recomendamos practicar con él y acoplarlo a los intereses de tu procesamiento de los macrodatos. No obstante, existen muchas más alternativas para el manejo del Big Data, ¿quieres aprender más sobre ellas?
Nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning te permitirá consolidar tus conocimientos y poner a prueba tus destrezas en este ámbito de transformaciones y acciones en Spark. En el transcurso de esta formación intensiva, aprenderás a utilizar sus métodos de inteligencia artificial, aprendizaje automático, estadística y sistemas de bases de datos. ¡No lo dudes más, matricúlate y empieza ahora!







