En este post veremos algunos ejemplos de fractales en Python.

Ejemplos de fractales en Python

Primer ejemplo

Veamos algunos ejemplos de fractales en Python:

#Ejemplos de fractales en Python
import matplotlib.pyplot as plt
import random

def regla1 (1):
       x = p [0]
       y = p [1]
       return x + 1, y - 1

def regla2 (p):
       x = p [0]
       y = p [1]
       return x + 1, y - 1

def transformacion (p):
       #Incluimos todas las reglas de transformación
       lista_reglas = [regla1, regla2]
       #Elegimos aleatoriamente una función
       t = random.choice [lista_reglas]
       #Aplicamos la regla elegida
       x, y = t (p)
       #Devolvemos los nuevos valores
       return x, y

#Ejemplos de fractales en Python
def trayectoria (p, n)
       x = [p [0]]
       y = [p [1]]
       for i in range (n):
             p = transformacion (p)
             x.append (p [0])
             y.append (p [1])
       return x, y

#Punto inicial
p = (1, 1)
n = int (input ('Número de iteraciones: '))
x, y = trayectoria (p, n)
#Dibujo
plt.plot (x, y)
plt.xlabel ('X')
plt.ylabel ('y')
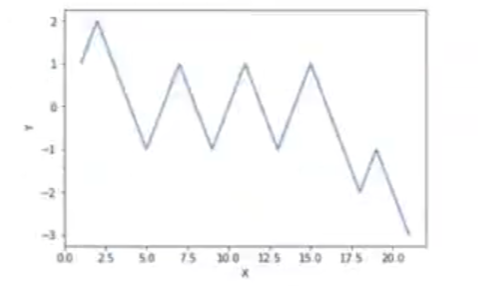
plt.show ()

Número de iteraciones: 20

El helecho de Barnsley (Barnsley Fern)

El helecho de Barnsley es un fractal que lleva el nombre del matemático británico Michael Barnsley, quien lo describió por primera vez en su libro Fractales en todas partes (2012) o Fractals everywhere.

Usando aplicaciones repetidas de una transformación simple en un punto, se pueden construir objetos de Barnsley.

Propuso los siguientes pasos para crear estas estructuras. Comenzamos con el punto (0, 0) y seleccionamos aleatoriamente una de las siguientes transformaciones con la probabilidad asignada:

• Regla 1 (Probabilidad 0.85)
  • x_n+1 = 0.85x_n + 0.04y_n
  • y_n+1 = 0.04y_n + 0.85y_n + 1.6
• Regla 2 (Probabilidad 0.07)
  • x_n+1 = 0.2x_n – 0.26y_n
  • y_n+1 = 0.23y_n + 0.22y_n + 1.6
• Regla 3 (Probabilidad 0.07)
  • x_n+1 = -0.15x_n – 0.28y_n
  • y_n+1 = 0.26y_n + 0.24y_n + 0.44
• Regla 4 (Probabilidad 0.01)
  • x_n+1 = 0
  • y_n+1 = 0.16y_n

#Ejemplos de fractales en Python
import random
import matplotlib.pyplot as plt

def transformation_1 (p):
       x = p [0]
       y = p [1]
       x1 = 0.85 * x + 0.04 * y
       y1 = -0.04 * x + 0.85 * y + 1.6
       return x1, y1

def transformation_2 (p):
       x = p [0]
       y = p [1]
       x1 = 0.2 * x - 0.26 * y
       y1 = 0.23 * x + 0.22 * y + 1.6
       return x1, y1

def transformation_3 (p):
       x = p [0]
       y = p [1]
       x1 = -0.15 * x - 0.28 * y
       y1 = 0.26 * x + 0.24 * y + 0.44
       return x1, y1

def transformation_4 (p):
       x = p [0]
       y = p [1]
       x1 = 0
       y1 = 0.16 * y
       return x1, y1

#Ejemplos de fractales en Python
def get_index (probability):
r = random.random ()
c_probability = 0
sum_probability = [ ]
for p in probability:
      c_probability += p
      sum_probability.append (c_probability)
for item, sp in enumerate (sum_probability):
      if r <= sp:
            return item
return len (probability) -1

def transform (p):
      #Lista de las transformaciones
      transformations = [transformation_1, transformation_2, transformation_3, transformation_4]
      probability = [0.85, 0.07, 0.07, 0.01]
      #Elegimos una transformación al azar y la llamamos
      tindex = get_index (probability)
      t = transformation (tindex)
      x, y = t (p)
      return x, y

def draw_fern (n):
      #Empezamos en (0, 0)
      x = [0]
      y = [0]
      x1, y1 = 0, 0
      for i in range (n):
            x1, y1 = transform ((x1, y1))
            x.append (x1)
            y.append (y1)
      return x, y

n = int (input ('Introduce el número de puntos: '))
x, y = draw_fern (n)

#Ejemplos de fractales en Python
#Graficamos
plt.plot (x, y, ' o ')
plt.title ('Helecho con {0} puntos'.format (n))
plt.show ()

Introduce el número de puntos: 500000

¿Cómo continuar?

Ahora que hemos visto cómo funciona la estructura de un espacio vectorial, puedes seguir aprendiendo sobre Big Data, una de las disciplinas más demandadas y mejor pagadas hoy en día. Para ello, entra a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación intensiva en la que podrás adquirir todos los conocimientos, tanto teóricos como prácticos, necesarios para entrar en el mercado laboral en pocos meses. ¡Anímate a impulsar tu carrera y solicita más información!