En este artículo veremos un ejercicio de aplicación de clustering con los tipos de aceite.
Ejercicio de aplicación de clustering
Lo primero que haremos en nuestro ejercicio de aplicación de clustering será usar un paquete caret para estandarizar:
- caret :: preProcess (olive, method = c («center», «scale»))
También tenemos ya el aceite de oliva estandarizado:
- olive_standarized = predict (standarized_model, olive)
Posteriormente, calcularemos la matriz de distancia con:
- d <- dist (as.matrix (olive_standarized), metod = «euclidean»)
Y acto seguido pintamos el dendrograma:
library (dslabs)
standarized_model <- caret :: preProcess (olive, method = c ("center", "scale"))
olive_standarized = predict (standarized_model, olive)
d <- dist (as.matrix (olive_standarized), metod = "euclidean")
hc <- hclust (d, method = "average")
hcd <- as.dendrogram (hc)
plot (color_branches (hcd, k = 5), leaflab = "none")
abline (h = 4.42, col = "red")Warning message in dist (as.matrix (olive_standarized), method = «euclidean»): «NAs introduced by coercion»
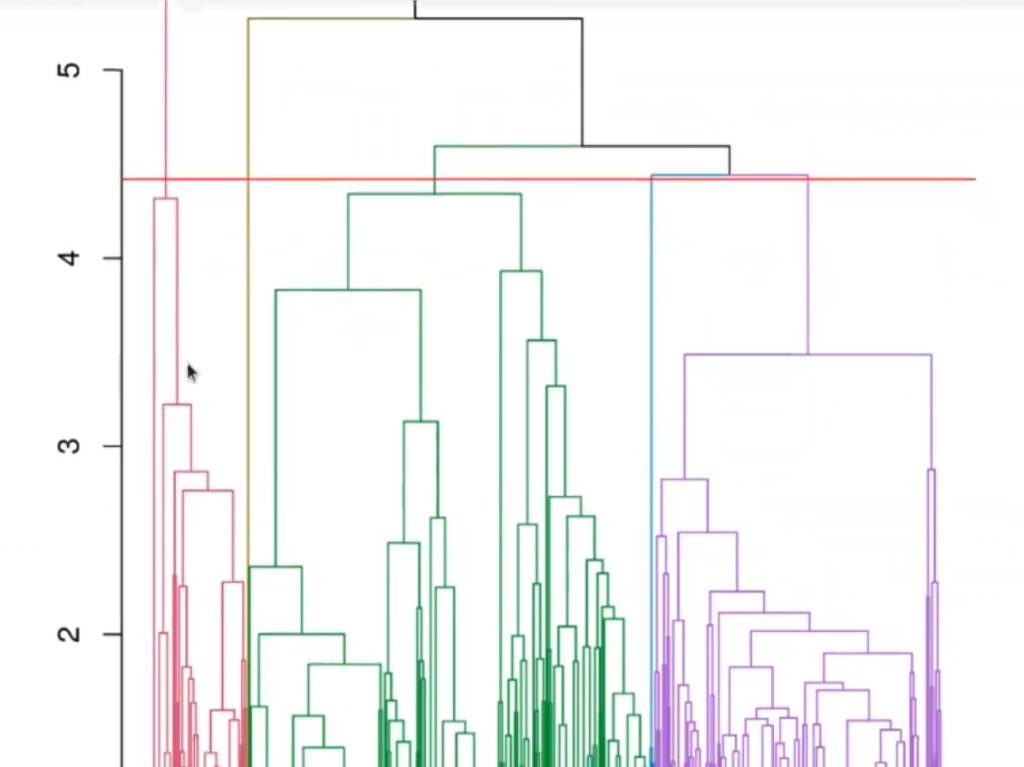
Si nos fijamos, aquí se ha puesto el umbral en 4.42. ¿Por qué en 4.42? Porque es lo mejor para no tener muchos clústeres (5 en total con el umbral).
Podríamos haber tenido un poco más de clústeres, digamos 6, pero resulta que al bajar la primera rama (color rojo) se dividiría en 2, la segunda rama (color verde) también se habría dividido en 2.
Asimismo, podríamos haber subido un poco más, pero en este caso nos habríamos quedado con 3, que ya son muy pocos clústeres.
Esto es un poco intuitivo y a gusto de quien esté realizando el ejercicio de aplicación de clustering.
Vamos, por tanto, a analizar un poco lo que hemos hecho.
Aquí tenemos la distancia, el hc. El hc calcula el clúster jerárquico.
Así pues, le estamos diciendo al algoritmo que nos enseñe las alturas que superen el 4.42 (donde está el umbral).
hc$height [hc$height >= 4.42]4.44157833878639 . 4.59542858089067 . 5.27461231626934 . 5.44318196042116
¿Qué significan estos números? Estos son los puntos en los que se van a unir los clústeres que tenemos ahora.
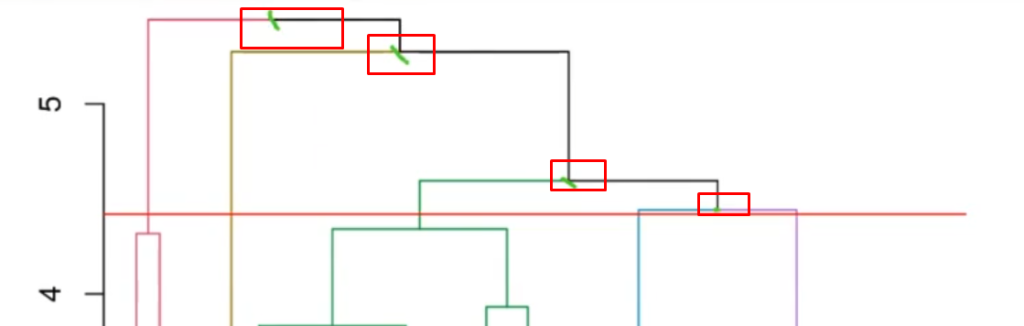
Estos valores se pueden ver reflejados en el dendrograma que habíamos pintado anteriormente en nuestro ejercicio de aplicación de clustering.
Podemos usar cutree con el dendrograma.
# cl <- cutree (hc, k = 5)
cl <- cutree_1h.dendrogram (hcd, h = 4.42)
olive$cluster = factor (cl)
summary (olive)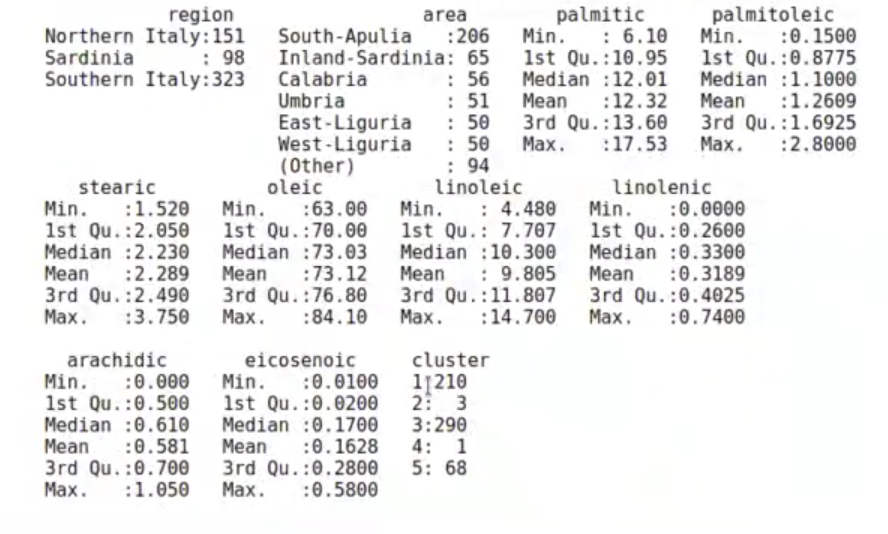
El resultado nos muestra que el clúster 2 tiene 3 elementos y que el clúster 4 tiene solo 1.
¿Qué es lo que ocurre? Que ahora realmente solo tenemos tres clústeres (rojo, verde y morado), que a lo mejor es un número bastante bajo.
Si cambiamos el 4.42 por el 4.3, nos aparecen más clústeres:

Tenemos muchos clústeres y varios de ellos tienen sentido.
Aunque realmente lo que tendríamos que haber hecho y modificado es la línea de código: hc <- hclust (d, method = «average») y, en vez de haber puesto «average», tendrímos que haber puesto «complete». De este modo, el dendrograma habría cambiado también:

Y el código completo habría quedado así:
library (dslabs)
standarized_model <- caret :: preProcess (olive, method = c ("center", "scale"))
olive_standarized = predict (standarized_model, olive)
d <- dist (as.matrix (olive_standarized), metod = "euclidean")
hc <- hclust (d, method = "complete")
hcd <- as.dendrogram (hc)
plot (color_branches (hcd, k = 5), leaflab = "none")
abline (h = 4.42, col = "red")En este caso, podemos ver que el average hace mejor una separación de los clústeres. Ya sabemos que en este ejercicio de aplicación de clustering, así como en cualquier otro tipo de ejercicios, lo importante es ir probando a ver qué nos funciona. Y no solo qué funciona, sino qué funciona mejor y de manera más óptima.
Podemos pintar el silhouette:
library (cluster)
ss <- silhouette (cl, d)
plot (ss, col = 1 : max (cl), border = NA)
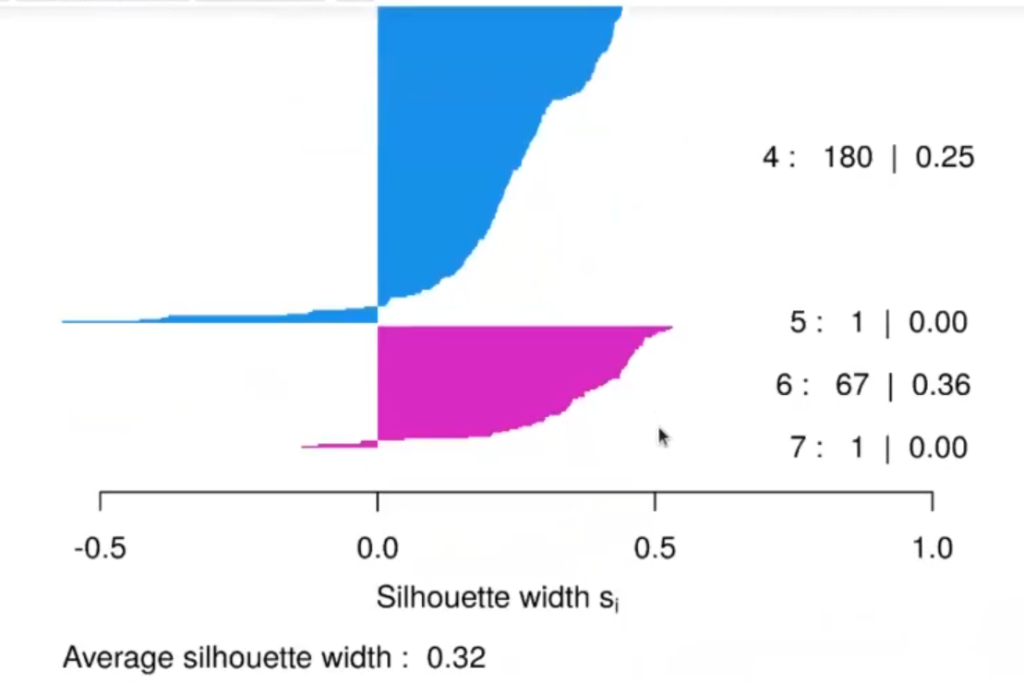
Este silhouette nos muestra los 7 clústeres que hay. En algunos el valor no es muy bueno y esto se ve representado por las pequeñas líneas que hay al lado izquierdo del silhouette.
Al parecer, el clúster 2 es bastante fiable, pero tiene solo 3 elementos.
A continuación, lo que haremos será buscar dónde están ubicados cada uno de los clústeres:
olive %>% filter (cluster == 1) %>% summary ()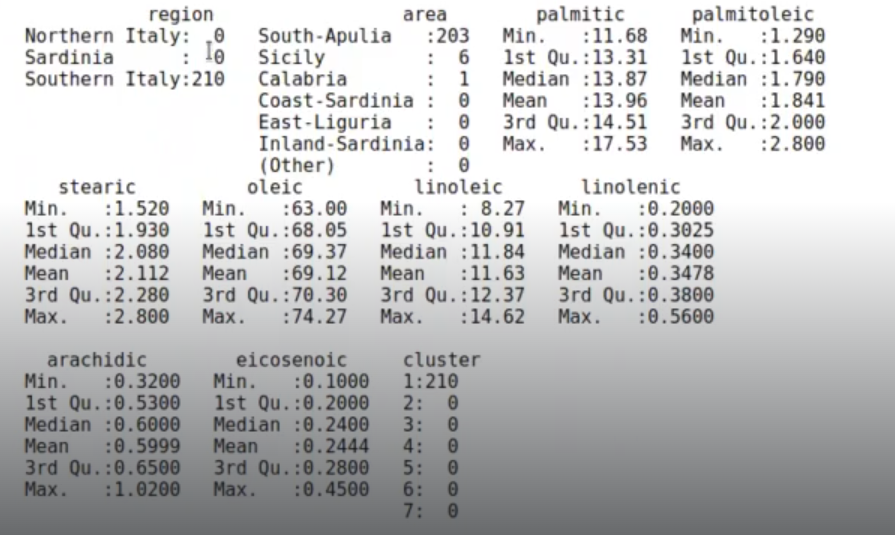
olive %>% filter (cluster == 2) %>% summary ()
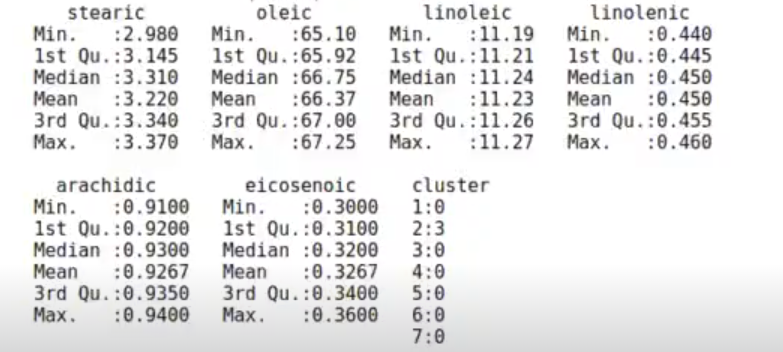
olive %>% filter (cluster == 3) %>% summary ()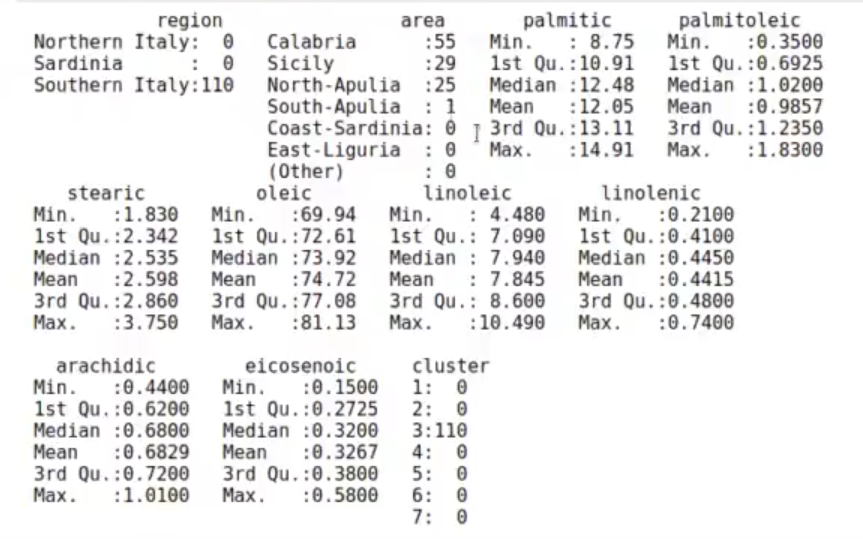
olive %>% filter (cluster == 4) %>% summary ()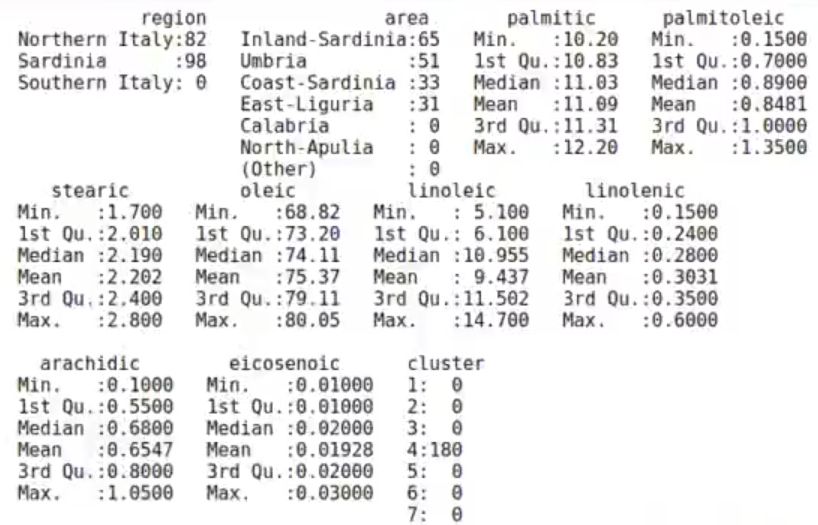
#Ejercicio de aplicación de clustering: cierre
olive %>% filter (cluster == 5) %>% summary ()
Ahora que hemos visto, por medio de un ejercicio de aplicación de clustering cómo funciona este elemento de agrupamiento, podemos dar un paso más allá para seguir aprendiendo. Para ello te invitamos a acceder a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que, en muy pocos meses, podrás adquirir todos los conocimientos necesarios para incursionar en el mundo del Big Data. ¡Anímate a cambiar tu vida y solicita más información!











