En este artículo desarrollaremos un ejercicio de boosted trees o gradient boosting.
Recordemos que los boosted trees son la modificación del árbol de decisión, ya que el número de árboles necesarios es mayor y, por tanto, los datos de entrenamiento serán más precisos.
El entrenamiento del algoritmo de boosting requiere fijar tres parámetros libres:
- Número de iteraciones
- Tasa de aprendizaje (a)
- Complejidad del árbol: max_depth
Se podría hacer una búsqueda sobre los tres parámetros conjuntamente mediante GridSearchCV, sin embargo, es muy costoso a nivel computacional, por lo que es más sencillo aplicar una optimización de forma secuencial: se prueban distintos valores de los parámetros libres, se fijan los óptimos y se busca sobre el resto.
Ejercicio de boosted trees
#Ejercicio de boosted trees
from sklearn.ensemble import Gradient BoostingClassifier
Niterations = [25, 50, 75, 100, 125, 150, 175, 200, 300]
learningRate = [0.5, 0.1, 0.05, 0.01]
#mantenemos max depth estático: max_depth = 2
param grid = {'n estimators': Niterations, 'learning_rate': learningRate }
grid = GridSearchCV (GradientBoostingClassifier (random_state = 0, max_depth = 2), param_grid = param_grid, cv = 5, verbose = 1)
grid.fit (X_train, y_train)
print ("best mean cross - validation score: { : . 3f}".format (grid.best_score_)
print("best parameters: {}".format (grid.best_params_))Fitting 5 folds for each of 36 candidates, totalling 180 fits
[Parallelin jobs = 1)]: Using backend SequentialBackend with 1 concurrent workers.
best mean cross-validation score: 0.761
best parameters: {‘learning_rate»: 0.01, ‘n_estimators’: 200]
[Parallel (n_jobs=1)]: Done 180 out of 180 elapsed: 16.6s finished
Representemos el error que estamos cometiendo para los distintos valores de los parámetros libres:
#Ejercicio de boosted trees
#calculamos métricas globales
IrOptimo = grid.best_params_ ['learning_rate']
neOptimo = grid.best_params ['n_estimators']
bt = GradientBoostingClassifier (random_state = 0, max_depth = 2, learning_rate = lrOptimo, n_estimators = neOptimo)
bt.fi t(x_train, y_train)
error = 1 - grid.cv_results_ ['mean_test_score'].reshape (len (learningRate), len (Niterations)) colors = ['r', 'b', 'g', 'k', 'm']
for i, lr in enumerate(learningRate):
plt.plot (Niterations, error [ i, : ], colors [ i ] + ' - - o ', label = 'Ir = %g' %lr)
plt. legend ()
plt.xlabel ('# iteraciones")
plt.ylabel ('5 - fold CV Error')
plt.title ('train: %0.3f \ ntest: %0.3f' % (bt.score (X_train, y_train).bt.score (x_test, y_test)))
plt.grid ()
plt.show ()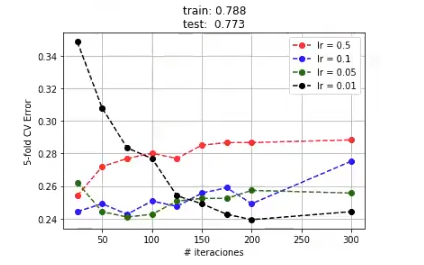
Las prestaciones no son mucho mejores que con respecto a un árbol sencillo. Como el coste de entrenamiento de este conjunto no es muy grande, replicaremos el análisis anterior aumentando el valor de la complejidad.
#Ejercicio de boosted trees
Niterations = [25, 50, 75, 100, 125, 150, 175, 200, 300]
learningRate = [0.5, 0.1, 0.05, 0.01]
#mantenemos max depth estático: max_depth = 3
param_grid = {'n_estimators': Niterations, 'learning_rate': learningRate }
grid = GridSearchCV (GradientBoostingClassifier (random_state = 0, max_depth = 3), param_grid = param_grid, cv = 5)
grid.fit (x_train, y_train)
print ("best mean cross - validation score: { : . 3f}".format (grid.best_score_))
print ("best parameters: { }".format (grid.best_params_))best mean cross-validation score: 8.757
best parameters: [«learning_rate'»‘: 0.05, n_estimators: 100]
#Ejercicio de boosted trees
#calculamos métricas globales
lrOptimo = grid.best_params_ ['learning_rate']
neOptimo = grid.best_params_ ['n_estimators']
bt = GradientBoostingClassifier (random_state = 0, max_depth = 3, learning_rate = lrOptimo, n_estimators = neOptimo
bt.fit (x_train, y_train)
error = 1 - grid.cv_results_ ['mean_test_score'].reshape (len (learningRate), Ien (Niterations))
colors = ['r', 'b', 'g', 'k', 'm']
for i, lr in enumerate (learningRate):
plt.plot (Niterations, error [ i , : ], colors [ i ] + ' - - o ', label = 'lr = %g' %lr)
plt.legend ()
plt.xlabel ('# iteraciones")
plt.ylabel ('5 - fold CV Error")
plt.title ('train: %0.3f \ ntest: %0.3f'% (bt.score (X_train, y_train), bt.score (X_test, y_test)))
plt.grid ()
plt.show ()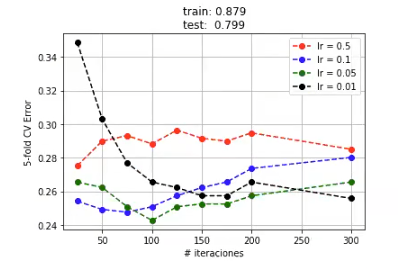
Vemos que, al aumentar la complejidad, necesitamos una tasa de aprendizaje más pequeña. En general, cuanto más complejo es el problema, menor es la taza de aprendizaje y mayor el número de iteraciones que necesita el algoritmo. Parece que podemos ir un poco más allá, así que disminuyamos un poco más la tasa de aprendizaje:
#Ejercicio de boosted trees
Niterations = [100, 125, 150, 175, 200, 300, 500]
learningRate = [0.05, 0.01, 0.005]
#mantenemos max depth estático: max_depth = 3
param_grid {'n estimators: Niterations, 'learning_rate': learningRate }
grid = GridSearchCV (GradientBoostingClassifier (random_state = 0, max_depth = 3), param_grid = param_grid, cv = 5)
grid.fit (x_train, y_train)
print ("best mean cross - validation score: { : . 3f}".format (grid.best_score_))
print ("best parameters: ".format (grid.best_params_))best mean cross – validation score: 0.757
best parameters: [‘learning_rate’: 0.05, ‘n_estimators’: 100]
#Ejercicio de boosted trees
#calculamos métricas globales
lrOptimo = grid.best_params ['learning_rate']
neOptimo = grid.best_params ['n_estimators ]
bt = GradientBoostingClassifier (random_state = 0, max_depth = 3, learning_rate = lrOptimo, n_estimators = neOptimo)
bt.fit (x_train, y_train)
error = 1 - grid.cv_results ['mean_test_score].reshape (len (learningRate), len (Niterations))
colors = ['r', 'b', 'g', 'k', 'm']
for i, lr in enumerate (learningRate):
plt.plot (Niterations, error [ i, : ], colors [ i ] + ' - - o ', label = 'lr = %g' %lr)
plt.legend ()
plt.xlabel ('# iteraciones")
plt.ylabel (5 - fold CV Error)
plt.title ('train: %0.3f\ntest: %0.3f'% (bt.score (X_train, y_train), bt.score (X_test, y_test)))
plt.grid ()
plt.show ()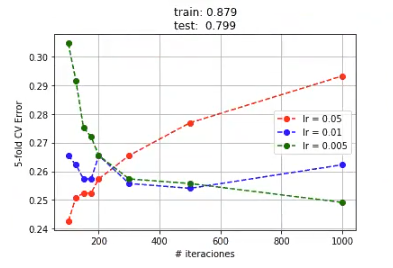
Ahora que has visto, por medio de un ejercicio de boosted trees, su funcionamiento, puedes dar el siguiente paso. Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que aprenderás toda la fundamentación teórica y práctica para cumplir tu sueño e incursionar en el mercado laboral del Big Data. ¡Anímate a transformar tu vida y solicita más información!











