Ejercicio práctico de transformación de variables con R

En este post veremos un ejercicio práctico de transformación de variables con R por medio de un ejemplo con el hormigón.

Desarrollo de ejercicio práctico de transformación de variables con R

In [58]: concrete <- read.csv ("data/Concrete_Data.csv",
col.names = c ("cemento", "escoria", "cenizas", "agua", "plastificante", "aggrueso", "agfino", "edad", "resistencia"))
head (concrete)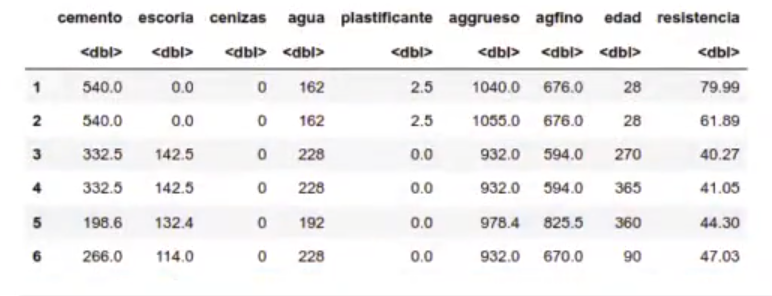

En este ejercicio práctico de transformación de variables con R dividimos entre train y test.

Vamos a calcular un modelo que sea la resistencia, el cemento, la escoria, las cenizas, el agua, el plastificante, el ag. grueso, el ag. fino y la edad.

In [59]: set.seed(123)
idx <- sample (1:nrow (concrete), nrow (concrete) * 0.7)
concrete_train.df <- concrete [idx, ]
concrete_test.df <- concrete [- idx, ]

In [60] : #model_concrete <- lm (resistencia ~ cemento + escoria + cenizas + agua + plastificante + aggrueso + agfino + edad, concrete_train.df)
model_concrete <- lm (resistencia ~ cemento + escoria + cenizas + agua + plastificante + aggrueso + agfino + edad, concrete_train.df)
summary(model concrete)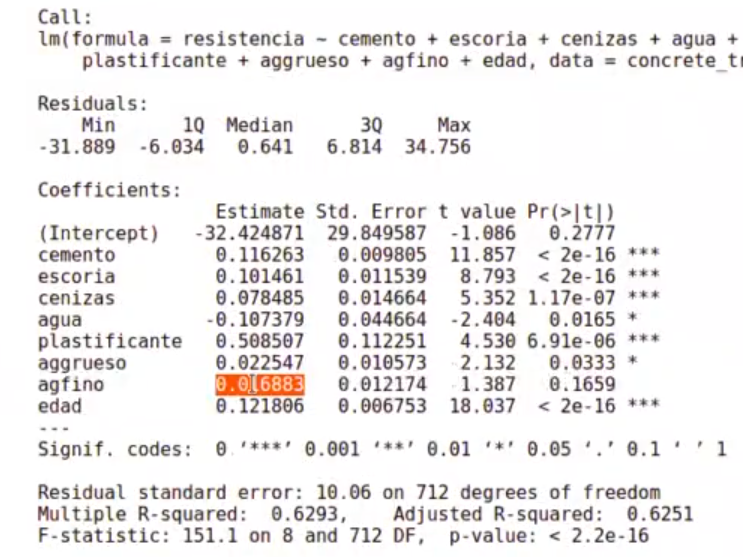

Vamos a aplicar el box cox. Recuerda poner el MASS: :boxcos, en caso de que la librería no haya cargado.

In [61]: bx <- MASS: :boxcox (model_concrete, lambda = seq (-1, 2, length.out = 100))

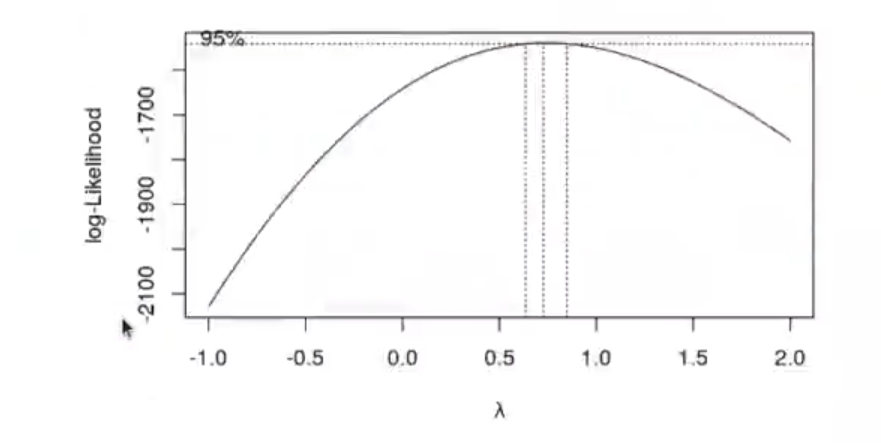
Tenemos otra vez el valor de lambda en la gráfica de nuestro ejercicio práctico de transformación de variables con R.

Creamos dos funciones: la de transformar y la de detransformar.

In (62): l <- bx$x [which.max (bx$y)]
#con esta función transformamos
my_transform <- function (y, l) {
(y ^ l - l) / l
#y con esta detransformamos
my_inv_transform <- function (x, l) {

(x * l + 1) ^ (1 / l)
}
l

0.727272727272727

In [63] : concrete_transformed.train <- concrete_train.df concrete_transformed.train$resistencia_tr <-my_transform (concrete_train.df$resistencia, l)

model_concrete_tre <- lm (resistencia_tr ~ cemento + escoria + cenizas + agua + plastificante + aggrueso + agfino + edad, concrete_transformed.train)
summary (model_concrete_tr)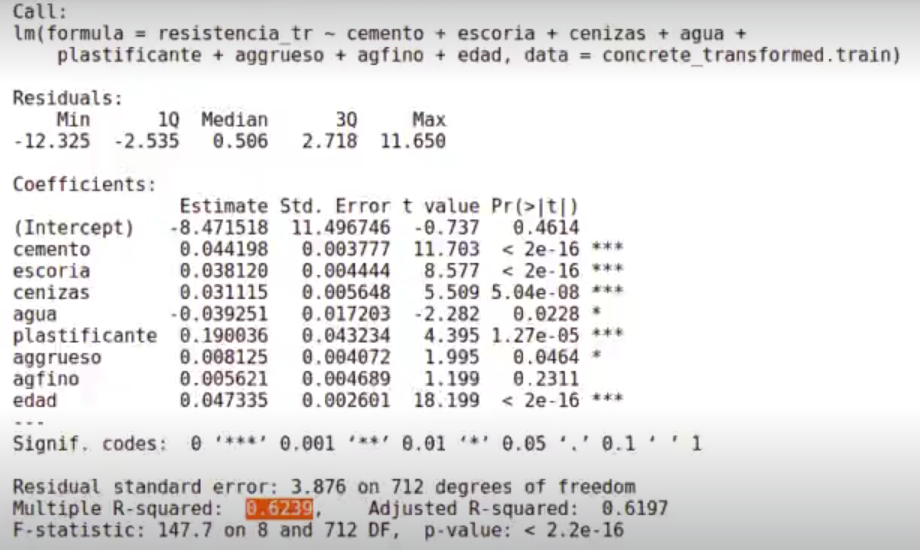

In [64] : par( mfrow = c (1, 2))
qqnorm (y = concrete_transformed.train$resistencia, cex = 0.1) qqline (y = concrete_transformed.train$resistencia, cex = 0.1, col = "red")

qqnorm (y = concrete_transformed.train$resistencia_tr, cex = 0.1)
qqline (y = concrete_transformed.train$resistencia_tr, cex = 0.1, col = "red")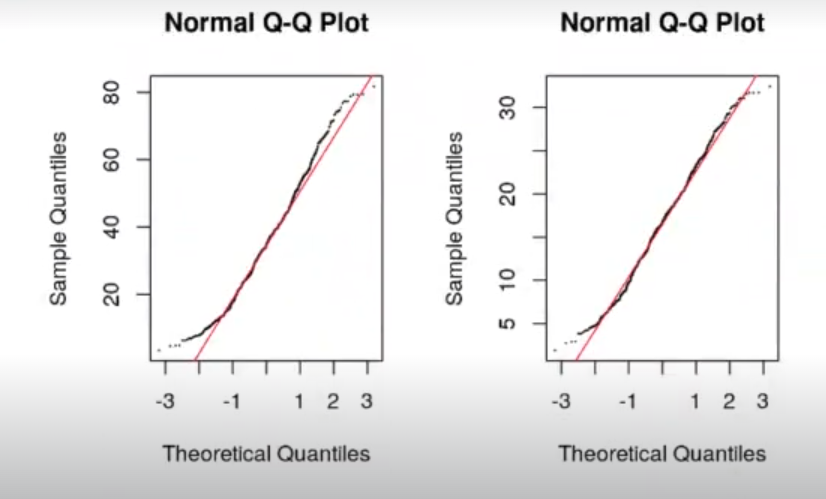

Los datos de los residuos no siguen en absoluto una distribución gaussiana. Los transformados sí siguen este tipo de distribución.

In [65] : par (mfrow = c (1, 2))
qqnorm (y = model_concrete$residuals, cex = 0.1)
qqline (y = model_concrete$residuals, cex = 0.1, col = "red")

qqnorm (y = model_concrete_tr$residuals, cex = 0.1)
qqline (y = model_concrete_tr$residuals, cex = 0.1, col = "red")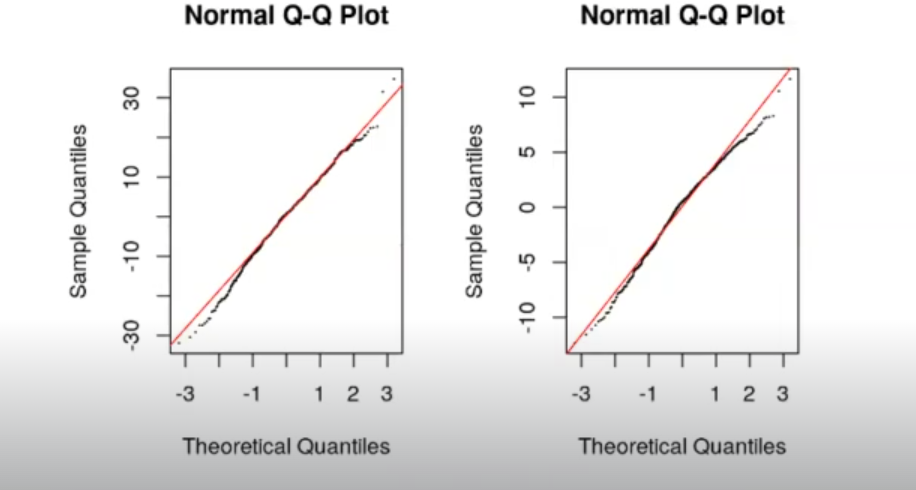

Con los residuos del modelo lo que ocurre es que también los transformados siguen un poco más la distribución gaussiana.

Haremos un modelo para calcular cómo sería el R² con las nuevas muestras de testing:

In [66] : pred_train <- concrete_transformed.train [ , c ("resistencia_tr")]

In [67] : concrete_transformed.test <- concrete_test.df concrete_transformed.test$resistencia_tr <- my_transform (concrete_test.df$resistencia, l)
concrete_transformed.test$pred_tr <- predict (model_concrete_tr, concrete_transformed.test)
concrete_transformed.tests@red <-my_inv_transform (concrete_transformed.test$pred_tr, l)

with (concrete_transformed.test, {

print (caret::postResample (resistencia_tr, pred_tr))
print (caret::postResample (resistencia, pred))
plot (resistencia_tr, resistencia _tr - pred_tr)
plot (resistencia, resistencia - pred)
})

RMSE: 4.2747521

Rsquared: 0.5821341

MAE: 3.4317847

RMSE: 11.6336432

Rsquared: 0.5624026

MAE: 9.1334637

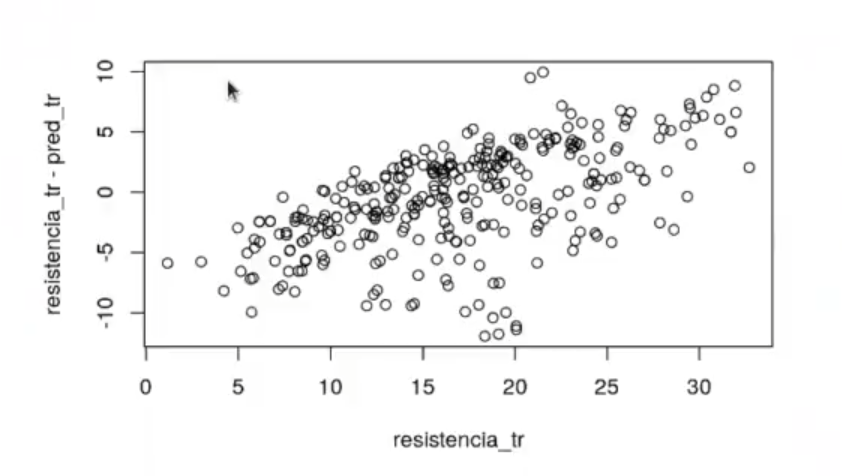
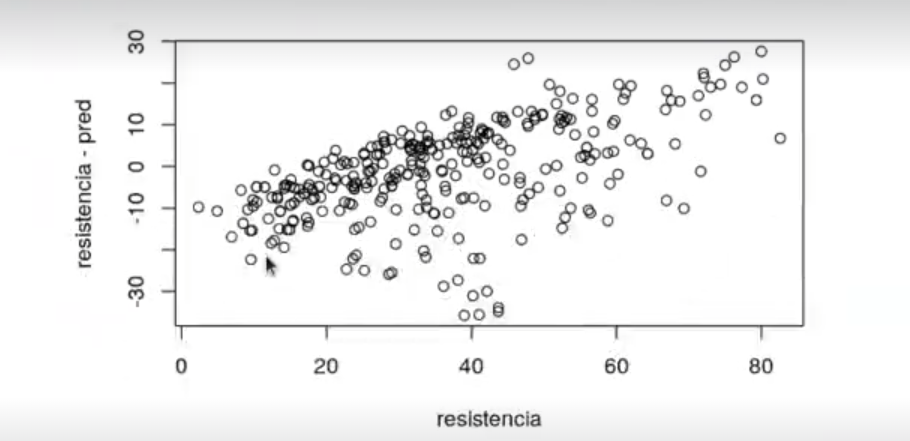
El resultado del ejercicio práctico de transformación de variables con R no cambia mucho, pero sirve para ver cómo funciona este procedimiento.

Ahora que sabes cómo funcionan las transformaciones de variables, puedes seguir aprendiendo gracias a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el que, en muy poco tiempo, podrás aprender todo lo necesario para incursionar en el mercado laboral. ¡Entra y descubre el programa!