Ejercicio sobre espacios vectoriales

En este post resolveremos un ejercicio sobre espacios vectoriales, que consiste en modelar los siguientes prototipos de coches en un espacio vectorial:

Modelo	Precio (€)	Velocidad máxima	Tiempo de aceleración
Porsche Taycan	110000	280 km / h	3.8 s
Tesla3	90000	260 km / h	3.5
BMW i3	60000	160 km / h	7s

Ejercicio sobre espacios vectoriales

Para modelar estos coches a un espacio vectorial debemos crear los vectores correspondientes para cada uno de ellos. ¿Cómo serán dichos vectores si tenemos en cuenta que nuestro espacio vectorial va a ser de 3 dimensiones (precio, velocidad, aceleración)?

Vamos a graficar estos vectores en nuestro espacio vectorial y ver que sucede:

#Ejercicio sobre espacios vectoriales
import numpy as np
from matpltlib import pyplot
from mpl_toolkits.mplot3d import Axes3D
from numpy.random import rand
from pylab import figure

X = np.array ([[110000, 280, 3.8],
[90000, 260, 3.5],
[60000, 160, 7]])

#Ejercicio sobre espacios vectoriales
X.shape

(3, 3)

Definimos un nombre para cada vector para poder visualizarlos:

#Ejercicio sobre espacios vectoriales
y = ['Taycan', 'Tesla', 'i3']

fig = figure ()
ax = Axes3D (fig)

for i in range (len (X)):
      ax.scatter (X [i, 0],
                          X [i, 1],
                          X [i, 2],
                          color = 'b')

     ax.text (X [i, 0],
                   X [i, 1],
                   X [i, 2],
                   f ' {str (y [i])}',
                  size = 20,
                  zorder = 1,
                  color = 'k')

ax.set_xlabel ('precio')
ax.set_ylabel ('velocidad')
ax.set_zlabel ('aceleración')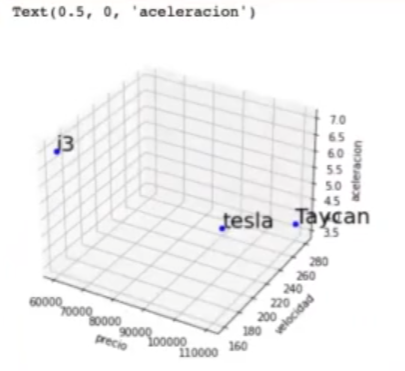

Ya tenemos modelados nuestros coches a un espacio vectorial, en este caso un espacio vectorial de 3 dimensiones.

Ahora, pongamos una situación hipotética: ¿qué sucedería si tenemos más de tres dimensiones? Aquí hemos elegido modelos de estos coches a un espacio vectorial de solo 3 dimensiones para poder representarlo gráficamente. No obstante, normalmente, solemos tener miles de dimensiones/features, en concreto en NLP.

Las dimensiones, por tanto, hacen referencia al número de features que se han elegido para modelar en espacios vectoriales.

Ahora que hemos visto cómo funciona la estructura de un espacio vectorial, puedes seguir aprendiendo sobre Big Data, una de las disciplinas más demandadas hoy en día. Para ello, entra a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación intensiva e íntegra en la que podrás adquirir todos los conocimientos teóricos y prácticos necesarios para entrar en el mercado laboral en poco tiempo. ¡Anímate a impulsar tu carrera laboral y solicita más información!