En este artículo veremos un ejercicio sobre similitud entre vectores, que consiste en comparar dos vectores para ver qué nivel de similitud tienen.
¿Cómo funciona la similitud entre vectores?
Los vectores pueden usarse para representar palabras o incluso frases. Aquí vemos, por ejemplo, un caso en el que podemos representar una palabra usando vectores:
casa = [ 0.50451, 0.68607, -0.59517 -0.022801, 0.60046, -0.13498, -0.08813, 0.47377, -0.61798, -0.31012… 0.78321, -0.91241, -1.6106, -0.64426, -0.51042 ]
Con el uso del producto escalar, podemos calcular la similitud entre dos vectores. Por ejemplo, si convertimos nuestras palabras casa y casita en vectores (empleando un determinado algoritmo) y calculamos el producto escalar de ambos vectores, el resultado debe ser que dichos vectores son muy similares.
En este post vamos a analizar este fenómeno desde el punto de vista del álgebra lineal para entender cómo funciona. Para ello, partimos de la siguiente fórmula:
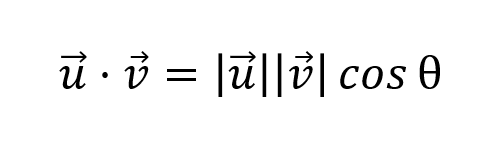
Podemos derivar que la ecuación de similitud viene definida por:
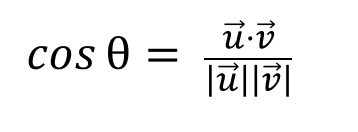
Ejercicio sobre similitud entre vectores
Consideramos los siguientes vectores:
#Ejercicio sobre similitud entre vectores
u = np.array ([1, 2, 3])
v = np.array ([1, 2, 3])La similitud viene definida por el producto escalar u . v entre el producto del módulo de ambos vectores |u||v|.
Una vez definidos los dos vectores u y v, podemos comprobar que, en apariencia, son exactamente iguales. Ahora, vamos a definir la ecuación de similitud necesaria para demostrar que, en efecto, ambos vectores u y v son iguales.
Reemplazaremos valores de la ecuación mostrada anteriormente. Ya sabemos que en la parte de arriba debemos ubicar el producto escalar, que no es más que la suma de los componentes. Asimismo, tenemos claro que en la parte de abajo debemos poner el producto del módulo de u por el módulo de v.
#Ejercicio sobre similitud entre vectores
similarity = (u @ v) / (np.linalg.norm (u) * np.linalg.norm (v))Esto nos da como resultado la similitud entre ambos.
Al ser el vector u igual que el vector v, el cálculo de la similitud nos debe decir que son iguales.
Por lo tanto, si ejecutamos e imprimimos esto, vemos cómo la similitud es igual a 1, lo que significa que ambos vectores, tanto u como v, son exactamente iguales.
#Ejercicio sobre similitud entre vectores
similarity1.0
¿Qué sucede si un vector es completamente distinto, es decir, si va en dirección opuesta? Si le ponemos un poco de lógica al asunto, podríamos pensar que, si es totalmente opuesto el nuevo vector, el resultado debería ser -1.
Vamos a corroborar nuestra hipótesis:
#Ejercicio sobre similitud entre vectores
u = np.array ([-1, -2, -3])
v = np.array ([1, 2, 3])
similarity = (u @ v) / (np.linalg.norm (u) * np.linalg.norm (v))Si copiamos la ecuación de similitud e imprimimos el resultado… En efecto, nos dice que son totalmente opuestos.
#Ejercicio sobre similitud entre vectores
similarity-1.0
La similitud es de -1, tal y como esperábamos.
Lo único que hemos hecho es programar la función de cómo calcular la similitud y poner un ejercicio sobre similitud entre vectores con ejemplos simples de entender.
Función np.linalg.norm de Numpy
La función np.linalg.norm pertenece a la biblioteca numpy de Python. Su función es encontrar el valor de la norma de la matriz o la norma vectorial. Con el parámetro ord se decide si la función encuentra la norma matriz o la norma vectorial.
Algunos de los parámetros de np.linalg.norm son:
- x: es un array que se usa en los procesos de entrada para encontrar el valor de la norma.
- ord: este define el orden de la norma y puede tener diferentes valores, como none, ‘fro’, ‘nuc’, ‘inf’, ‘-inf’, 0, 1, -1, 2, -2, other.
- axis: es un número entero, vacío o una tupla de números enteros.
- keepdims: por defecto está en false; no obstante, si su valor es true, este muestra las dimensiones del eje normalizado.
- n: es la norma de la matriz o vector.
¿Quieres seguir aprendiendo?
Ahora que, gracias a este ejercicio sobre similitud entre vectores, hemos visto cómo funciona, podemos seguir aprendiendo sobre Big Data. Si te gustaría acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que podrás adquirir todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!







