En otro post hemos visto algunas de las generalidades sobre los sistemas de ecuaciones. En esta ocasión, te plantearemos un ejercicio sobre sistemas de ecuaciones y lo resolveremos juntos para que tengas más claridad al respecto.

Ejercicio sobre sistemas de ecuaciones

Existen tres tipos de sistemas de ecuaciones:

Una única solución → sistema compatible determinado
Infinitas soluciones → sistema compatible indeterminado
Sin solución → sistema incompatible

El ejercicio sobre sistemas de ecuaciones que resolveremos aquí está relacionado con el sistema compatible determinado, es decir, el caso en el que las ecuaciones tienen una única solución. Esto significa que el determinante de la matriz A es igual a 0.

Intentaremos resolver el siguiente sistema de ecuaciones:

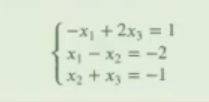
Primero vamos a descomponerlo y a escribirlo como una ecuación matricial de la forma AX = B.

Definimos la matriz A por medio del numpy.array, que va a ser la matriz de transformación. Esta matriz ha salido de la solución al sistema de ecuaciones que hemos planteado previamente. En la primera parte de la primera ecuación tenemos un x₁ (-x₁), en la segunda parte no tenemos componente x₂ (vacío), por tanto, es cero; por último, tenemos un 2x₃, cuyo resultado nos daría 2. Así se ha formado la primera fila de la matriz [-1 0 2].

Ahora continuamos con la segunda fila. Tenemos 1 . x₁ (x₁), que es igual a 1; luego tenemos un -1 . x₂, y no tenemos x₃, de modo que también es cero. Esta fila quedaría como [1, -1, 0].

En la última fila no tenemos x₁, por tanto es cero; tenemos x₂, que es igual a 1, y tenemos x₃, que también es igual a 1. La matriz quedaría como [0, 1, 1].

El vector B sería [1 / -2 / -1]:

#Ejercicio sobre sistemas de ecuaciones
import numpy as np

A = np.array ([[-1,  0,  2],
                         [1,  -1,  0],
                         [0,  1,  1]])

B = np.array ([[1],
                         [-2],
                         [-1]])

print (A)
print (B)

[[-1 0 2]

[1 -1 0]

[0 1 1]]

[[1],

[-2],

[-1]]

Como sabemos que X = A^-1 B, el siguiente paso es calcular la matriz inversa de A:

#Ejercicio sobre sistemas de ecuaciones
#Comprobar si podemos calcular la inversa
np.linalg.det (A)

3.0000000000000004

#Ejercicio sobre sistemas de ecuaciones
A_inv = np.linalg.inv (A)
print (A_inv)

[[-0.33333333 0.66666667 0.66666667]

[-0.33333333 -0.33333333 0.66666667]

[ 0.33333333 0.33333333 0.33333333]]

Multiplicando:

#Ejercicio sobre sistemas de ecuaciones
X = np.dot (A_inv, B)
print ("La solución es: \n", X)

La solución es:

[[-2.33333333]

[-0.33333333]

[-0.66666667]]

#Comprobar si el resultado es correcto

B_hat = np.dot (A, X)
print (B_hat)

[[ 1. ]

[ -2. ]

[ -1. ]]

También podemos resolverlo usando:

#Ejercicio sobre sistemas de ecuaciones
X = np.linalg.solve (A, B)
print (X)

[[-2.33333333]

[-0.33333333]

[-0.66666667]]

Hemos podido calcular la inversa de A porque es cuadrada y el determinante de A es distinto de 0; en caso contrario, no podríamos haberlo calculado. Podemos comprobar si el determinante de A es distinto de 0:

#Ejercicio sobre sistemas de ecuaciones
det_A = np.linalg.det (A)
print (det_A)

3.0000000000000004

Ahora que hemos visto un ejercicio sobre sistemas de ecuaciones, puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector. Podrás acceder a una de las disciplinas más demandadas y con mejores salarios del mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra e intensiva en la que adquirirás todos los conocimientos, tanto a nivel teórico como práctico, para obtener el trabajo de tus sueños. ¡Entra ya y solicita información!