El arg min en un gradiente descendente cumple una función fundamental, ya que lo que queremos lograr es encontrar los parámetros que hacen mínima la función f (w). Veamos en este post un poco más a fondo cómo funciona el arg min en un gradiente descendente.
El arg min en una gráfica
Tenemos la siguiente expresión:
W’ = (xT x)-2 . XT . y
Ahora vamos a reemplazar los valores. Tenemos X, que es una matriz que viene con datos; y tenemos y, que es otra matriz. Por tanto, tenemos que multiplicar xT . x, luego elevarlo a la inversa ((xT x)-2) y, posteriormente, hacer las operaciones restantes.
Si nosotros tenemos una función f, nuestro objetivo siempre es obtener el punto donde se encuentra ubicado el arg min. El arg min en un gradiente descendente no es más que obtener el mínimo de una función f (x).
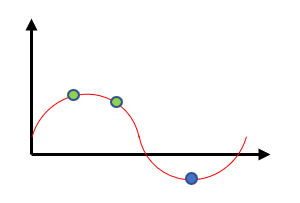
El mínimo de la función es el punto azul en la gráfica. No obstante, los puntos verdes también representan mínimos. Estos últimos se llaman mínimos locales, lo cual indica que, por supuesto, existe un mínimo global, que viene representado por el punto azul.
El mínimo global no es más que el punto más bajo de la ecuación.
Entonces, el gradient descent lo que nos va a permitir es calcular dicho punto, y así es como se ve incluido el arg min en un gradiente descendente.
El arg min en un gradiente descendente
Dibujemos una curva cualquiera:
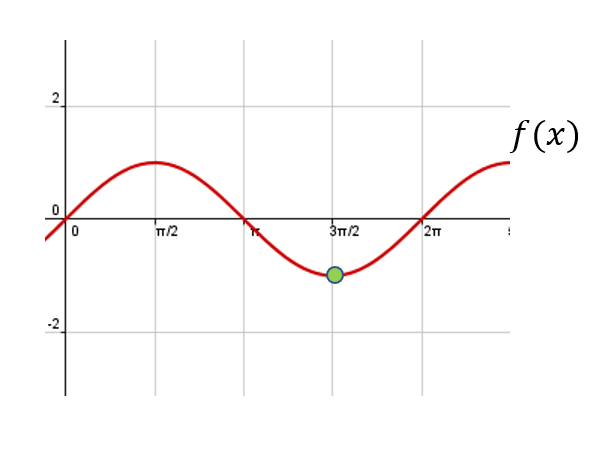
Para entender el arg min en un gradiente descendente, debemos aclarar algunos aspectos.
El mínimo de esta función (es decir, si nosotros hacemos una derivada de esta función respecto a X y la igualamos a 0) nos va a dar el punto que hemos señalado en verde en la gráfica, en el eje y. Pero nosotros no queremos ese valor, queremos el valor que hace la función mínima; ese valor viene dado por arg min en un gradiente descendente.
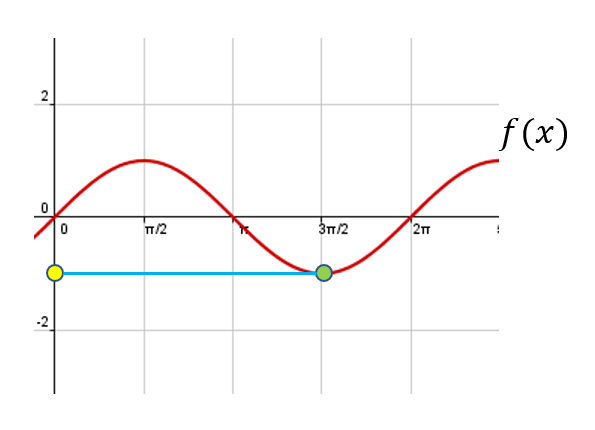
Entonces, min es el mínimo de la función de f (x), pero arg min no es más que el valor de x que nos permite obtener el mínimo, es decir, el valor señalado en la gráfica con el punto amarillo.
La lógica del gradient descent
Dicho esto, vamos a ver la lógica detrás del gradiente.
Supongamos que estamos en la cima de una montaña y queremos descender, pero resulta que queremos descender de la forma más rápida posible. Miramos hacia un lado y vemos que por ahí la velocidad de bajada sería 2; si miramos hacia otro lado, vemos que la velocidad de bajada sería 0.1; si observamos desde otro ángulo, la velocidad sería 1, y desde otro punto sería 0.8. Así pues, el camino que nos permitiría descender lo más rápido posible sería el segundo.
Ahora estamos en un punto más bajo de la montaña y vemos que, por un lado, descenderíamos a una velocidad de 5, por otro a una velocidad de 3, por otro a una velocidad de 1 y por otro a la velocidad de 0.8. Seleccionamos el camino por el que podemos bajar a una velocidad de 5.
Cada una de las decisiones que tomamos se catalogarían como steps. Por tanto, hasta ahora tendríamos dos steps, pero podríamos tener muchísimos más, tantos como necesitemos.
Lo que vemos aquí relacionado con los steps es un proceso iterativo.
De modo que el gradiente de una función f (x) indica una derivada, pero no exactamente la derivada que conocemos generalmente, en donde f (x) = x2. Hace referencia principalmente a funciones que tienen más de una variable. Aquí vemos que la función depende de las variables x e y:
f (x, y) = x2 + 2xy
¿Quieres seguir avanzando?
Ya sabes cómo funciona el arg min en un gradiente descendente, por lo que puedes seguir avanzando en tu proceso de formación. Para poder acceder a las opciones laborales del Big Data, unas de las más prolíficas y mejor pagadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación intensiva e íntegra adquirirás los conocimientos teóricos y prácticos necesarios para obtener el trabajo de tus sueños en pocos meses. ¡No esperes más para impulsar tu carrera y solicita información ahora!











