En este apartado de cálculo en Sympy te mostraremos algunas maneras de manejar Sympy y otras tareas que se pueden hacer con esta librería de Python para matemáticas simbólicas.
El cálculo en Sympy
Suposiciones en Sympy
En todos los programas, creamos un objeto Symbol definiendo una variable como:
x = Symbol (‘x’)
Ejemplo: supongamos que necesitamos comprobar si la expresión x + 5 es mayor que 0:
#cálculo en Sympy
from sympy import Symbol
x = Symbol ('x')
if (x + 5) > 0 :
print ('Ok')
else:
print ('No Ok')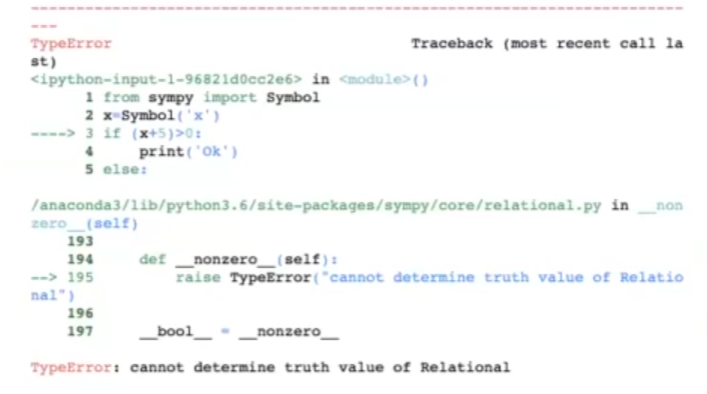
Como Sympy no sabe nada acerca del signo de x, no puede deducir si x + 5 es mayor que 0, por lo que devuelve un error.
#cálculo en Sympy
from sympy import Symbol
x = Symbol ('x', positive = True)
if (x + 5) > 0 :
print ('Ok')
else:
print ('No Ok')Ok
¿Y si lo definiéramos con signo negativo?
from sympy import Symbol
x = Symbol ('x', negative = True)
if (x + 5) > 0 :
print ('Ok')
else:
print ('No Ok')
Nos aparece el mismo mensaje de error que en el anterior cálculo.
Además de poder declarar un symbol como positivo o negativo, también es posible especificar si es real, integer, complex, imaginary y mucho más.
Estas declaraciones es lo que se llaman suposiciones en Sympy.
Límite de funciones
Algo común en este ámbito es calcular el valor al que se aproxima una función. Veamos un ejemplo, en el que consideremos la función 1 / x:
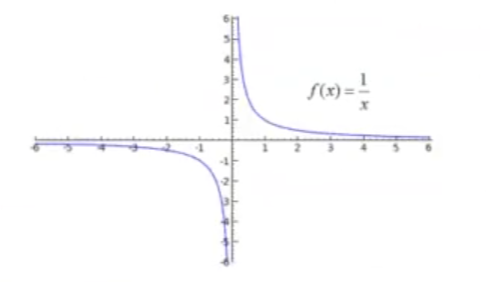
Queremos calcular:
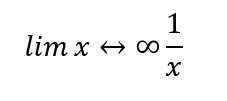
#cálculo en Sympy
from sympy import Limit, Symbol, S
x = Symbol ('x')
l = Limit (1 / x, x, S.Infinity)
lLimit (1 / x, ∞, dir = ‘ – ‘)
l.doit ()0
Por defecto, Limit toma la dirección positiva.
#cálculo en Sympy
from sympy import Limit, Symbol, S
x = Symbol ('x')
l = Limit (1 / x, x, S.Infinity, dir = ' - ')
l.doit ()0
Queremos calcular:
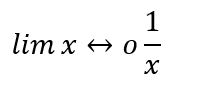
#cálculo en Sympy
from sympy import Limit, Symbol, S
x = Symbol ('x')
l = Limit (1 / x, x, 0)
l.doit ()∞
Limit soporta también indeterminaciones del tipo 0 / 0 y de ∞ / ∞.
Queremos calcular:
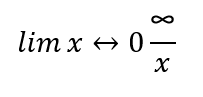
#cálculo en Sympy
from sympy import Limit, Symbol, S
Limit (sin (x) / x, x, 0).doit ()1
No puede faltar hablar del siguiente término, que Bernoulli demostró que tendía a ∅:
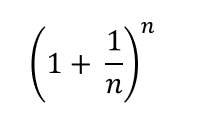
#cálculo en Sympy
from sympy import Limit, Symbol, S
n = Symbol ('n')
Limit ((1 + 1 / n) ** n, n, S.Infinity).doit ()Máximos y mínimos
Los máximos y los mínimos relativos de una función son aquellos que satisfacen f'(x) = 0 y:
- f”(x) > 0 es mínimo
- f”(x) < 0 es máximo
Ejemplo: vamos a calcular los máximos y los mínimos de la función f (x) = x5 – 30x3 + 50x en el dominio [-5, 5]:
#cálculo en Sympy
from sympy import Derivative, Symbol, solve
x = Symbol ('x')
f = x ** 5 + 30 + x ** 3 + 50 * x
d1 = Derivative (f, x).doit ()
puntos_criticos = solve (d1)
puntos_criticos[-I * sqrt (-sqrt (71) + 9),
I * sqrt (-sqrt (71) + 9),
-I * sqrt (-sqrt (71) + 9),
I * sqrt (-sqrt (71) + 9),]
d2 = Derivative (d1, x).doit ()
d220 * x ** 3 + 180 * x
Otra forma de calcular la segunda derivada:
d2 = Derivative (f, x, 2).doit ()
d220 * x * (x ** 2 + 9)
Así no podemos evaluar los puntos en la segunda derivada. Para ello necesitamos crear etiquetas:
A = puntos_criticos [0]
d2.subs ({x : A}).evalf ()-127.661060789073 * I
B = puntos_criticos [1]
d2.subs ({x : B}).evalf ()127.661060789073 * I
C = puntos_criticos [2]
d2.subs ({x : C}).evalf ()703.493179468151 * I
D = puntos_criticos [3]
d2.subs ({x : D}).evalf ()-703.493179468151 * I
Con esto, de hecho, podríamos calcular los máximos y los mínimos relativos. Pero ¡cuidado!, nos faltaría saber qué ocurre en los “bordes” del dominio.
Ahora podrás acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!







