¿Sabes cuál es el papel que juega la hipótesis en una función lineal?
Recordemos que, por un lado, las funciones lineales son aquellas que representan una línea recta en un eje de coordenadas. Por otro lado, una hipótesis, en su acepción más común, es una suposición que se hace a partir de ciertos datos y que sirve como argumento para generar investigaciones de diversas índoles.
Veamos, pues, cómo se ve representada la hipótesis en una función lineal.
¿Dónde se encuentra la hipótesis en una función lineal?
Existen muchas herramientas que nos permiten entender los modelos matemáticos requeridos para realizar procesos de machine learning. Entre estas herramientas se encuentran:
- Los vectores.
- Las matrices.
- Los espacios vectoriales.
- Los eigenvalores y los eigenvectores.
Estos modelos nos sirven para generar las hipótesis. Veamos un ejemplo para entender mejor cómo se relaciona la hipótesis en una función lineal. Supongamos que tenemos el siguiente conjunto de datos:
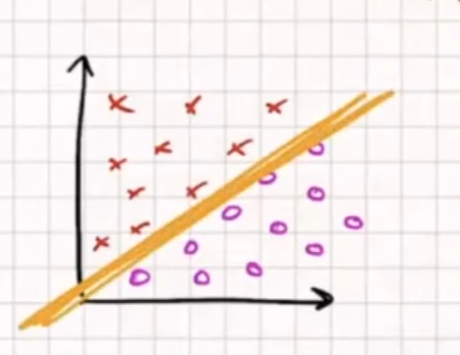
Vemos los datos, los analizamos y llegamos a una conclusión antes de crear un modelo y empezar a hacer pruebas. Podemos pensar que, a lo mejor, una función lineal puede representar nuestros datos; pues bien, lo que estamos haciendo con eso es generar una hipótesis en una función lineal.
La hipótesis sigue la siguiente forma: {wx + b}, donde tenemos los parámetros w y b, que son los que queremos aprender para poder definir la recta y que explique perfectamente nuestros datos.
Cuando hablamos de la hipótesis en una función lineal, lo que estamos queriendo decir es que, cuando tenemos nuestros datos y vemos que tienen la forma que se muestra en la gráfica, podemos creer que una función lineal es la mejor manera para representar los datos o para clasificarlos. De ahí que la forma de la hipótesis en una función lineal sea wx + b, que es la forma de una ecuación lineal.
La cardinalidad de la hipótesis en una función lineal
Como ya sabrás, w y b pueden tomar infinitos valores, cualquier valor en la escala real de números.
Cuando sucede esto, podríamos decir que la cardinalidad (que no es más que el número de elementos que tiene un conjunto) de esa hipótesis en una función lineal (observemos que la hipótesis la estamos representando con llaves, lo que significa que es un set/conjunto) es infinita, es decir: |H| = ∞.
Esta afirmación se debe a lo que hemos comentado anteriormente acerca de los infinitos valores que pueden tomar w y b.
Entonces, esto nos permite llegar a la conclusión de que nuestro modelo puede ser aprendido. ¿Qué significa esto? Se podría resumir en un concepto denominado PAC learnable. Esta es una teoría que existe en el machine learning teórico y dice que, si la cardinalidad de nuestra hipótesis en una función lineal es infinita, nuestro modelo puede ser aprendido.
Un modelo puede ser aprendido
Veamos un ejemplo para entender mejor a qué nos referimos con el hecho de que un modelo puede ser aprendido. Imagina que tenemos un cuadrado que es como el universo, un lienzo, denominémoslo el universal space. El universal space es donde están todas las soluciones posibles. Imaginemos que la mejor solución de nuestro modelo está en algún sector dentro del universal space; esta es la solución más óptima, la más adecuada que podamos encontrar jamás.
Si nuestro modelo es limitado y no tiene cardinalidad infinita, es decir, no puede tomar cualquiera de los valores, indicaría que solo puede tomar un grupo de soluciones dentro del universal space. Por tanto, puede ser que nuestro modelo pueda ser aprendido o no.
En cambio, si la cardinalidad es infinita, nos aseguramos de que la solución óptima para nuestro modelo, representada por la forma h* (h de hipótesis, y el asterisco simboliza que es la mejor) está dentro de las soluciones que puede abarcar nuestra hipótesis en una función lineal.
Por último, debes saber que puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector. Podrás acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra e intensiva de alta calidad en la que adquirirás todos los conocimientos teóricos y prácticos que te ayudarán a obtener tu trabajo soñado. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!







