¿Sabes qué es el perceptrón y cuál es su importancia en el origen de las redes neuronales?
El origen de las redes neuronales viene en intentos de encontrar representaciones matemáticas de procesado de la información en sistemas biológicos.
Frank Rosenblatt y el perceptrón
Aunque la primera implementación de las redes neuronales data de 1947, realmente fue con la aparición del llamado perceptrón, gracias al trabajo de Frank Rosenblatt, en 1956, cuando empezó a coger fama. Incluso la prensa generalista se hizo eco de este hecho: Rival, The New Yorker, 1958.
Plantearon que Rosenblatt definía el perceptrón como el primer objeto no biológico capaz de aprender de su entorno de manera significativa.
Un perceptrón no es más que una regresión lineal con una función de activación a la salida.
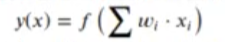
Donde la función de activación f(x) simplemente saca un 1 si el valor está por encima de un umbral o O si está por debajo.
A veces se escribe como:
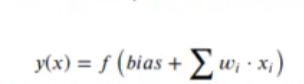
Donde bias es una constante que se añade a la función. Ambas fórmulas son equivalentes si una de las columnas de x se deja como constante.
Se inspira en cómo funciona una neurona del cerebro humano:
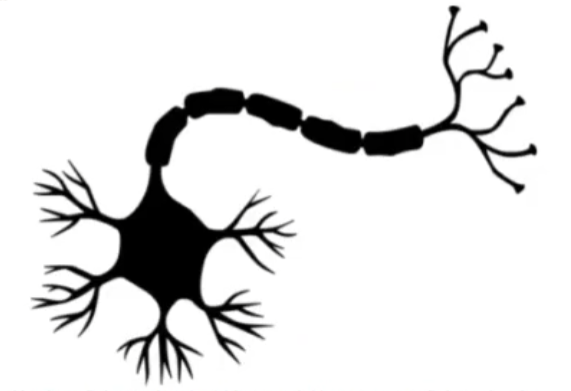
Se supone que una determinada combinación de señales en las dendritas puede lanzar una señal en el axón.
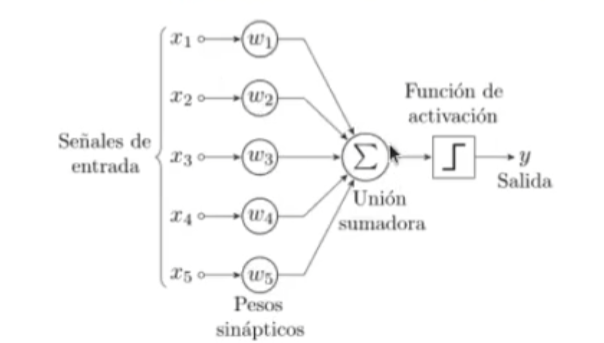
El perceptrón es un clasificador binario que sirve para decir si un vector pertenece o no a una clase.
Ejercicio de aplicación del perceptrón
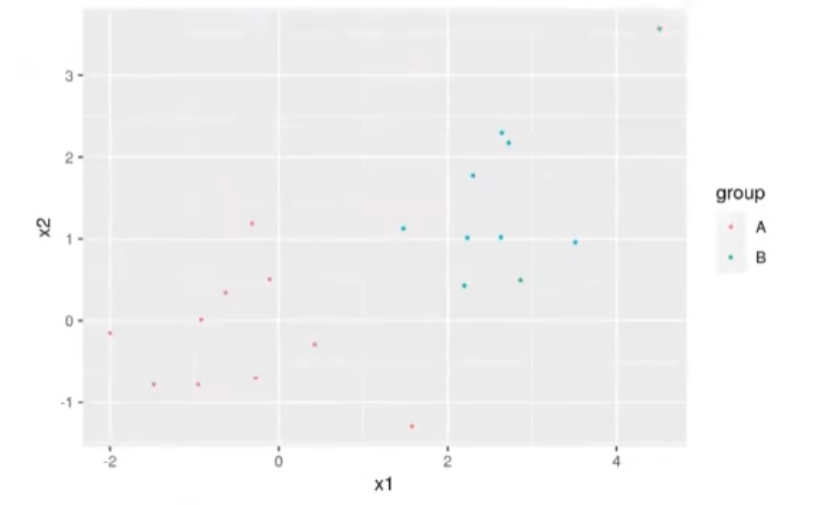
Imaginemos que tenemos dos grupos de datos y queremos diferenciar un valor de otro. Esto se parece un poco a una regresión logística, pero la realidad es que en el entrenamiento esta es un poco más complicada.
options (repr.plot.height = 2, repr.plot.width = 8, repr.plot.res = 200) set.seed (12) Num samples <- 10 dfa <- data.frame (group = "A", x1 = rnorm (Num_samples, mean = 0, sd = 1), x2 = rnorm (Num_samples, mean = 0, sd = 1)) dfb <- data.frame (group = "B", x1 = rnorm (Num_samples, mean = 2.5, sd = 1), x2 = rnorm (Num_samples, mean = 1.5, sd = 1)) df_train <- rbind (dfa, dfb) library (ggplot2) options (repr.plot.height = 4, repr.plot.width = 6) ggplot (df_train, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.5)
La siguiente fórmula sumará los pesos y los multiplicará por cada uno de los coeficientes que se tengan. Si el cálculo resultante es mayor al umbral, devuelve 1; en caso contrario, devolverá 0.
perceptron <- function (x, weigths, threshold = 0) {
if ((weigths [1] + sum (x * weigths [2 : length (weigths)])) > threshold) {
return (1)
}else{
return (0)
}
}
#Comenzaremos con pesos al azar
weigths <- c (1, 1, 1)
threshold <- 0.5
pred <- apply (df_train [ , 2 : 3], 1, function (x) perceptron (x, weigths = weigths, threshold = threshold))
table (factor (pred), df_train$group)
ggplot (df_train, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.5) + geom_abline (slope = -weigths [2] / weigths [3], intercept = (threshold - weigths [1]) / weigths [3], color = 'blue')
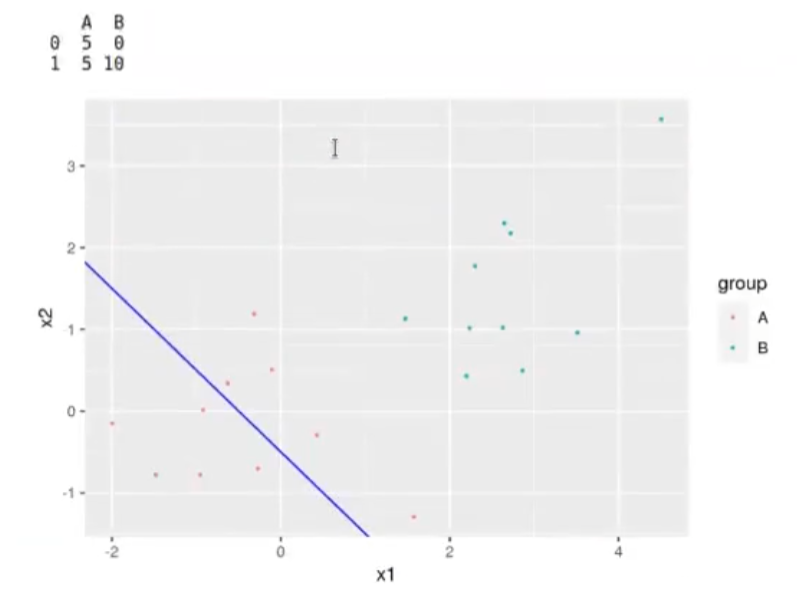
Como observamos, la fórmula ha clasificado mal 5 puntos de A, ya que el umbral los ha puesto en el lado contrario al que deberían ir.
threshold <- 0.5
learning_rate <- 0.002
w <- c (0.5, 0, 0.005)
i <- 0
iter <- 8
i <- 1 %% (nrow (df_train) -1) + 1
iter <- iter + 1
x_vector <- df_train [i, c (2 : 3)]
y_out <- perceptron (x_vector, weigths = w, threshold = threshold)
error = as.numeric (df_train [1, "group"] == "B") -y_out
pre_w <- w
if (error != 0) {
w [1] <- w [1] + error * learning_rate
for (idx in 1 : length (x_vector)) {
w [idx + 1] <- w [idx + 1] + x_vector (1, idx] * error * learning_rate
}
}
paste ("Iteracción", iter, "Dato:", i, "Error:", error, "Pesos:", paste (w, collapse = " , "))
ggplot (df_train, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.5) +
geom_point (size = 3, x = x_vector [1, 1], y = x_vector [1, 2], shape = 0, color = "red") +
geom_abline (slope = -pre_w [2] / pre_w [3], intercept = (threshold - pre_w [1]) / pre_w [3], color = "blue", linetype = 3)+
geom_abline (slope = w [2] / w [3], intercept = (threshold - w [1]) / w [3], color = 'blue')
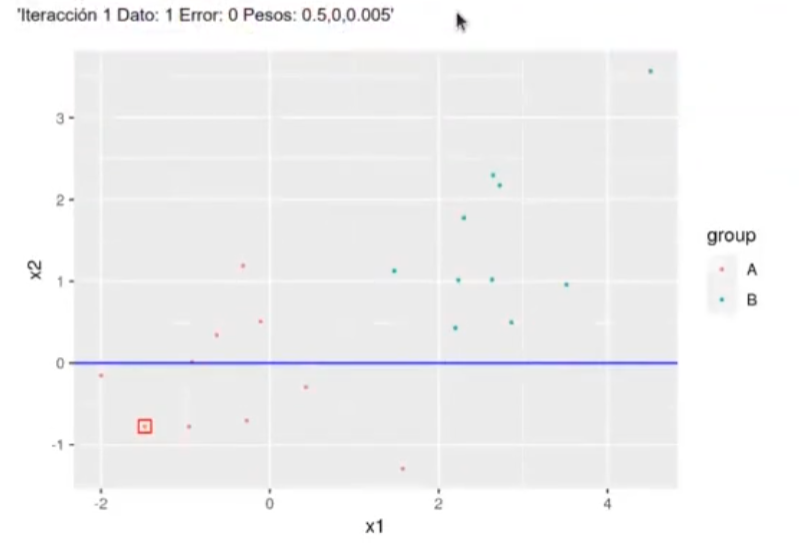
Mientras el algoritmo lo haga bien, no aprende; aprende en el momento en el que se equivoca e intenta corregir.
Si bien este algoritmo era muy sencillo computacionalmente, se puede conseguir grandes logros con él. Por ejemplo, podemos reconocer caracteres numéricos escritos a mano.
Gracias a Rosenblatt iniciaron algunos estudios correspondientes a las redes neuronales, las mismas que tú también puedes seguir estudiando gracias a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Se trata de una formación intensiva en la que aprenderás todo lo necesario para incursionar rápidamente en el mercado laboral IT, conocido por ser el más prolífico y lleno de oportunidades con una alta remuneración económica. ¿Te gustaría cambiar tu vida? ¡Solicita más información y sigue formándote para destacar en el mundillo tecnológico!











