En este post veremos cómo entrenar un árbol de decisión individual. Recordemos que los árboles de decisión son estructuras que nos ayudan muchísimo en problemas de clasificación y en predicciones no temporales. Existen varios tipos de árboles de decisión, como son los árboles de clasificación y los árboles de regresión.
La gran ventaja de los árboles de decisión radica en su extrema simplicidad para ser interpretados. Se podría decir que no existe una estructura más fácil de entender que un árbol de decisión. Por eso, a continuación veremos cómo entrenar un árbol de decisión en tus ejercicios.
Entrenar un árbol de decisión: ejercicio
#Entrenar un árbol de decisión
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
maxDepth = range (1, 10)
param_grid = ('max depth': maxDepth }
grid = GridSearchCV (DecisionTreeClassifier (random_state = 0), param_grid = param_grid, cv = 10)
grid.fit (x_train, y_train)
print ("best mean cross-validation score: { : . 3f}".format (grid.best_score_))
print ("best parameters: {}".format (grid.best_params))
#Entrenar un árbol de decisión
scores = np.array (grid.cv_results ['mean_test_score'])
plt.plot (maxDepth, scores, '-o')
plt.xlabel ('max_depth, fontsize = 16)
plt.ylabel ('10-Fold MSE')
#plt.ylim ((-1, 0))
plt.show ()best mean cross – validation score: 0.941
best parameters: {‘max_depth’: 5}
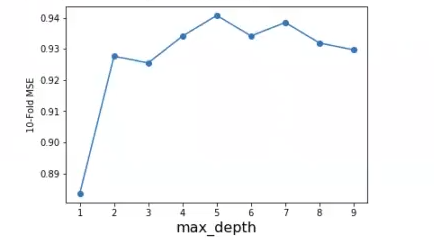
Vemos que el max_depth es igual a 5 en el resultado. No obstante, teniendo en cuenta que la mejora en el accuracy es de tan solo un 1% (de hecho un poquitín menos), es innecesariamente complejo (y más con un dataset tan pequeño) ir hasta 5.
Por esta razón, el max depth óptimo lo llevaremos hasta 2, que es el punto en el que la curva empieza, más o menos, a estabilizarse. Este proceso de llevar el max depth hasta 2, en vez de llevarlo hasta 5, nos ahorrará muchísimo tiempo de procesado y dinero, teniendo en cuenta que tendremos que consumir menos recursos durante menos tiempo para que el algoritmo nos muestre un resultado. Además de eso, observamos que llevarlo hasta 5 sería complicarnos muchísimo la vida, ya que a partir de 2 no sabríamos muy bien cuál es el punto óptimo, porque la gráfica empieza a desestabilizarse.
#Entrenar un árbol de decisión
#maxDepthOptimo = grid.best_params ['max_depth']
maxDepthOptimo = 2
treeModel = DecisionTreeClassifier (max_depth = maxDepthOptimo).fit (x_train, y_train)
print ("Train: ", treeModel.score (X_train, y_train))
print ("Test: ", treeModel.score (X_test, y_test))Train: 0.9516483516483516
Test: 0.9649122807017544
Observemos, por simple curiosidad, qué pasa si dejamos el max depth óptimo en 5, como nos indica la primera gráfica que lo hagamos:
Train: 0.989010989010989
Test: 0.9473684210526315
Con este resultado vemos cómo tendríamos mucho mejor resultado en train, que llega casi a 0.99, y en test estamos en un 0.94, dos puntos más que con un max depth óptimo de 2.
Con el 2 lo que obtenemos son unos resultados más bajos en train, menos ajustados a los datos de entrenamiento, aunque siguen siendo mejores en test.
Es extraño que ocurra que los datos en test son mejores que en train, al final esto es un dataset pequeño y puede haber anomalías; no es del todo normal.
Lo que importa aquí es que hemos mejorado los resultados del test, porque este modelo está generalizando mejor. Así pues, en este caso en concreto, aunque el óptimo sea 5, es mejor irnos hasta 2.
Si tuviéramos un dataset más grande, a lo mejor sí requeriríamos subir el max depth óptimo. La idea es que, cuanto mayor tamaño tenga el conjunto de datos, mayor será la profundidad que se requiera. Al final, debemos tener en cuenta que si, por ejemplo, tenemos que estar clasificando 15 mil instancias, es entendible que necesites una complejidad mayor que si vas a clasificar 100.
Por último, lo que haremos será pintar el árbol:
#Entrenar un árbol de decisión
from sklearn.tree import export_graphviz
import graphviz
tree_dot = export_graphviz (treeModel, out_file = None, feature_names = features, class_names = ['B', 'M'], filled = True, rounded = True, special_characters = True)
graph = graphviz.Source (tree_dot)
graph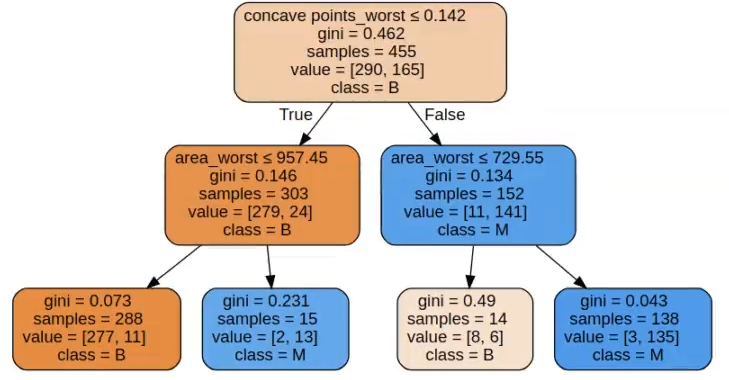
Como podemos observar, es un árbol bastante sencillo, porque el óptimo solo llega hasta 2.
Entrenar un árbol de decisión individual puede ser una tarea fácil, pero solo si sabemos qué estamos haciendo y por qué lo hacemos. Por eso, si quieres crecer en tu camino como data scientist, es importante que entiendas cómo entrenar un árbol de decisión y otros asuntos relacionados con el mundo del Big Data.
Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todas las herramientas teóricas y prácticas para incursionar en este mundo laboral, que está lleno de oportunidades. ¡Anímate a transformar tu vida y solicita ya más información!











