Entrenar un modelo Ridge para distintos valores de α

En este artículo vamos a aprender cómo entrenar un modelo Ridge que tenga distintos valores de α.

Entrenar un modelo Ridge

Lo primero que haremos ahora es representar el valor de los coeficientes del modelo y su norma para distintos valores del parámetro de regularización.

Haremos un np.logspace con 20 valores entre -10 y -3. El np.logspace lo que hace es darnos valores idénticamente distribuidos. Empieza con el primero que le digamos, que es 10 – 10, y acaba con el último.

Entre medias hay otros 18 valores que están idénticamente separados.

#entrenar un modelo Ridge
n_alphas = 20
alphas = np.logspace (-10, -3, n_alphas)
alphas

array ([1.00000000e-10, 2.33572147e-10, 5.45559478e-10, 1.27427499e-09, 2.97635144e-09, 6.95192796e-09, 1.62377674e-08, 3.79269019e-08, 8.85866799e-08, 2.06913888e-07, 4.83293824e-07, 1.12883789e-06, 2.63665098e-06, 6.15848211e-06, 1.43844989e-05, 3.359818290-05, 7.84759976e-05, 1.83298071e-04, 4,28133240e-04, 1.00000000e-03])

#entrenar un modelo Ridge
n_alphas = 20
alphas = np.logspace (-10, -3, n_alphas)

coefs = [ ]

norm2_coefs = [ ]
for a in alphas:
ridge = Ridge (alpha = a).fit (x_train, y_train)
coefs.append (ridge.coef_)
norm2_coefs.append (np.dot (ridge.coef_,ridge.coef_.T))

#Display results
plt.figure (figsize = (14, 5))

ax = plt.subplot (1, 2, 1)
ax.plot (alphas, coefs)
ax.set_xscale ('log')
ax.set_xlim (ax.get_xlim () [ : : - 1]) #reverse axis 
plt.xlabel ('alpha')
plt.ylabel ('$w_i$')
plt.title ('Coeficientes en función de la regularización')
plt.axis ('tight')

#entrenar un modelo Ridge
ax = plt.subplot (1, 2, 2)
ax.plot (alphas, norm2_coefs)
ax.set_xscale ('log')
ax.set_xlim (ax.get_xlim () [ : : - 1]) # reverse axis
plt.xlabel ('alpha')
plt.ylabel('$ l l \mathbf {w} || ^ 2_2$')
plt.title('Norma de los coeffs en función de la regularización')
plt.axis('tight')
plt.show()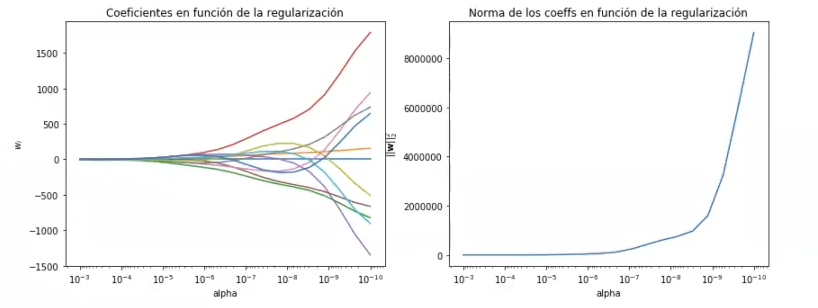

Como podemos observar, la norma de los coeficientes empieza siendo muy alta, debido a que no hay regularización; pero en seguida va bajando hasta que tiende a 0.

Con los coeficientes pasa algo similar, porque todos terminan juntándose en 0.

¿Cuál es el valor óptimo de α? Para responder a este ejercicio de forma correcta, debemos probar con distintos valores de α a partir de los datos, pero ¿cómo calculamos este valor? De nuevo, acudimos a la validación cruzada.

from sklearn.model_selection import GridSearchCV

#entrenar un modelo Ridge
#Por convención, GridSearchCV siempre intenta MAXIMIZAR los resultados, por lo que
#funciones de coste, como MSE, tienen que ir negadas: https://github.com/scikit-learn/scikit-learn/issues/2439
#Por eso aparece neg mean squared error y por eso hay luego un -1 multiplicando

alpha_vector= np. logspace (-15, 1, 25)
param grid = {'alpha': alpha_vector }
grid.fit (x_train, y_train)
grid = GridSearchCV (Ridge (), scoring = 'neg_mean_squared_error', param grid = param_grid, cv = 5)
print ("best mean cross-validation score: { : .3f}".format (grid.best_score_))
print ("best parameters: { }".format (grid.best_params))

scores = -1 * np.array (grid.cv_results_ ['mean_test_score'])
plt.semilogx (alpha_vector, scores, ' -o')
plt.xlabel ('alpha', fontsize = 16)
plt.ylabel ('5 - Fold MSE')
#plt.ylim ((0, 1))
plt.show ()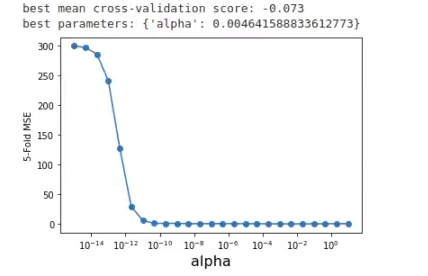

Ahora mismo, con este resultado, no hay manera de ver cuál es el óptimo. Dice en el resultado que el óptimo es 0.004 y nos toca creerlo, porque hasta el momento es lo único que tenemos, no podemos observar nada más.

Lo que podemos hacer es limitar el gráfico entre 0 y 1, en vez de entre 0 y 300, como estamos ahora, y ver qué pasa.

Si descomentariamos la línea #plt.ylim ((0, 1)), nos quedaría algo así:

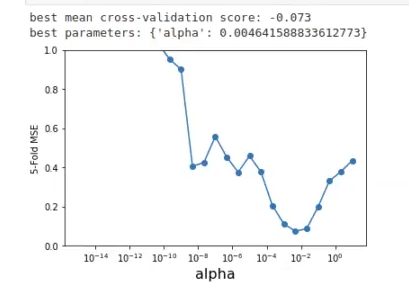
Ahora aquí sí que podemos ver cómo el mejor parámetro parece estar cerca de 0.004.

Entrenamos el modelo con el valor óptimo de α que hemos encontrado con validación cruzada:

#entrenar un modelo Ridge
#Validamos el valor óptimo de alfa
alpha_optimo = grid.best_params_['alpha']
alpha_optimo

0.004641588833612773

A continuación, lo que hacemos es instanciar un modelo Ridge con un alfa óptimo, entrenar el modelo con x_train y train y luego hacer el predict en test:

#entrenar un modelo Ridge
alpha_optimo = grid.best_params_['alpha']
ridge = Ridge (alpha = alpha_optimo).fit (x_train, y_train)

#predicción
y_hat = ridge.predict (X_test)
w = ridge.coef
norm_v2 = np.dot (w, w.T)

#entrenar un modelo Ridge
#error
error test = np.mean (np.powerly = y_hat, 2))

plt.plot (x, g_x, 'r', label = '$y$')
plt.plot (x_i, y_i, 'b.', label = '$y_i$')
plt.plot (x, y_hat, 'g', label = '$\hat {y} s') 
plt.title ('Grado: %i, MSE: %.2f\nalpha: %g, $ | | w l |_2  ^ 2$ = %.2g'% (degree, error_test, alpha_optimo, norm_w2))
plt.legend ()
plt.xlim ((0, 1))
plt.ylim ((-2, 2))
plt.show ()

coef names ['w' + str (i) + ' :  ' for i in range (1, degree + 1)]

for f, wi in zip (coef_names, w):
print (f, wi)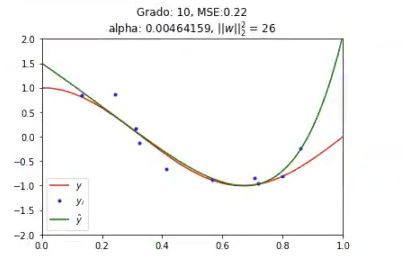

w1: 0.0

w2: -4.224224648792861

w3: -1.224470778992515

w4: 0.8388257771493457

w5: 1.4439115639264841

W6: 1.3230501118147782

W7:0.9869047368946191

W8: 0.9869847368946191

W9: 0.40914806015505434

w10: 0.23984510863439068

Ya vemos cómo hemos conseguido que un modelo muy complejo que tiene 10 grados se regularice de tal manera que se ajusta de una forma bastante buena a los datos que tenemos.

Si quieres seguir aprendiendo sobre Big Data y convertirte en un profesional en uno de los mejores mercados laborales del sector IT, te invitamos a realizar el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de solo 8 meses de duración en la que adquirirás todos los conocimientos y herramientas teóricas y prácticas necesarias para incursionar en este mundillo. ¡Anímate a impulsar tu carrera y solicita más información ahora!