Cuestiones como la la entropía cruzada en Deep Learning forman parte de los facilitadores en este amplio campo del manejo de los macrodatos. De manera que contar con este tipo de saber te ayudará en el procesamiento del Big Data.
Por este motivo, en este post, te explicamos qué es la entropía cruzada en Deep Learning.
¿Qué es la entropía cruzada en Deep Learning?
Para definir qué es la entropía cruzada en Deep Learning, vamos a tratar de entender primero la entropía Python con unos ejemplos.
Primer ejemplo de la entropía cruzada
Para el primer ejemplo de la entropía machine learning, imagina que estamos jugando a un juego en el que tenemos una bolsa con bolas de diferentes colores. La meta del juego es adivinar de qué color es la que un voluntario extrae con el mínimo número de preguntas.
En este caso, tenemos una bola azul, una roja, una verde y una naranja:

Con lo cual, cada bola tiene 1/4 de probabilidades de salir.
Una de las mejores estrategias sería preguntar: primero, si la bola que ha sacado es azul o roja. En caso positivo, preguntaríamos si la bola es azul. En caso negativo, preguntaríamos si es verde. Así que para la entropía Python necesitamos dos preguntas:
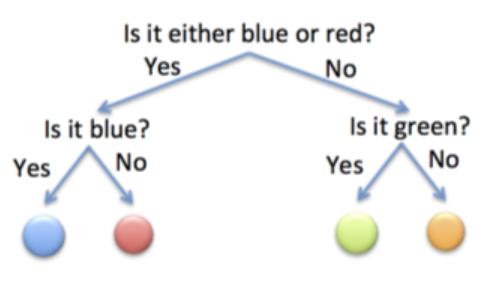
Segundo ejemplo de la entropía cruzada
Esta vez tenemos una bolsa con bolas en las que 12 son azules, 14 son rojas, 18 verdes y 18 rojas. Ahora, la estrategia óptima sería preguntar primero si es azul, ya que hay más probabilidades de que salga una azul.
Si lo es, ya hemos terminado. Si no, podríamos preguntar si es roja, que es la siguiente clase más probable. Si lo fuese, listo. Si no, podríamos preguntar si es verde (o si es naranja).
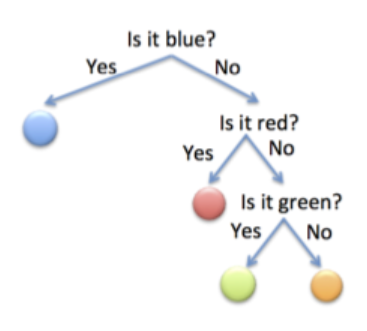
Ahora lo que pasa es que la mitad del tiempo (12) es azul, y nos cuesta 1 pregunta adivinarlo. 14 veces es roja, y nos cuesta 2 preguntas. 18 es verde, y nos cuesta 3 preguntas (lo mismo si es naranja).
Por lo tanto, el número de preguntas esperado para adivinar una bola es: 12⋅1 (azul) +14⋅2 (roja) +18⋅3 (verde) +18⋅3 (naranja) = 1.75.
Tercer ejemplo de la entropía entropia machine learning
Imagina ahora que tenemos una bolsa llena de bolas azules. ¿Cuántas preguntas necesitamos para averiguar de qué color es la bola que saquen? Ninguna.
De estos ejemplos podemos sacar una expresión que permita calcular el número de preguntas dependiendo de la probabilidad de la bola. Así, una bola con probabilidad p cuesta log21p preguntas.
Por ejemplo, para la bola que tiene p=18, necesitamos n_preg=log2118=3
Así que el número de preguntas esperado en total es: n_preg_total=∑ipi⋅log21pi
Al final, una forma de entender la entropía es la siguiente: si siguiéramos la estrategia óptima, ¿cuál es el número esperado de preguntas que nos permitirían adivinar el color de la bola? Por tanto, cuanto más complicado es el juego, mayor es la entropia cruzada. En este caso, Ejemplo 1 > Ejemplo 2 > Ejemplo 3.
Ahora que sabemos qué es la entropía Python, vamos a ver qué es la entropía cruzada en Deep Learning (cross-entropy).
Imagina que seguimos la estrategia del primer ejemplo para el segundo ejemplo:
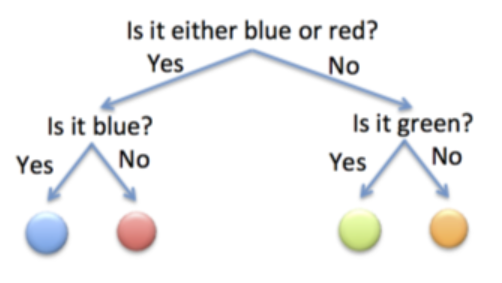
Así, para averiguar si es de cualquier color, hacen falta dos preguntas. Si calculamos el número total de preguntas necesarias, teniendo en cuenta que esta vez cada bola tiene una probabilidad, el resultado es:
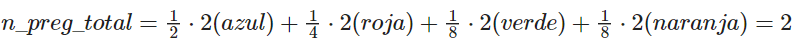
Así que esta estrategia es peor que la estrategia que seguimos en el primer ejemplo. Esto que acabamos de calcular es la entropía cruzada categórica de usar esta estrategia.
Al final, intuitivamente, la entropía machine learning es el número de preguntas esperadas usando la mejor estrategia posible, mientras que la entropía cruzada en Deep Learning es el número de preguntas esperadas cuando no usas la mejor estrategia posible.
Por este motivo, lo que intentamos es minimizar la entropía cruzada.
Formalmente, se define como:
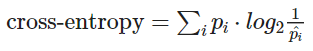
Donde:
- pi es la probabilidad real de las bolas (en nuestro ejemplo, 12 para azul, 14 para rojo, y 18 para verde y naranja).
- pi^ es la probabilidad que hemos asumido al usar nuestra estrategia, que en este caso es que todas las bolas son igual de probables (14 para todos los colores).
Una forma de recordar qué va en cada lugar de la fórmula es tener en mente que queremos averiguar cuántas preguntas hacen falta siguiendo nuestra estrategia, que es pi^, así que dentro del log2 va pi^.
En el desarrollo de este post, te hemos expuesto qué es la entropía cruzada en Deep Learning; sin embargo, esta es una área muy amplia en el manejo de los macrodatos. Por lo que, si planeas profundizar en este campo, necesitas el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. ¡Empieza ahora!







