El valor óptimo de n_neighbors se saca por medio del algoritmo K-NN o k-nearest neighbors, un tipo de algoritmo de aprendizaje supervisado que, a partir de un conjunto de datos determinado, almacena los datos nuevos entrantes en una división de datos similar a la que se ingresa.
¿Qué son los n_neighbors?
Imagina que quieres estudiar un idioma y decides entrar en una academia para aprenderlo. Cuando vas a solicitar información, te dicen que debes hacer un examen de clasificación para ver en qué nivel estás. Resulta que después del examen te dices que eres un A2, por eso te van a poner con personas que tienen más o menos tu mismo nivel.
Básicamente, tus compañeros de clase van a ser tus n_neighbors, lo que se traduciría como n_vecinos, es decir, las personas que van a estar en tu mismo nivel o similar.
En definitiva, los n_neighbors en un algoritmo K-NN son los vecinos más cercanos que tiene un valor cuando ingresa en un conjunto de datos y es clasificado como tal.
¿Cuál es el mejor modo de escoger el valor óptimo de n_neighbors?
En otros artículos ya hemos mencionado que el número de vecinos que escojamos va a afectar muchísimo a las prestaciones del algoritmo, es decir, todas aquellas características que posee, entre las que está el accuracy.
De modo que cuanto más pequeño sea el número de vecinos, más complejo se vuelve el algoritmo y, por tanto, la frontera de separación. Del mismo modo, cuanto más grande sea el número de vecinos, menos compleja se vuelve la frontera.
Cuando el valor óptimo de n_neighbors no está dado en el algoritmo, existe un sobreajuste y, por tanto, empeorará el accuracy. Por el contrario, cuando hay un valor óptimo de n_neighbors, el sobreajuste será menor y mejorará muchísimo el accuracy, pero habrá un punto en el cual ya no podrá mejorar y empezará a caer. Esto es lo que se conoce como underfitting.
De modo que:
- Si los datos de entrenamiento son escasos, el error en test puede ser muy variable, dependiendo de las muestras incluidas en el conjunto de entrenamiento y el conjunto de test.
- Las prestaciones en test dependen del valor óptimo de n_neighbors que determinan la complejidad de la frontera de separación.
Así pues, volvemos a la pregunta: ¿cómo podemos escoger el valor óptimo de n_neighbors?
Selección del modelo: validación cruzada
La validación cruzada (o cross-validation) consiste en subdividir el conjunto de entrenamiento en K partes iguales, de forma que se utilizan K – 1 para entrenar (ajustar el modelo) y el bloque k restante para evaluar las prestaciones en función de los parámetros libres. Este proceso se repite K veces (hasta que se barren todos los bloques) y los resultados se promedian.
Vamos a buscar el valor óptimo de n_neighbors utilizando una estrategia 5-fold CV:
#valor óptimo de n_neighbors
from sklearn.model_selection import StratifiedKFold
X_train, X_test, y_train, y_test = train_test_split (X3, y3, test_size = 0.3, shuffle = True, random_state = 0)
nFolds = 5
kf = StratifiedKFold (n_splits = nFolds, shuffle = True, random_state = 0)
nVecinos = range (1, 16)
j = 0
for n in nVecinos:
knn = KNeighborsClassifier (n_neighbors = n)
i = 0
for idxTrain, idxVal in kf.split (X_train, y_train):
Xt = X_train [idxTrain, :]
yt = y_train [idxTrain]
Xv = X_train [idxVal, :]
yv = y_train [idxVal]
knn.fit (Xt, yt)
accMatriz [i, j] = knn.score (Kv, yv)
i+ = 1
j+ = 1
accVector = np.mean (accMatriz, axis = 0)
accStd = np.std (accMatriz, axis = 0)#valor óptimo de n_neighbors
idx = np.argmax (accVector)
N0pt = nVecinos [idx]
plt.plot (nVecinos, accVector, '-o')
plt.plot (nVecinos [idx], accVector [idx], 'rs')
plt.title ('El número óptimo de vecinos es: %d' % n0pt)
plt.xlabel ('# vecinos')
plt.ylabel ('5-Fold ACC')
plt.grid ()
plt.show ()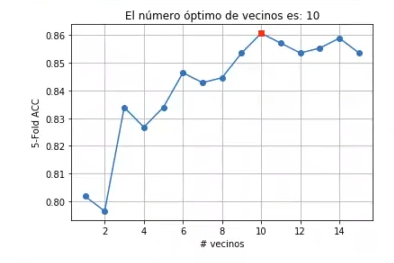
Representemos ahora la gráfica anterior con la variación (desviación estándar) del accuracy en cada fold:
#valor óptimo de n_neighbors
plt.plot (nVecinos, accVector, '-o')
plt.plot (nVecinos [idx], accVector [idx], 'rs')
plt.errorbar (nVecinos, accVector, yerr = accStd, ecolor = 'g')
plt.title ('El número óptimo de vecinos es: %d' % n0pt)
plt.xlabel ('# vecinos')
plt.ylabel ('5-Fold ACC')
plt.grid ()
plt.show ()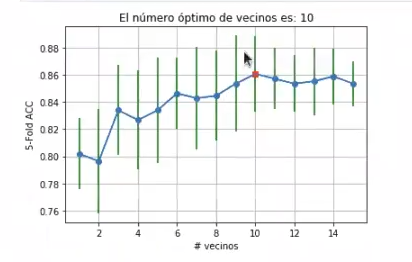
#Damos las prestaciones reales del modelo en test
knn = KNeighborsClassificer (n_neighbors = n0pt)
knn.fit (X_train, y_train)
print ("accuracy: {: . 2f}". format (knn.score (X_test, y_test)))¿Qué sigue?
El mundo del Big Data es tremendamente amplio y quizás en algunas ocasiones te sientas perdido. Si te gustaría dominarlo, no puedes perderte el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, donde encontrarás todas las temáticas que necesitas para convertirte en un profesional que tendrá la posibilidad de acceder a uno de los mercados laborales con mejores posibilidades y mejoras económicas. ¡Anímate a participar en este proceso de aprendizaje y solicita más información ahora!











