¿Alguna vez has escuchado hablar del espacio fila y espacio columna en una matriz? Al igual que existe el espacio nulo, también existen otros espacios, entre ellos el espacio fila y el espacio columna, que están presentes en los ejercicios y procedimientos relacionados con vectores.
El espacio columna, denominado C(A), consiste en todas las combinaciones lineales de las columnas de una matriz A. Estas combinaciones son los posibles vectores Ax. Este espacio es fundamental para resolver la ecuación Ax = b; el sistema Ax = b va a tener solución solamente si b está en el espacio columna de A.
El otro espacio que conforma los espacios importantes de una matriz es el espacio fila, el cual está constituido por las combinaciones lineales de las filas de una matriz.
Espacio fila y espacio columna
Para entender un poco mejor los conceptos de espacio fila y espacio columna, veamos un ejercicio de aplicación para ejemplificar su uso.
Vamos a obtener el espacio columna y el espacio fila para la siguiente matriz:
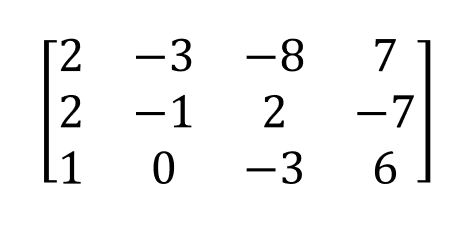
Por tanto, intentaremos resolver la ecuación Ax = b. Para ello, definiremos la matriz de tres dimensiones, donde se tendrán los siguientes valores: (2, -3, -8 7), (-2, -1, 2, -7), (1, 0, -3, 6).
La forma correcta de resolver esto es reduciendo la matriz, es decir, escalonándola. Hay una función, denominada A.rref, que reduce la matriz de tal forma que dentro podamos tener la matriz identidad.
La forma de obtener la matriz identidad es coger la matriz original e intentar hacer operaciones hasta que aparezca dicha matriz.
La matriz identidad es aquella que tiene la diagonal llena de unos (1).
#Ejercicio espacio fila y espacio columna en una matriz
A = sp.Matrix ([[2, -3, -8 7],
[-2, -1, 2, -7],
[1, 0, -3, 6]])
#Reducimos y escalamos la matriz
A.rref ()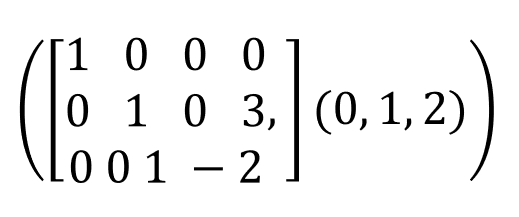
Los números después de la matriz son los pivots o pivotes. Los pivotes nos dicen los primeros elementos de cada fila cuyo valor no es nulo. En este caso, el primer elemento sería el 0, el segundo elemento sería el 1 y el tercer elemento sería el 2.
Hasta ahora no hemos hecho más que reducir y escalonar la matriz automáticamente, es decir, usando Python. Ahora haremos este procedimiento a mano.
Entonces, el espacio columna lo podemos sacar haciendo un bucle. Si imprimimos el resultado, lo que se estarían imprimiendo son los pivotes:
#Ejercicio espacio fila y espacio columna en una matriz
#Espacio columna
for c in A.rref () [1]:
print (c)0
1
2
Lo que vamos a hacer ahora es coger el primer pivot, que es cero, y le vamos a pedir que nos devuelva A [:, c]:
#Ejercicio espacio fila y espacio columna en una matriz
#Espacio columna
for c in A.rref () [1]:
print (A [:, c])Matrix ([[2], [-2], [1]])
Matrix ([[-3], [-1], [0]])
Matrix ([[-8], [2], [-3]])
Lo que vemos como resultado, es decir el A [:, c], es el espacio columna de la matriz A. En este caso sería:
2 -3 -8
-2 -1 0
1 0 -3
Si esto lo hiciéramos de otro modo, el resultado sería:
#Ejercicio espacio fila y espacio columna en una matriz
[A [:, c] for c in A.rref () [1]]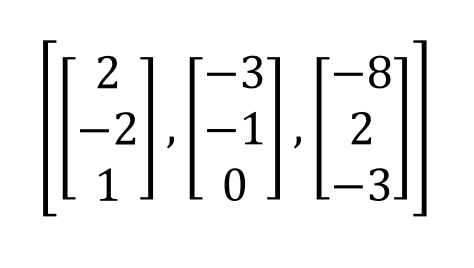
[0, 1, 2] es la ubicación de los pivotes. Los pivotes son los primeros elementos de cada fila cuyo valor es distinto a 0.
Ahora bien, podríamos hacer el mismo procedimiento con el espacio fila, que en vez de coger las columnas, nos coge las filas:
#Ejercicio espacio fila y espacio columna en una matriz
#Espacio fila
for r in A.rref () [1]:
print (r)0
1
2
#Ejercicio espacio fila y espacio columna en una matriz
#Espacio fila
for r in A.rref () [1]:
print (A.rref () [0] [r, :])Matrix ([[1, 0, 0, 0]])
Matrix ([[0, 1, 0, 3]])
Matrix ([[0, 0, 1, -2]])
#Ejercicio espacio fila y espacio columna en una matriz
[A.rref () [0] [r, :] for r in A.rref () [1]][[1 0 0 0], [0 1 0 3], [0 0 1 -2]]
Ya has descubierto cómo funcionan los espacios vectoriales como el espacio fila y espacio columna, por lo que es el momento de ir un paso más allá y continuar aprendiendo sobre el Big Data. Para lograr acceder a una de las disciplinas más demandadas y mejor pagadas del mercado laboral actual, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación intensiva en la que podrás adquirir todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños en menos de un año. ¡Accede ya para solicitar información y anímate a transformar tu futuro!







